Engage NY Eureka Math Geometry Module 1 Lesson 3 Answer Key
Eureka Math Geometry Module 1 Lesson 3 Exercise Answer Key
Opening Exercise
In the following figure, circles have been constructed so that the endpoints of the diameter of each circle coincide with the endpoints of each segment of the equilateral triangle.
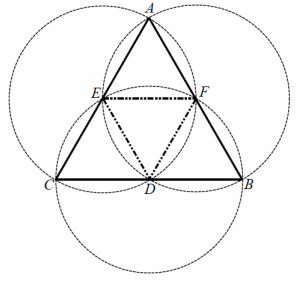
a. What is special about points D, E, and F? Explain how this can be confirmed with the use of a compass.
Answer:
D, E, and F are midpoints. The compass can be adjusted to the length of CE and used to compare to the lengths AE, AF, BF, CD, and BD.
b. Draw \(\overline{D E}\), \(\overline{E F}\), and \(\overline{F D}\). What kind of triangle must △DEF be?
Answer;
△DEF is an equilateral triangle.
c. What is special about the four triangles within △ABC?
Answer:
All four triangles are equilateral triangles of equal side lengths; they are congruent.
d. How many times greater is the area of △ABC than the area of △CDE?
Answer:
The area of △ABC is four times greater than the area of △CDE.
Discussion
Define the terms angle, interior of an angle, and angle bisector.
ANGLE: An angle is the ____.
Answer:
ANGLE: An angle is the union of two noncollinear rays with the same endpoint.
INTERIOR: The interior of ∠BAC is the set of points in the intersection of the half-plane of \(\overleftrightarrow{A C}\) that contains B and the half-plane of \(\overleftrightarrow{A B}\) that contains C. The interior is easy to identify because it is always the “smaller” region of the two regions defined by the angle (the region that is convex). The other region is called the exterior of the angle.
ANGLE BISECTOR: If C is in the interior of ∠AOB, ____. When we say m∠AOC=m∠COB, we mean that the angle measures are equal.
Answer:
ANGLE BISECTOR: If C is in the interior of ∠AOB, and m∠AOC=m∠COB, then \(\overrightarrow{O C}\) bisects ∠AOB, and \(\overrightarrow{O C}\) is called the bisector of ∠AOB. When we say m∠AOC=m∠COB, we mean that the angle measures are equal.
Mathematical Modeling Exercise 1:
Investigate How to Bisect an Angle
You need a compass and a straightedge.
Joey and his brother, Jimmy, are working on making a picture frame as a birthday gift for their mother. Although they have the wooden pieces for the frame, they need to find the angle bisector to accurately fit the edges of the pieces together. Using your compass and straightedge, show how the boys bisected the corner angles of the wooden pieces below to create the finished frame on the right.
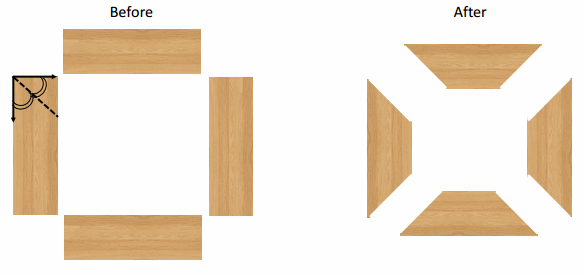
Consider how the use of circles aids the construction of an angle bisector. Be sure to label the construction as it progresses and to include the labels in your steps. Experiment with the angles below to determine the correct steps for the construction.

What steps did you take to bisect an angle? List the steps below:
Answer:
Steps to construct an angle bisector are as follows:
- Label vertex of angle as A.
- Draw circle A: center A, any size radius.
- Label intersections of circle A with rays of angle as B and C.
- Draw circle B: center B, radius BC.
- Draw circle C: center C, radius CB.
- At least one of the two intersection points of circle B and circle C lie in the angle. Label that intersection point D.
- Draw \(\overrightarrow{A D}\).
→ How does the video’s method of the angle bisector construction differ from the class’s method? Are there fundamental differences, or is the video’s method simply an expedited form of the class’s method?
→ Yes, the video’s method is an expedited version with no fundamental difference from the class’s method.
Mathematical Modeling Exercise 2:
Investigate How to Copy an Angle
You need a compass and a straightedge.
You and your partner have been provided with a list of steps (in random order) needed to copy an angle using a compass and straightedge. Your task is to place the steps in the correct order, and then follow the steps to copy the angle below.
Answer:
Steps needed (in correct order):
Steps to copy an angle are as follows:
- Label the vertex of the original angle as B.
- Draw \(\overrightarrow{\boldsymbol{E G}}\) as one side of the angle to be drawn.
- Draw circle B: center B, any radius.
- Label the intersections of circle B with the sides of the angle as A and C.
- Draw circle E: center E, radius BA.
- Label intersection of circle E with \(\overrightarrow{\boldsymbol{E G}}\) as F.
- Draw circle F: center F, radius CA.
- Label either intersection of circle E and circle F as D.
- Draw \(\overrightarrow{\boldsymbol{E D}}\).
Eureka Math Geometry Module 1 Lesson 3 Problem Set Answer Key
Bisect each angle below.
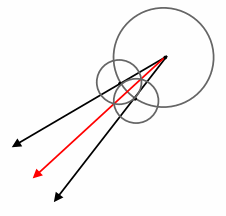
Question 1.
Answer:
Question 2.
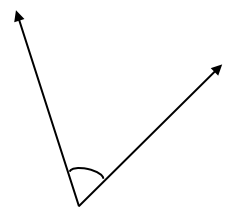
Answer:
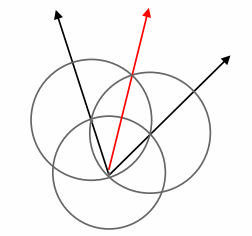
Question 3.
Answer:
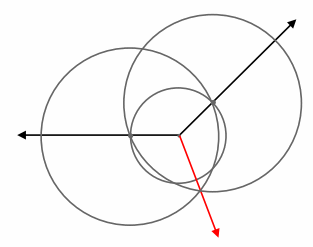
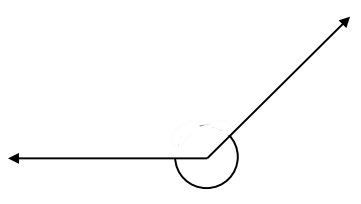
Question 4.

Answer:
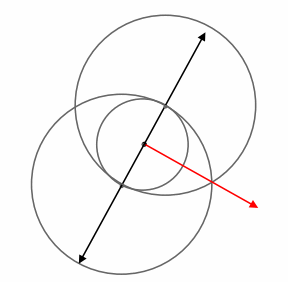
Copy the angle below.
Question 5.
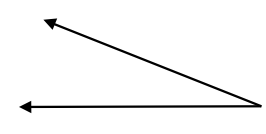
Answer:

Eureka Math Geometry Module 1 Lesson 3 Exit Ticket Answer Key
Later that day, Jimmy and Joey were working together to build a kite with sticks, newspapers, tape, and string. After they fastened the sticks together in the overall shape of the kite, Jimmy looked at the position of the sticks and said that each of the four corners of the kite is bisected; Joey said that they would only be able to bisect the top and bottom angles of the kite. Who is correct? Explain.
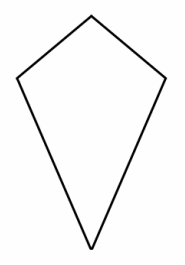
Answer:
Joey is correct. The diagonal that joins the vertices of the angles between the two pairs of congruent sides of a kite also bisects those angles. The diagonal that joins the vertices of the angles created by a pair of the sides of uneven lengths does not bisect those angles.