Engage NY Eureka Math Geometry Module 1 Lesson 22 Answer Key
Eureka Math Geometry Module 1 Lesson 22 Example Answer Key
Example
What if we had the SAS criteria for two triangles that were not distinct? Consider the following two cases. How would the transformations needed to demonstrate congruence change?
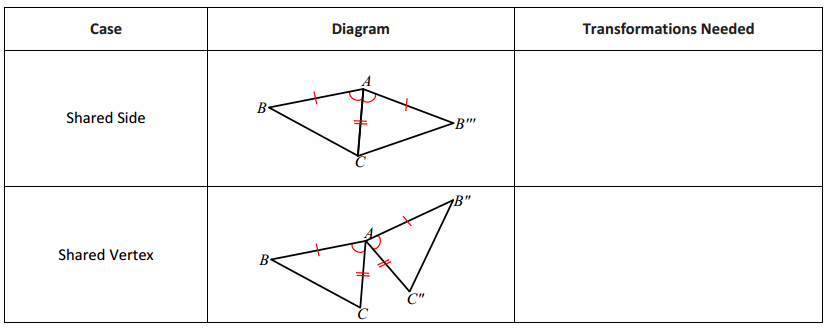
Answer:
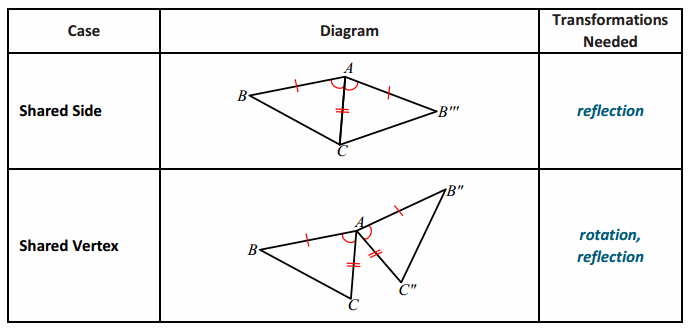
Eureka Math Geometry Module 1 Lesson 22 Exercise Answer Key
Opening Exercise
Answer the following question. Then discuss your answer with a partner.
Do you think it is possible to know whether there is a rigid motion that takes one triangle to another without actually showing the particular rigid motion? Why or why not?
Answer:
Answers may vary. Some students may think it is not possible because it is necessary to show the transformation as proof of its existence. Others may think it is possible by examining the triangles carefully.
It is common for curricula to take indicators of triangle congruence such as SAS and ASA as axiomatic, but this curriculum defines congruence in terms of rigid motions (as defined in the G-CO domain). However, it can be shown that these commonly used statements (SAS, ASA, etc.) follow from this definition of congruence and the properties of basic rigid motions (G-CO.B.8). Thus, these statements are indicators of whether rigid motions exist to take one triangle to the other. In other words, we have agreed to use the word congruent to mean there exists a composition of basic rigid motion of the plane that maps one figure to the other. We see that SAS, ASA, and SSS imply the existence of the rigid motion needed, but precision demands that we explain how and why.
While there are multiple proofs that show that SAS follows from the definition of congruence in terms of rigid motions and the properties of basic rigid motions, the one that appears in this lesson is one of the versions most accessible for students.
Discussion
It is true that we do not need to show the rigid motion to be able to know that there is one. We are going to show that there are criteria that refer to a few parts of the two triangles and a correspondence between them that guarantee congruency (i.e., existence of rigid motion). We start with the Side-Angle-Side (SAS) criteria.
SIDE-ANGLE-SIDE TRIANGLE CONGRUENCE CRITERIA (SAS): Given two triangles △ABC and △A’B’C’ so that AB=A’B’ (Side), m∠A=m∠A’ (Angle), and AC=A’ C’ (Side). Then the triangles are congruent.
The steps below show the most general case for determining a congruence between two triangles that satisfy the SAS criteria. Note that not all steps are needed for every pair of triangles. For example, sometimes the triangles already share a vertex. Sometimes a reflection is needed, sometimes not. It is important to understand that we can always use some or all of the steps below to determine a congruence between the two triangles that satisfies the SAS criteria.
PROOF: Provided the two distinct triangles below, assume AB=A’B’ (Side), m∠A=m∠A’ (Angle), and AC=A’C’ (Side).
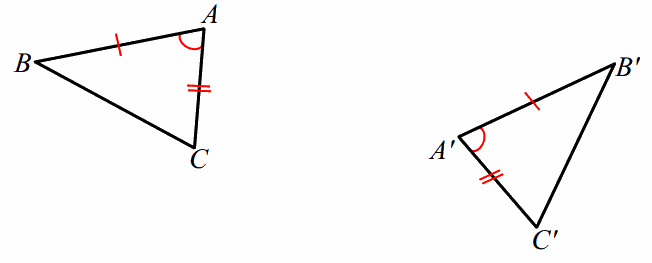
By our definition of congruence, we have to find a composition of rigid motions that maps △A’B’C’ to △ABC. We must find a congruence F so that (△A’B’C’) = △ABC. First, use a translation T to map a common vertex.
Which two points determine the appropriate vector?
Answer:
A’, A
Can any other pair of points be used? Why or why not?
Answer:
No. We use A’ and A because only these angles are congruent by assumption.
State the vector in the picture below that can be used to translate △A’B’C’.
Answer:
\(\overrightarrow{\boldsymbol{A}^{\prime} \boldsymbol{A}}\)
Using a dotted line, draw an intermediate position of △A’B’C’ as it moves along the vector:
Answer:
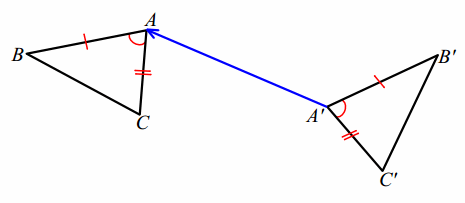
After the translation (below), \(T_{\overrightarrow{A^{\prime} A}}\) (△A’B’C’) shares one vertex with △ABC, A. In fact, we can say
Answer:
\(T_{\overrightarrow{A^{\prime} A}}\) (△A’B’C’ )= △AB”C”.
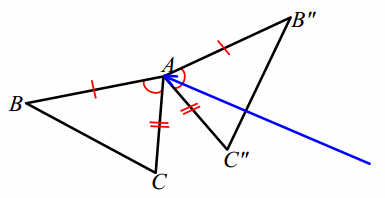
Next, use a clockwise rotation R∠CAC” to bring the side \(\overline{A C”}\) to \(\overline{A C}\) (or a counterclockwise rotation to bring \(\overline{A B”}\) to \(\overline{A B}\) ).
A rotation of appropriate measure maps \(\overrightarrow{A C^{\prime \prime}}\) to \(\overrightarrow{A C}\), but how can we be sure that vertex C” maps to C? Recall that part of our assumption is that the lengths of sides in question are equal, ensuring that the rotation maps C” to C.
(AC=AC”; the translation performed is a rigid motion, and thereby did not alter the length when \(\overline{A C’}\) became \(\overline{A C”}\) .)
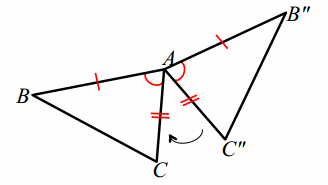
After the rotation R∠CAC”(△AB”C”), a total of two vertices are shared with △ABC, A and C. Therefore,
Answer:
R∠CAC”(△AB”C”)= △AB”’C.
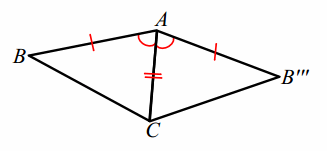
Finally, if B”’ and B are on opposite sides of the line that joins AC, a reflection r\(\overline{A C}\) brings B”’ to the same side as B.
Since a reflection is a rigid motion and it preserves angle measures, we know that m∠B”’ AC=m∠BAC and so \(\overrightarrow{A B^{\prime \prime \prime}}\) maps to \(\overrightarrow{A B}\). If, however, \(\overrightarrow{A B^{\prime \prime \prime}}\) coincides with \(\overrightarrow{A B}\), can we be certain that B”’ actually maps to B? We can, because not only are we certain that the rays coincide but also by our assumption that AB=AB”’. (Our assumption began as AB=A’ B’, but the translation and rotation have preserved this length now as AB”’.) Taken together, these two pieces of information ensure that the reflection over \(\overline{A C}\) brings B”’ to B.
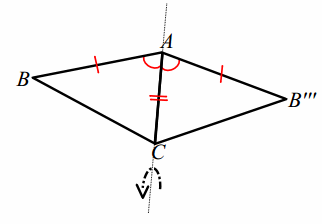
Another way to visually confirm this is to draw the marks of the _____ construction for \(\overline{A C}\).
Answer:
Another way to visually confirm this is to draw the marks of the perpendicular bisector construction for \(\overline{A C}\).
Write the transformations used to correctly notate the congruence (the composition of transformations) that take
△A’ B’ C’≅ △ABC:
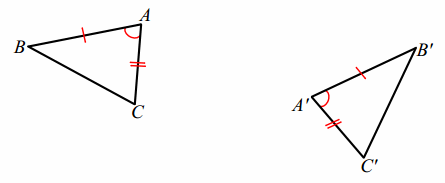
Answer:
F Translation
G Rotation
H Reflection
H(G(F(△A’ B’ C’ ))) = △ABC
We have now shown a sequence of rigid motions that takes △A’B’C’ to △ABC with the use of just three criteria from each triangle: two sides and an included angle. Given any two distinct triangles, we could perform a similar proof.
There is another situation when the triangles are not distinct, where a modified proof is needed to show that the triangles map onto each other. Examine these below. Note that when using the Side-Angle-Side triangle congruence criteria as a reason in a proof, you need only state the congruence and SAS.
Exercises
Exercise 1.
Given: Triangles with a pair of corresponding sides of equal length and a pair of included angles of equal measure. Sketch and label three phases of the sequence of rigid motions that prove the two triangles to be congruent.
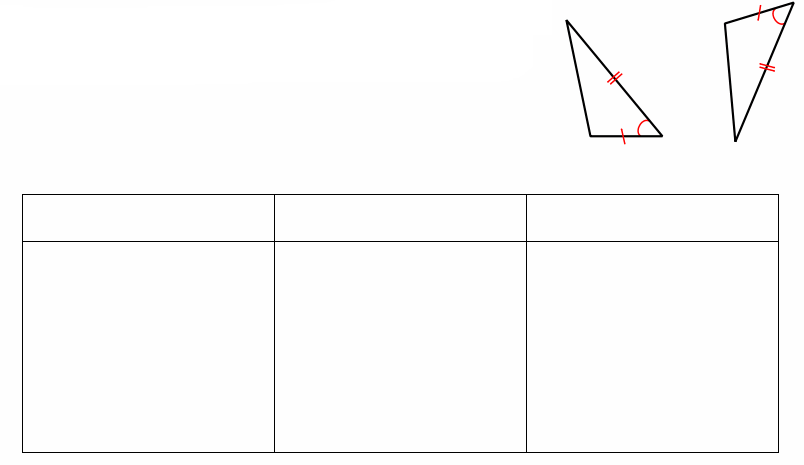
Answer:
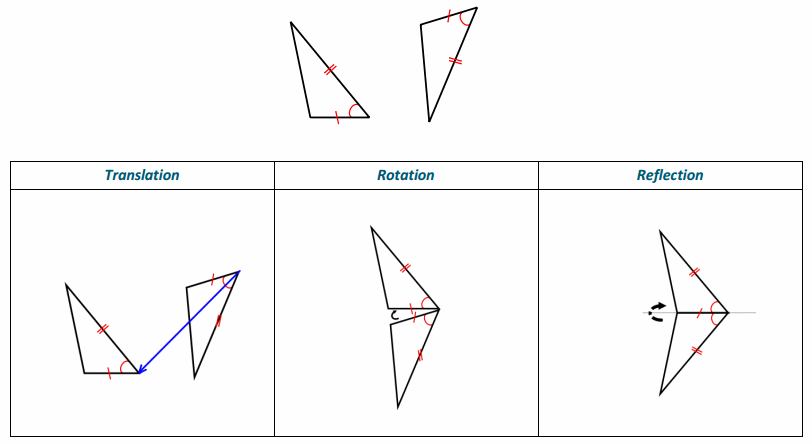
Justify whether the triangles meet the SAS congruence criteria; explicitly state which pairs of sides or angles are congruent and why. If the triangles do meet the SAS congruence criteria, describe the rigid motion(s) that would
map one triangle onto the other.
Exercise 2.
Given: m∠LNM=m∠LNO, MN=ON
Do △LNM and △LNO meet the SAS criteria?
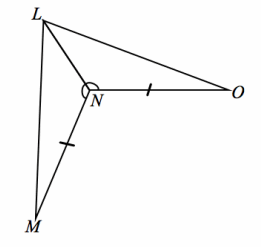
Answer:
m∠LNM=m∠LNO Given
MN=ON Given
LN=LN Reflexive property
△LNM≅△LNO SAS
The triangles map onto one another with a reflection over \(\overline{L N}\) .
Exercise 3.
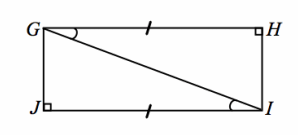
Given: m∠HGI=m∠JIG, HG=JI
Do △HGI and △JIG meet the SAS criteria?
Answer:
m∠HGI=m∠JIG Given
HG=JI Given
GI=IG Reflexive property
△HGI≅△JIG SAS
The triangles map onto one another with a 180° rotation about the midpoint of the diagonal.
Exercise 4.
Is it true that we could also have proved △HGI and △JIG meet the SAS criteria if we had been given that ∠HGI≅∠JIG and \(\overline{\boldsymbol{H G}}\)≅\(\overline{\boldsymbol{J L}}\)? Explain why or why not.
Answer:
Yes, this is true. Whenever angles are equal, they can also be described as congruent. Since rigid motions preserve angle measure, for two angles of equal measure, there always exists a sequence of rigid motions that will carry one onto the other. Additionally, since rigid motions preserve distance, for two segments of equal length, there always exists a sequence of rigid motions that carries one onto the other.
Eureka Math Geometry Module 1 Lesson 22 Problem Set Answer Key
Justify whether the triangles meet the SAS congruence criteria; explicitly state which pairs of sides or angles are congruent and why. If the triangles do meet the SAS congruence criteria, describe the rigid motion(s) that would map one triangle onto the other.
Question 1.
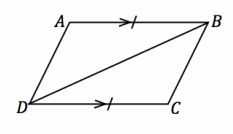
Given: \(\overline{A B}\) || \(\overline{C D}\) , and AB=CD
Do △ABD and △CDB meet the SAS criteria?
Answer:
AB=CD, \(\overline{A B}\) || \(\overline{C D}\) Given
BD=DB Reflexive property
m∠ABC=m∠CDB If a transversal intersects two parallel lines, then the measures of the alternate interior angles are equal in measure.
△ABD≅ △CDB SAS
The triangles map onto one another with a 180° rotation about the midpoint of the diagonal.
Question 2.
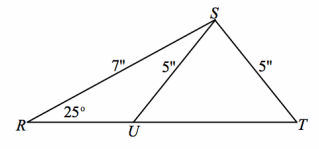
Given: m∠R=25°, RT=7″, SU=5″, and ST=5″ Do △RSU and △RST meet the SAS criteria?
Answer:
There is not enough information given.
Question 3.
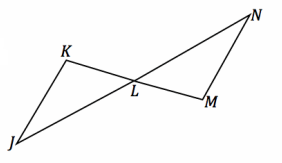
Given: \(\overline{K M}\) and \(\overline{J N}\) bisect each other Do △JKL and △NML meet the SAS criteria?
Answer:
\(\overline{K M}\) and \(\overline{J N}\) bisect each other Given
m∠KLJ=m∠MLN Vertical angles are equal in measure
KL=ML Definition of a segment bisector
JL=NL Definition of a segment bisector
△JKL≅ △NML SAS
The triangles map onto one another with a 180° rotation about L.
Question 4.
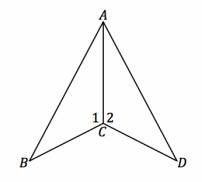
Given: m∠1=m∠2, and BC=DC Do △ABC and △ADC meet the SAS criteria?
Answer:
m∠1=m∠2 Given
BC=DC Given
AC=AC Reflexive property
△ABC≅ △ADC SAS
The triangles map onto one another with a reflection over \(\overleftrightarrow{\boldsymbol{A C}}\).
Question 5.
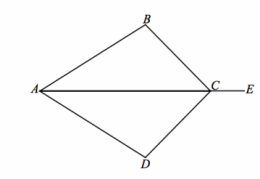
Given: \(\overline{A E}\) bisects angle ∠BCD, and BC=DC Do △CAB and △CAD meet the SAS criteria?
Answer:
\(\overline{A E}\) bisects angle ∠BCD Given
m∠BCA=m∠DCA Definition of an angle bisector
BC=DC Given
AC=AC Reflexive property
△CAD≅ △CAB SAS
The triangles map onto one another with a reflection over \(\overleftrightarrow{\boldsymbol{A C}}\).
Question 6.
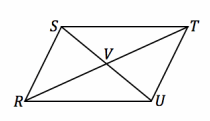
Given: \(\overline{S U}\) and \(\overline{R T}\) bisect each other Do △SVR and △UVT meet the SAS criteria?
Answer:
\(\overline{S U}\) and \(\overline{R T}\) bisect each other Given
SV=UV Definition of a segment bisector
RV=VT Definition of a segment bisector
m∠SVR=m∠UVT Vertical angles are equal in measure
△SVR≅ △UVT SAS
The triangles map onto one another with a 180° rotation about V.
Question 7.
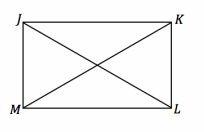
Given: JM=KL, \(\overline{J M}\) ⊥\(\overline{M L}\) , and \(\overline{K L}\) ⊥\(\overline{M L}\) Do △JML and △KLM meet the SAS criteria?
Answer:
JM=KL Given
\(\overline{J M}\) ⊥\(\overline{M L}\) , \(\overline{K M}\) ⊥\(\overline{M L}\) Given
m∠JML=90°, m∠KLM=90° Definition of perpendicular lines
m∠JML=m∠KLM Transitive property
ML=LM Reflexive property
△JML≅ △KLM SAS
The triangles map onto one another with a reflection over the perpendicular bisector of \(\overline{M L}\).
Question 8.
Given: \(\overline{B F}\) ⊥\(\overline{A C}\) , and \(\overline{C E}\) ⊥\(\overline{A B}\)
Do △BED and △CFD meet the SAS criteria?
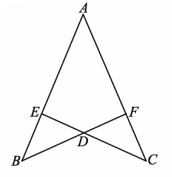
Answer:
There is not enough information given.
Question 9.
Given: m∠VXY=m∠VYX Do △VXW and △VYZ meet the SAS criteria?
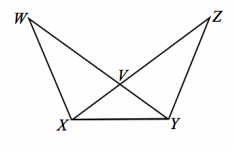
Answer:
There is not enough information given.
Question 10.
Given: △RST is isosceles, with RS=RT, and SY=TZ Do △RSY and △RTZ meet the SAS criteria?
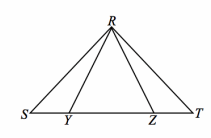
Answer:
△RST is isosceles with RS=RT Given
m∠S=m∠T Base angles of an isosceles triangle are equal in measure.
SY=TZ Given
△RSY≅ △RTZ SAS
Eureka Math Geometry Module 1 Lesson 22 Exit Ticket Answer Key
If two triangles satisfy the SAS criteria, describe the rigid motion(s) that would map one onto the other in the following cases.
Question 1.
The two triangles share a single common vertex.
Answer:
Rotation, reflection
Question 2.
The two triangles are distinct from each other.
Answer:
Translation, rotation, reflection
Question 3.
The two triangles share a common side.
Answer:
Reflection