Engage NY Eureka Math Geometry Module 1 Lesson 2 Answer Key
Eureka Math Geometry Module 1 Lesson 2 Exercise Answer Key
Opening Exercise
You need a compass, a straightedge, and another student’s Problem Set.
Directions:
Follow the directions from another student’s Problem Set write-up to construct an equilateral triangle.
→ What kinds of problems did you have as you followed your classmate’s directions?
→ Think about ways to avoid these problems. What criteria or expectations for writing steps in constructions should be included in a rubric for evaluating your writing? List at least three criteria.
Eureka Math Geometry Module 1 Lesson 2 Exploratory Challenge Answer Key
Exploratory Challenge 1.
You need a compass and a straightedge.
Using the skills you have practiced, construct three equilateral triangles, where the first and second triangles share a common side and the second and third triangles share a common side. Clearly and precisely list the steps needed to accomplish this construction.
Switch your list of steps with a partner, and complete the construction according to your partner’s steps. Revise your drawing and list of steps as needed.
Construct three equilateral triangles here:
Answer:
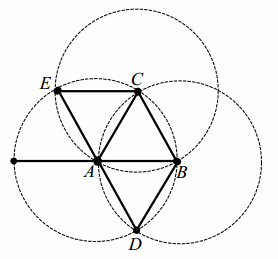
1. Draw a segment AB.
2. Draw circle A: center A, radius AB.
3. Draw circle B: center B, radius BA.
4. Label one intersection as C; label the other intersection as D.
5. Draw circle C: center C, radius CA.
6. Label the intersection of circle C with circle A (or the intersection of circle C with circle B) as E.
7. Draw all segments that are congruent to \(\overline{A B}\) between the labeled points.
There are many ways to address Step 7; students should be careful to avoid making a blanket statement that would allow segment BE or segment CD.
Exploratory Challenge 2.
On a separate piece of paper, use the skills you have developed in this lesson to construct a regular hexagon. Clearly and precisely list the steps needed to accomplish this construction. Compare your results with a partner, and revise your drawing and list of steps as needed.
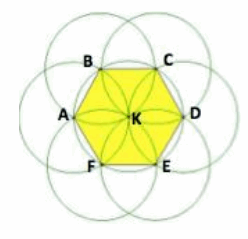
Answer:
1. Draw circle K: center K, any radius.
2. Pick a point on the circle; label this point A.
3. Draw circle A: center A, radius AK.
4. Label the intersections of circle A with circle K as B and F.
5. Draw circle B: center B, radius BK.
6. Label the intersection of circle B with circle K as C.
7. Continue to treat the intersection of each new circle with circle K as the center of a new circle until the next circle to be drawn is circle A.
8. Draw \(\overline{A B}\), \(\overline{B C}\), \(\overline{C D}\), \(\overline{D E}\), \(\overline{E F}\), \(\overline{F A}\).
Can you repeat the construction of a hexagon until the entire sheet is covered in hexagons (except the edges, which are partial hexagons)?
Answer:
Yes, this result resembles wallpaper, tile patterns, etc.
Eureka Math Geometry Module 1 Lesson 2 Problem Set Answer Key
Why are circles so important to these constructions? Write out a concise explanation of the importance of circles in creating equilateral triangles. Why did Euclid use circles to create his equilateral triangles in Proposition 1? How does construction of a circle ensure that all relevant segments are of equal length?
Answer:
The radius of equal-sized circles, which must be used in construction of an equilateral triangle, does not change. This consistent length guarantees that all three side lengths of the triangle are equal.
Eureka Math Geometry Module 1 Lesson 2 Exit Ticket Answer Key
△ABC is shown below. Is it an equilateral triangle? Justify your response.
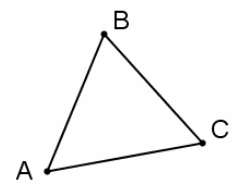
Answer:
The triangle is not equilateral. Students may prove this by constructing two intersecting circles using any two vertices as the given starting segment. The third vertex will not be one of the two intersection points of the circles.