Engage NY Eureka Math Geometry Module 1 Lesson 12 Answer Key
Eureka Math Geometry Module 1 Lesson 12 Exercise Answer Key
Opening Exercises
a. Find the measure of each lettered angle in the figure below.
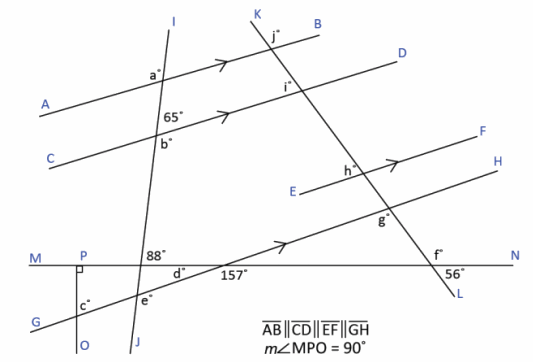
Answer:
a=115
b=115
c=67
d=23
e=115
f=124
g=101
h=79
i=79
j=101
b. Given: m∠CDE=m∠BAC
Prove: m∠DEC=m∠ABC
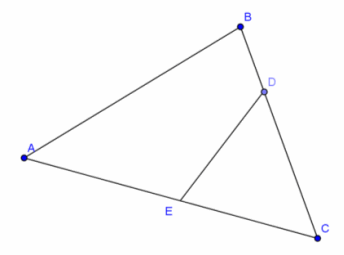
Answer:
m∠CDE=m∠BAC Given
m∠CDE+m∠DCE+m∠DEC=180° Sum of the angle measures in a triangle is 180°
m∠BAC+m∠DCE+m∠ABC=180° Sum of the angle measures of a triangle is 180°
m∠CDE+m∠DCE+m∠DEC Substitution property of equality
m∠BAC+m∠DCE+m∠ABC
m∠DEC=m∠ABC Subtraction property of equality
Mathematical Modeling Exercise
You will work with a partner on this exercise and are allowed a protractor, compass, and straightedge.
→ Partner A: Use the card your teacher gives you. Without showing the card to your partner, describe to your partner how to draw the transformation indicated on the card. When you have finished, compare your partner’s drawing with the transformed image on your card. Did you describe the motion correctly?
→ Partner B: Your partner is going to describe a transformation to be performed on the figure on your card. Follow your partner’s instructions and then compare the image of your transformation to the image on your partner’s card.
Discussion
Explaining how to transform figures without the benefit of a coordinate plane can be difficult without some important vocabulary. Let’s review.
The word transformation has a specific meaning in geometry. A transformation F of the plane is a function that assigns to each point P of the plane a unique point F(P) in the plane. Transformations that preserve lengths of segments and measures of angles are called ___. A dilation is an example of a transformation that preserves ___ measures but not the lengths of segments. In this lesson, we work only with rigid transformations.
We call a figure that is about to undergo a transformation the ___, while the figure that has undergone the transformation is called the ___.
Answer:
The word transformation has a specific meaning in geometry. A transformation F of the plane is a function that assigns to each point P of the plane a unique point F(P) in the plane. Transformations that preserve lengths of segments and measures of angles are called basic rigid motions. A dilation is an example of a transformation that preserves angle measures but not the lengths of segments. In this lesson, we work only with rigid transformations. We call a figure that is about to undergo a transformation the pre-image, while the figure that has undergone the transformation is called the image.
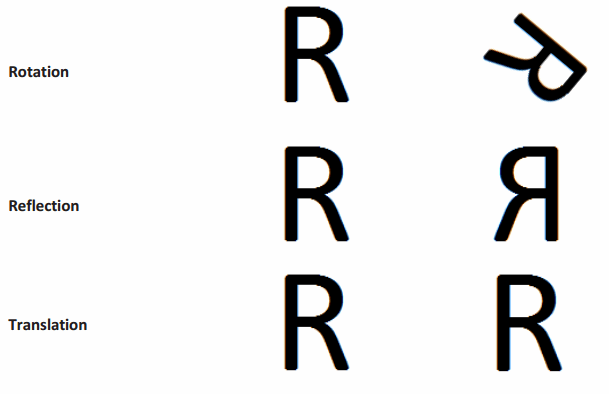
Using the figures above, identify specific information needed to perform the rigid motion shown.
For a rotation, we need to know:
Answer:
Center of rotation, direction (Clockwise (CW) or Counterclockwise (CCW)) and number of degrees rotated.
For a reflection, we need to know:
Answer:
The line of reflection acts as the perpendicular bisector of each segment that joins a given vertex of the pre-image with the respective vertex of the image.
For a translation, we need to know:
Answer:
The point P to be translated, the length and degree measure of the angle that the vector makes with the line that passes through P, and the endpoint of the vector.
Eureka Math Geometry Module 1 Lesson 12 Problem Set Answer Key
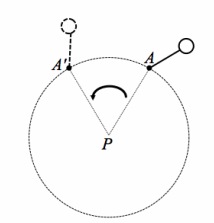
An example of a rotation applied to a figure and its image is provided. Use this representation to answer the questions that follow. For each question, a pair of figures (pre-image and image) is given as well as the center of rotation. For each question, identify and draw the following:
i. The circle that determines the rotation, using any point on the pre-image and its image.
ii. An angle, created with three points of your choice, which demonstrates the angle of rotation.
Example of a Rotation:
Pre-image: (solid line)
Image: (dotted line)
Center of rotation: P
Angle of rotation: ∠APA’
Question 1.
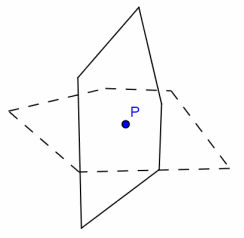
Pre-image: (solid line)
Image: (dotted line)
Center of rotation: P
Angle of rotation: _____
Answer:
90°, 270° CW
Question 2.
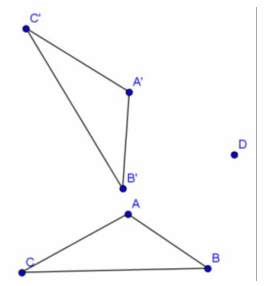
Pre-image: △ABC
Image: △A’ B’ C’
Center: D
Angle of rotation: ___
Answer:
300°, 60° CW
Eureka Math Geometry Module 1 Lesson 12 Exit Ticket Answer Key
How are transformations and functions related? Provide a specific example to support your reasoning.
Answer:
Transformations are functions. They take a set of points as inputs, apply a given rule, and output a new location for the image of the input points. Examples are a reflection across a line of reflection and a rotation of 30 degrees around a point of a given figure.