Eureka Math Geometry Module 1 Lesson 1 Answer Key

Engage NY Eureka Math Geometry Module 1 Lesson 1 Answer Key

Eureka Math Geometry Module 1 Lesson 1 Exercise Answer Key

Opening Exercise
Joe and Marty are in the park playing catch. Tony joins them, and the boys want to stand so that the distance between any two of them is the same. Where do they stand?
How do they figure this out precisely? What tool or tools could they use?

Fill in the blanks below as each term is discussed:
a. Segment The _______ between points A and B is the set consisting of A, B, and all points on the line AB between A and B.
Answer:
Segment The _______ between points A and B is the set consisting of A, B, and all points on the line AB between A and B.

b. __ A segment from the center of a circle to a point on the circle
Answer:
Radius A segment from the center of a circle to a point on the circle

c. ___ Given a point C in the plane and a number r>0, the _______ with center C and radius r is the set of all points in the plane that are distance r from point C.
Answer:
Circle Given a point C in the plane and a number r>0, the _______ with center C and radius r is the set of all points in the plane that are distance r from point C.

Note that because a circle is defined in terms of a distance, r, we often use a distance when naming the radius (e.g., “radius AB”). However, we may also refer to the specific segment, as in “radius \(\overline{A B}\)”.

Eureka Math Geometry Module 1 Lesson 1 Example Answer Key

Example 1.
Sitting Cats
You need a compass and a straightedge.
Margie has three cats. She has heard that cats in a room position themselves at equal distances from one another and wants to test that theory. Margie notices that Simon, her tabby cat, is in the center of her bed (at S), while JoJo, her Siamese, is lying on her desk chair (at J). If the theory is true, where will she find Mack, her calico cat? Use the scale drawing of Margie’s room shown below, together with (only) a compass and straightedge. Place an M where Mack will be if the theory is true.

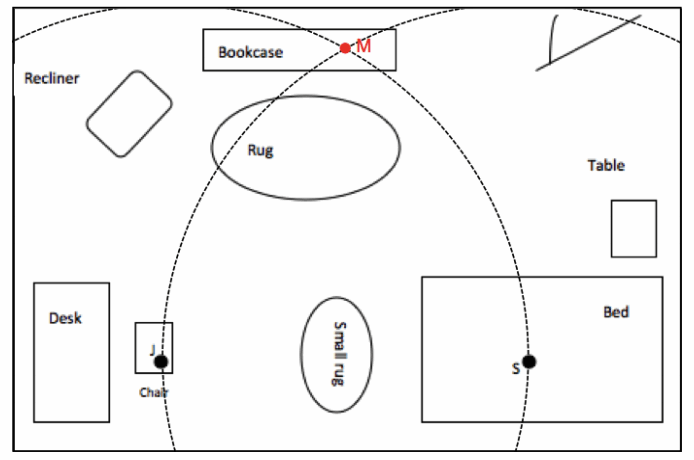
Mathematical Modeling Exercise: Euclid, Proposition 1
Let’s see how Euclid approached this problem. Look at his first proposition, and compare his steps with yours.

Proposition 1

In this margin, compare your steps with Euclid’s.

To construct an equilateral triangle on a given finite straight-line.

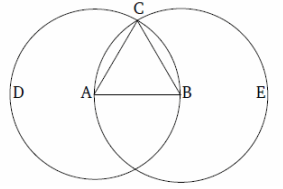
Let AB be the given finite straight-line.
So it is required to construct an equilateral triangle on the straight-line AB.

Let the circle BCD with center ,4 and radius AB have been drawn [Post. 3], and again let the circle ACE with center B and radius BA have been drawn [Post. 3]. And let the straight-lines CA and CB have been joined from the point C, where die circles cut one another, to the points A and B (respectively) [Post. 1].

And since the point A is the center of the circle CDB, AC is equal to AB [Def. 1.15]. Again, since the point B is the center of the circle CAE, BC is equal to BA [Def. 1.15]. But CA was also shown (to be) equal to AB. Thus, CA and CB are each equal to AI?. But things equal to the same thing are also equal to one another [C.N. 1]. Thus, CA is also equal to CB. Thus, the three (straightlines) CA, AB, and BC are equal to one another.

Thus, the triangle ABC is equilateral, and has been constructed on the given finite straight-line AB. (Which is) the very thing it was required to do.

Eureka Math Geometry Module 1 Lesson 1 Problem Set Answer Key

Question 1.
Write a clear set of steps for the construction of an equilateral triangle. Use Euclid’s Proposition 1 as a guide.
Answer:
1. Draw circle J: center J, radius JS.
2. Draw circle S: center S, radius SJ.
3. Label one intersection as M.
4. Join S, J, M.

Question 2.
Suppose two circles are constructed using the following instructions:
Draw circle: center A, radius \(\overline{A B}\).
Draw circle: center C, radius \(\overline{C D}\).

Under what conditions (in terms of distances AB, CD, AC) do the circles have
a. One point in common?
Answer:
If AB+CD=AC or AC+AB=CD or AC+CD=AB.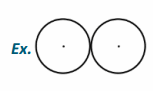

b. No points in common?
Answer:
If AB+CD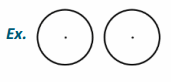

c. Two points in common?
Answer:
If AC<AB+CD and CD<AB+AC and AB<CD+AC.

d. More than two points in common? Why?
Answer:
If A=C (same points) and AB=CD. All the points of the circle coincide since the circles themselves coincide.

Question 3.
You need a compass and a straightedge.
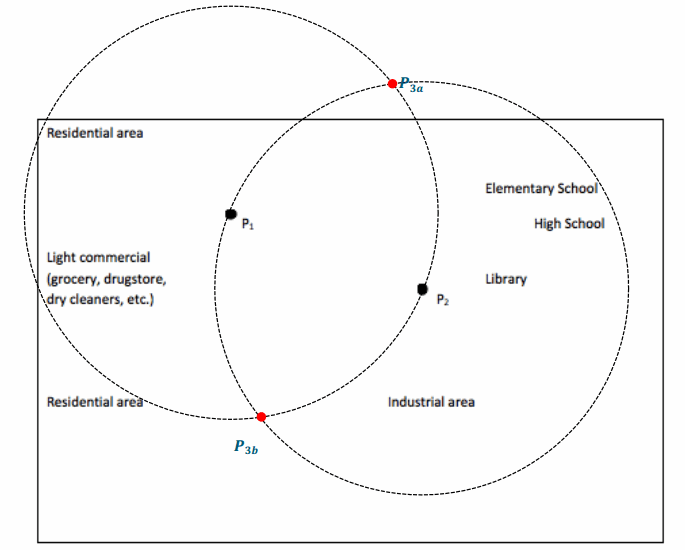
Cedar City boasts two city parks and is in the process of designing a third. The planning committee would like all three parks to be equidistant from one another to better serve the community. A sketch of the city appears below, with the centers of the existing parks labeled as P₁ and P₂. Identify two possible locations for the third park, and label them as P_3a and P_3b on the map. Clearly and precisely list the mathematical steps used to determine each of the two potential locations.
Answer:
1. Draw a circle P₁: center P₁, radius \(\overline{P_{1} P_{2}}\).
2. Draw a circle P₂: center P₂ radius \(\overline{\boldsymbol{P}_{2} \boldsymbol{P}_{1}}\).
3. Label the two intersections of the circles as P_3a and P_3b.
4. Join P₁, P₂, P_3a and P₁, P₂, P_3b.

Eureka Math Geometry Module 1 Lesson 1 Exit Ticket Answer Key

We saw two different scenarios where we used the construction of an equilateral triangle to help determine a needed location (i.e., the friends playing catch in the park and the sitting cats). Can you think of another scenario where the construction of an equilateral triangle might be useful? Articulate how you would find the needed location using an equilateral triangle.
________________________________
________________________________
Answer:
Students might describe a need to determine the locations of fire hydrants, friends meeting at a restaurant, or parking lots for a stadium, etc.