Eureka Math Algebra 2 Module 3 Lesson 4 Answer Key

Engage NY Eureka Math Algebra 2 Module 3 Lesson 4 Answer Key

Eureka Math Algebra 2 Module 3 Lesson 4 Opening Exercise Answer Key

Opening Exercise:

Write each exponential expression as a radical expression, and then use the definition and properties of radicals to write the resulting expression as an integer.

a. \(7^{\frac{1}{2}}\) . \(7^{\frac{1}{2}}\)
Answer:
√7 . √7 = √49 = 7

b. \(3^{\frac{1}{3}} \cdot 3^{\frac{1}{3}} \cdot 3^{\frac{1}{3}}\)
Answer:
\(\sqrt[3]{3}\) . \(\sqrt[3]{3}\) . \(\sqrt[3]{3}\) = \(\sqrt[3]{9}\) . \(\sqrt[3]{3}\) = \(\sqrt[3]{27}\) = 3

c. \(12^{\frac{1}{2}} \cdot 3^{\frac{1}{2}}\)
Answer:
√12 . √3 = \(\sqrt{12 \cdot 3}\) = √36 = 6

d. \(\left(64^{\frac{1}{3}}\right)^{\frac{1}{2}}\)
Answer:
\(\sqrt{\sqrt[3]{64}}\) = √64 = 8

Eureka Math Algebra 2 Module 3 Lesson 4 Example Answer Key

Examples 1 – 3:

Write each expression in the form \(b^{\frac{m}{n}}\) for positive real numbers b and integers m and n with n > 0 by applying the properties of radicals and the definition of th root.

Example 1.
\(b^{\frac{1}{4}}\) \(b^{\frac{1}{4}}\)
Answer:
By the definition of nth root,
\(b^{\frac{1}{4}}\) \(b^{\frac{1}{4}}\) = \(\sqrt[4]{b}\) . \(\sqrt[4]{b}\)
= \(\sqrt[4]{b \cdot b}\) By the properties of radicals and properties of exponents
= \(\sqrt[4]{b^{2}}\)
= \(b^{\frac{2}{4}}\) By the definition of \(b^{\frac{m}{n}}\)

The rational number \(b^{\frac{2}{4}}\) is equal to \(b^{\frac{1}{2}}\). Thus,
\(b^{\frac{1}{4}}\) . \(b^{\frac{1}{4}}\) = \(b^{\frac{1}{2}}\)

Example 2.
\(b^{\frac{1}{3}}\) . \(b^{\frac{4}{3}}\)
Answer:

Example 3.
\(b^{\frac{1}{5}}\) . \(b^{\frac{3}{4}}\)
Answer:
Write the exponents as equivalent fractions with the same denominator.
\(b^{\frac{1}{5}}\) . \(b^{\frac{3}{4}}\) = \(b^{\frac{4}{20}}\) . \(b^{\frac{15}{20}}\)

Rewrite in radicalform = \(\sqrt[20]{b^{4}} \cdot \sqrt[20]{b^{15}}\)

Rewrite as a single radical expression = \(\sqrt[20]{b^{4} \cdot b^{15}}\)
= \(\sqrt[20]{b^{19}}\)

Rewrite in exponent form using the definition = \(b^{\frac{19}{20}}\)
Thus,
\(b^{\frac{1}{5}}\) . \(b^{\frac{3}{4}}\) = \(b^{\frac{19}{20}}\)

Example 4.
Rewrite the radical expression \(\sqrt{48 x^{5} y^{4} z^{2}}\) so that no perfect square factors remain inside the radical.
Answer:

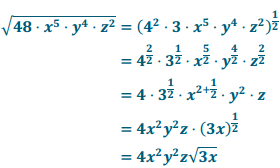
Eureka Math Algebra 2 Module 3 Lesson 4 Exercise Answer Key

Exercises 1-4:

Write each expression in form b. If a numeric expression is a rational number, then write your answer without exponents.

Exercise 1.
\(b^{\frac{2}{3}}\) . \(b^{\frac{1}{2}}\)
Answer:
\(b^{\frac{2}{3}+\frac{1}{2}}=b^{\frac{7}{6}}\)

Exercise 2.
\(\left(b^{-\frac{1}{5}}\right)^{\frac{2}{3}}\)
Answer:
\(b^{-\frac{1}{5} \cdot \frac{2}{3}}=b^{-\frac{2}{15}}\)

Exercise 3.
\(64^{\frac{1}{3}}\) . \(64^{\frac{1}{3}}\)
Answer:
\(64^{\frac{1}{3}+\frac{3}{2}}=64^{\frac{11}{6}}\)
= \((\sqrt[6]{64})^{11}\)
= 2¹¹
= 2048

Exercise 4.
\(\left(\frac{9^{3}}{4^{2}}\right)^{\frac{3}{2}}\)
Answer:
\(\left(\frac{9^{3}}{4^{2}}\right)^{\frac{3}{2}}=\frac{9^{\frac{9}{2}}}{4^{3}}\)

= \(\frac{(\sqrt[2]{9})^{9}}{64}\)

= \(\frac{3^{9}}{64}\)

= \(\frac{19683}{64}\)

Exercise 5.
Use the definition of rational exponents and properties of exponents to rewrite each expression with rational exponents containing as few fractions as possible. Then, evaluate each resulting expression for x = 50, y = 12, and z = 3.

a. \(\sqrt{8 x^{3} y^{2}}\)
Answer:
\(\sqrt{8 x^{3} y^{2}}\) = \(2^{\frac{3}{2}} x^{\frac{3}{2}} y^{\frac{2}{2}}\)
= 2xy . \((2 x)^{\frac{1}{2}}\)

Evaluating, we get 2(50) (12) (2.50)^{\(\frac{1}{2}\)} = 100 . 12 . 10 = 12000.

b. \(\sqrt[3]{54 y^{7} z^{2}}\)
Answer:
\(\sqrt[3]{54 y^{7} z^{2}}\) = \(27^{\frac{1}{3}}\) . \(2^{\frac{1}{3}}\) . \(y^{\frac{1}{3}}\) . \(z^{\frac{1}{3}\)
= 3y² . (2yz²)^{\(\frac{1}{3}\)}
Evaluating, we get 3(12)² (2 . 12 . 3²)^{\(\frac{1}{3}\)}
= 3(144)(216)^{\(\frac{1}{3}\)} = 3 . 144 . 6 = 2592

Exercise 6.
Order these numbers from smallest to largest. Explain your reasoning.
16^2.5  9^3.6  32^1.2
Answer:
The number 16^2.5 is between 256 and 4,096. We can rewrite 16^2.5 = (2⁴)^2.5, which is 2¹⁰, so 16^2.5 = 2¹⁰ = 1024.

The number 32^1.2 is between 32 and 1,024. We can rewrite 32^1.2 = (2⁵)^1.2, which is 2⁶, so 32^1.2 = 2⁶ = 64.

The number 9^3.6 is larger than 9³, so 9^3.6 is larger than 729.

Thus, 32^1.2 is clearly the smallest number, but we need to determine if 9^3.6 is greater than or less than 1,024. To do this, we know that 9^3.6 = 9^{3 + 0.6} = 9³ . 9^0.6 This means that 9^3.6 > 9³ 9^0.5, and 9³ . 9^0.5 = 729.3, which is greater than 1,024.

Thus, the numbers in order from smallest to largest are 32^1.2, 16^2.5, and 9^3.6

Eureka Math Algebra 2 Module 3 Lesson 4 Problem Set Answer Key

Question 1.
Evaluate each expression for a = 27 and b = 64.

a. \(\sqrt[3]{a} \sqrt{b}\)
Answer:
\(\sqrt[3]{27}\) . √64 = 3 . 8 = 24

b. \((3 \sqrt[3]{a} \sqrt{b})^{2}\)
Answer:
(3 . 3 . 8)² = 5184

c. \((\sqrt[3]{a}+2 \sqrt{b})^{2}\)
Answer:
(3 + 2.8)² = 361

d. \(a^{-\frac{2}{3}}+b^{\frac{3}{2}}\)
Answer:
\(\frac{1}{(\sqrt[3]{27})^{2}}\) + \((\sqrt{64})^{3}\)
= \(\frac{1}{9}\) + 512 = \(512 \frac{1}{9}\)

e. \(\left(a^{-\frac{2}{3}} \cdot b^{\frac{3}{2}}\right)^{-1}\)
Answer:
(\(\frac{1}{9}\) . 512)^-1 = \(\frac{9}{512}\)

f. \(\left(a^{-\frac{2}{3}}-\frac{1}{8} b^{\frac{3}{2}}\right)^{-1}\)
Answer:
\(\left(\frac{1}{9}-\frac{1}{8} \cdot 512\right)^{-1}\) = \(\left(-\frac{575}{9}\right)^{-1}\)
= –\(\frac{9}{575}\)

Question 2.
Rewrite each expression so that each term is in the form kxⁿ, where k is a real number, x is a positive real number, and n is a rational number.

a. \(x^{-\frac{2}{3}} \cdot x^{\frac{1}{3}}\)
Answer:
x^{\(-\frac{1}{3}\)}

b. 2x^{\(\frac{1}{2}\)} . 4x^{\(-\frac{5}{2}\)}
Answer:
8x^-2

c. \(\frac{10 x^{\frac{1}{3}}}{2 x^{2}}\)
Answer:
\(5 x^{-\frac{5}{3}}\)

d. \(\left(3 x^{\frac{1}{4}}\right)^{-2}\)
Answer:
\(\frac{1}{9} x^{-\frac{1}{2}}\)

e. \(\mathbf{x}^{\frac{1}{2}}\) (2x² – \(\frac{4}{x}\))
Answer:
2x^{\(\frac{5}{2}\)} – 4x^{\(\frac{1}{2}\)}

f. \(\sqrt[3]{\frac{27}{x^{6}}}\)
Answer:
3x^-2

g. \(\sqrt[3]{x}\) . \(\sqrt[3]{-8 x^{2}}\) . \(\sqrt[3]{27 x^{4}}\)
Answer:
-6x^{\(\frac{7}{3}\)}

h. \(\frac{2 x^{4}-x^{2}-3 x}{\sqrt{x}}\)
Answer:
2x^{\(\frac{7}{2}\)} – x^{\(\frac{3}{2}\)} – 3x^{\(\frac{1}{2}\)}

i. \(\frac{\sqrt{x}-2 x^{-3}}{4 x^{2}}\)
Answer:
\(\frac{1}{4} x^{-\frac{3}{2}}\) – \(\frac{1}{2} x^{-5}\)

Question 3.
Show that (√x + √y)² is not equal to x¹ + y¹ when x = 9 and y = 16.
Answer:
When x = 9 and y = 16, the two expressions are (√9 + √16)² and 9 + 16. The first expression simplifies to 49, and the second simplifies to 25. The two expressions are not equal.

Question 4.
Show that (x^{\(\frac{1}{2}\)} + y^{\(\frac{1}{2}\)})^-1 is not equal to \(\frac{1}{x^{\frac{1}{2}}}+\frac{1}{y^{\frac{1}{2}}}\) when x = 9 and y = 16.
Answer:
When x = 9 and y= 16, the two expressions are (√9 + √16)^-1 and \(\frac{1}{\sqrt{9}}+\frac{1}{\sqrt{16}}\). The first expression is \(\frac{1}{7^{\prime}}\) and the second one is \(\frac{1}{3}+\frac{1}{4}=\frac{7}{12}\). The two expressions are not equal.

Question 5.
From these numbers, select (a) one that is negative, (b) one that is irrational, (c) one that is not a real number, and (d) one that is a perfect square:

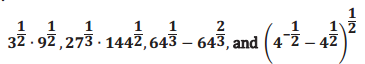
Answer:
the first number, 3^{\(\frac{1}{2}\)} . 9^{\(\frac{1}{2}\)}, is irrational;
the second number, 27^{\(\frac{1}{3}\)} . 144^{\(\frac{1}{2}\)}, is a perfect square; the third number , 64^{\(\frac{1}{3}\)} – 64^{\(\frac{2}{3}\)}, is a negative; and the last number, (4^{–\(\frac{1}{2}\)} – 4^{\(\frac{1}{2}\)})^{\(\frac{1}{2}\)}, is not a real number.

Question 6.
Show that for any rational number n, the expression 2ⁿ 4^{n + 1} . (\(\frac{1}{8}\))ⁿ equal to 4.
Answer:8
2ⁿ . 2^{2n + 2} . 2^-3n = 2² = 4

Question 7.
Let n be any rational number. Express each answer as a power of 10.

a. Multiply 10ⁿ by 10.
Answer:
10ⁿ . 10 = 10^{n + 1}

b. Multiply √10 by 10ⁿ.
Answer:
10^{\(\frac{1}{2}\)} . 10ⁿ = 10^{\(\frac{1}{2}\) + n}

c. Square 10ⁿ
Answer:
(10ⁿ)² = 10²ⁿ

d. Divide 100 . 10ⁿ by 10²ⁿ.
Answer:
\(\frac{100 \cdot 10^{n}}{10^{2 n}}\) = 10^{2 + n – 2n} = 10^{2 – n}

e. Show that 10ⁿ = 11 . 10ⁿ – 10^{n + 1}
Answer:
11 . 10ⁿ – 10^{n + 1} = 11 . 10ⁿ – 10ⁿ . 10ⁿ
= 10ⁿ(11 – 10)
= 10ⁿ . 1
= 10ⁿ

Question 8.
Rewrite each of the following radical expressions as an equivalent exponential expression in which each variable occurs no more than once.

a. \(\sqrt{8 x^{2} y}\)
Answer:
\(\sqrt{8 x^{2} y}\) = \(2^{\frac{2}{2}} x^{\frac{2}{2}}(2 y)^{\frac{1}{2}}\)
= 2x . (2y)^{\(\frac{1}{2}\)}
= 2^{\(\frac{3z}{2}\)} x y^{\(\frac{1}{2}\)}

b. \(\sqrt[5]{96 x^{3} y^{15} z^{6}}\)
Answer:
\(\sqrt[5]{96 x^{3} y^{15} z^{6}}\) = (32 . 3 . x³ . y¹⁵ .z⁶)^{\(\frac{1}{5}\)}

= \(32^{\frac{1}{5}} \cdot 3^{\frac{1}{5}} \cdot x^{\frac{3}{5}} \cdot y^{\frac{15}{5}} \cdot z^{\frac{6}{5}}\)

= 2 . \(3^{\frac{1}{5}} \cdot x^{\frac{3}{5}} \cdot y^{3} \cdot z^{\frac{6}{5}}\)

Question 9.
Use properties of exponents to find two integers that are upper and lower estimates of the value of 4^1.6.
Answer:
4^1.5 < 4^1.6 < 4²
4^1.5 = 2³ = 8 and 4² = 16, so 8 < 4^1.6 < 16.

Question 10.
Use properties of exponents to find two integers that are upper and lower estimates of the value of 8^2.3.
Answer:
8² < 8^2.3 < 8^{2 + \(\frac{1}{3}\)}
8² = 64 and 8^{\(\frac{1}{3}\)} = 2, so 8^{2 + \(\frac{1}{3}\)} = 8² . 8^{\(\frac{1}{3}\)} = 128. Thus, 64 < 8^2.3 < 128.

Question 11.
Kepler’s third law of planetary motion relates the average distance, a, of a planet from the sun to the time, t, it takes the planet to complete one full orbit around the sun according to the equation t² = a³. When the time, t, is measured in Earth years, the distance, a, is measured in astronomical units (AU5). (One AU is equal to the average distance from Earth to the sun.)

a. Find an equation for t in terms of a and an equation for a in terms of t.
Answer:
t² = a³
t = a^{\(\frac{3}{2}\)}
a = t^{\(\frac{2}{3}\)}

b. Venus takes about 0. 616 Earth year to orbit the sun. What is its average distance from the sun?
Answer:
Because a = (0.616)^{\(\frac{2}{3}\)} ≈ 0.724, the average distance from Venus to the sun is 0.724 AU.

c. Mercury is an average distance of 0.387 AU from the sun. About how long is its orbit in Earth years?
Answer:
Because t = (0.387)^{\(\frac{2}{3}\)} ≈ 0.241, the length of Mercury’s orbit is approximately 0.241 Earth years.

Eureka Math Algebra 2 Module 3 Lesson 4 Exit Ticket Answer Key

Question 1.
Find the exact value of \(9^{\frac{11}{10}} \cdot 9^{\frac{2}{5}}\) without using a calculator.
Answer:
\(9^{\frac{11}{10}} \cdot 9^{\frac{2}{5}}\) = \(9^{\frac{11}{10}+\frac{2}{5}}\)
= 9^{\(\frac{15}{10}\)}
= 9^{\(\frac{3}{2}\)}
= \((\sqrt[2]{9})^{3}\) = 27

Question 2.
Justify that \(\sqrt[3]{8} \cdot \sqrt[3]{8}\) = √16 using the properties of exponents in at least two different ways.
Answer:
\(\sqrt[3]{8} \cdot \sqrt[3]{8}\) = 8^{\(\frac{2}{3}\)}

= \(\left(2^{3}\right)^{\frac{2}{3}}\) = 2²

= \(2^{\frac{4}{2}}\)
= \(\left(2^{4}\right)^{\frac{1}{2}}\)
= √16

16^{\(\frac{1}{2}\)} = (4 . 4)^{\(\frac{1}{2}\)}
= 4^{\(\frac{2}{3}\)} . 4^{\(\frac{2}{3}\)}
= 2 .2
= 8^{\(\frac{1}{3}\)} . 8^{\(\frac{1}{3}\)}
= \(\sqrt[3]{8} \cdot \sqrt[3]{8}\)