Engage NY Eureka Math Algebra 2 Module 3 Lesson 30 Answer Key
Eureka Math Algebra 2 Module 3 Lesson 30 Opening Exercise Answer Key
Opening Exercise:
Write a sum to represent the future amount of a structured savings plan (i.e., annuity) if you deposit $250 into an account each month for 5 years that pays 3.6% interest per year, compounded monthly. Find the future amount of your plan at the end of 5 years.
Answer:
250(1.003)59 + 250(1.003)58 + ….. + 250(1.003) + 250 = 250\(\left(\frac{(1.003)^{60}-1}{0.003}\right)\) ≈ 16407.90
The amount in the account after 5 years will be $16,407.90.
Eureka Math Algebra 2 Module 3 Lesson 30 Example Answer Key
Example:
Jack wanted to buy a $9,000 2-door sports coupe but could not pay the full price of the car all at once. He asked the car dealer if she could give him a loan where he paid a monthly payment. She told him she could give him a loan for the price of the car at an annual interest rate of 3.6% compounded monthly for 60 months (5 years).
The problems below exhibit how Jack’s car dealer used the information above to figure out how much his monthly payment of R dollars per month should be.
a. First, the car dealer imagined how much she would have in an account if she deposited $9,000 into the account and left it there for 60 months at an annual interest rate of 3.6% compounded monthly. Use the compound interest formula F = P(1 + i)n to calculate how much she would have in that account after 5 years. This is the amount she would have in the account after 5 years if Jack gave her $9, 000 for the car, and she immediately deposited it.
Answer:
F = 9000(1 + 0.003)60 = 9000(1.003)60 10772.05. Atthe end of 60 months, she would have $10,772.05 in the account.
b. Next, she figured out how much would be in an account after 5 years if she took each of Jack’s payments of R
dollars and deposited it into a bank that earned 3.6% per year (compounded monthly). Write a sum to represent the future amount of money that would be in the annuity after 5 years in terms of R, and use the sum of a geometric series formula to rewrite that sum as an algebraic expression.
Answer:
This is like the structured savings plan in Lesson 29. The future amount of money in the account after 5 years can be represented as
R(1.003) + R(1.003)58 + + R(1.003) + R.
Applying the sum of a geometric series formula
Sn = a\(\left(\frac{1-r^{n}}{1-r}\right)\)
to the geometric series above using a = R, r = 1.003, and n = 60, one gets
Sn = R\(\left(\frac{1-(1.003)^{60}}{1-1.003}\right)\) = R\(\left(\frac{(1.003)^{60}-1}{0.003}\right)\)
c. The car dealer then reasoned that, to be fair to her and Jack, the two final amounts in both accounts should be the same—that is, she should have the same amount in each account at the end of 60 months either way. Write an equation in the variable R that represents this equality.
Answer:
9000(1.003)60 = R\(\left(\frac{(1.003)^{60}-1}{0.003}\right)\)
d. She then solved her equation to get the amount R that Jack would have to pay monthly. Solve the equation in part (c) to find out how much Jack needed to pay each month.
Answer:
Solving for R in the equation above, we get
R = 9000 . (1.003)60\(\left(\frac{0.003}{(1.003)^{60}-1}\right)\) ≈ 164. 13.
Thus, Jack will need to make regular payments of $164.13 a month for 60 months.
Eureka Math Algebra 2 Module 3 Lesson 30 Exercise Answer Key
Exercise:
A college student wants to buy a car and can afford to pay $200 per month. If she plans to take out a loan at 6% interest per year with a recurring payment of $200 per month for four years, what price car can she buy?
Answer:
Ap = 200\(\left(\frac{1-(1.005)^{-48}}{0.005}\right)\) ≈ 8516.06
She can afford to take out a $8,516.06 loan. If she has no money for a down payment, she can afford a car that is about $8,500.
Mathematical Modeling Exercise:
In the Problem Set of Lesson 29, you researched the price of a car that you might like to own. In this exercise, we determine how much a car payment would be for that price for different loan options.
If you did not find a suitable car, select a car and selling price from the list below:
| Car | Selling Price |
| 2005 Pickup Truck | $9,000 |
| 2007 Two-door Small Coupe | $7,500 |
| 2003 Two-door Luxury Coupe | $10,000 |
| 2006 Small SUV | $8,000 |
| 2008 Four-Door Sedan | $8,500 |
a. When you buy a car, you must pay sales tax and licensing, and other fees. Assume that sales tax is 6% of the selling price and estimated license/title/fees are 2% of the selling price. If you put a $1, 000 down payment on your car, how much money do you need to borrow to pay for the car and taxes and other fees?
Answer:
Answers will vary. For the 2007 two-door small coupe:
7500 + 7500(0.06) + 7500(0.02) – 1000 = 7100. You would have to borrow $7,100.
b. Using the loan amount you computed above, calculate the monthly payment for the different loan options shown below:
| Loan 1 | 36-month loan at 2% |
| Loan 2 | 48-month loan at 3% |
| Loan 3 | 60-month loan at 5% |
Answer:
Answers will vary. For the 2007 two-door small coupe:
Loan 1: 7100 = R\(\left(\frac{1-\left(1+\frac{0.02}{12}\right)^{-36}}{\frac{0.02}{12}}\right)\) ; therefore, R ≈ 203.36. The monthly payment would be $203.36.
Loan 2: 7100=R\(\left(\frac{1-\left(1+\frac{0.03}{12}\right)^{-48}}{\frac{0.03}{12}}\right)\);therefore, R ≈ 157.15. The monthly payment would be $157.15.
Loan 3: 7100= R\(\left(\frac{1-\left(1+\frac{0.05}{12}\right)^{-60}}{\frac{0.05}{12}}\right)\) ;therefore, R ≈ 133.99. The monthly payment would be $133.99.
c. Which plan, if any, keeps the monthly payment under $175? Of the plans under $175 per month, why might you choose a plan with fewer months even though it costs more per month?
Answer:
Answers will vary. Loan 2 and Loan 3 are both under $175 a month. When the monthly payments are close (like Loan 2 and Loan 3), the fewer payments you make with Loan 2 means you pay less overall for that loan.
Eureka Math Algebra 2 Module 3 Lesson 30 Problem Set Answer Key
Question 1.
Benji is 24 years old and plans to drive his new car about 200 miles per week. He has qualified for first-time buyer
financing, which is a 60-month loan with 0% down at an interest rate of 4%. Use the information below to estimate the monthly cost of each vehicle.
CAR A: 2010 Pickup Truck for $12,000, 22 miles per gallon
CAR B: 2006 Luxury Coupe for $11,000, 25 miles per gallon
Gasoline: $4.00 per gallon New vehicle fees: $80 Sales Tax: 4.25%
Maintenance Costs:
(2010 model year or newer): 10% of purchase price annually
(2009 model year or older): 20% of purchase price annually
Insurance:

a. How much money will Benji have to borrow to purchase each car?
Answer:
Benji would have to borrow $12,000 for the truck and $11,000 for the coupe.
b. What is the monthly payment for each car?
Answer:
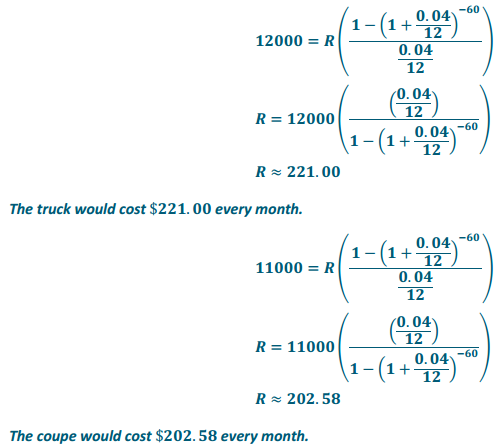
c. What are the annual maintenance costs and insurance costs for each car?
Answer:
Truck: 10% . 12000 = 1200 for the maintenance. Insurance will vary based on the gender of student. Male students will be $200 per month or $2,400 per year, while female students will be $160 per month or $1,920 per year.
Car: 20% . 11000 = 2200 for maintenance. Male students will cost $250 per month or $3,000 per year, while female students will cost $210 per month or $2,520 per year.
d. Which car should Benji purchase? Explain your choice.
Answer:
Answers will vary depending on personaipreference and experience, as well as financial backgrounds. Answers should be supported using the mathematics of parts (a), (b), and (c).
Question 2.
Use the total initial cost of buying your car from the lesson to calculate the monthly payment for the following loan options.
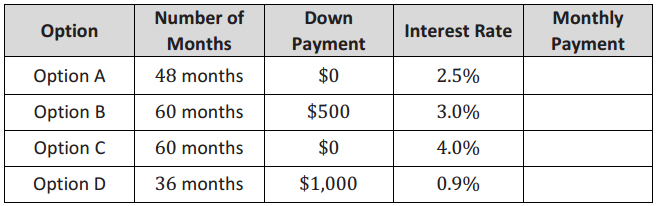
Answer:
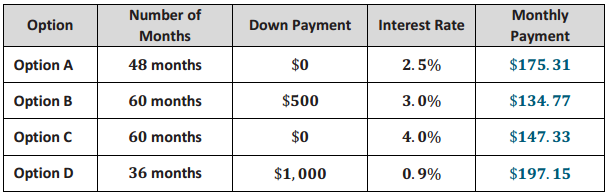
Answers will vary. Suggested answers assume an $8,000 car.
a. For each option, what is the total amount of money you will pay for your vehicle over the life of the loan?
Answer:
OptionA: $175. 31 . 48 = $8414.88
Option B: $500 + $134. 77 . 60 = $8586.20
Option C: $147. 33 . 60 = $8839.80
Option D: $1000 + $197. 15 . 36 = $8097.40
b. Which option would you choose? Justify your reasoning.
Answer:
Answers will vary. Option B is the cheapest per month but requires a down payment. Of the plans without down payments, Option A saves the most money in the end, but Option C is cheaper per month. Option D saves the most money long term but requires the largest down payment and the largest monthly payment.
Question 3.
Many lending institutions allow you to pay additional money toward the principal of your loan every month. The table below shows the monthly payment for an $8, 000 loan using Option A above if you pay an additional $25 per month.
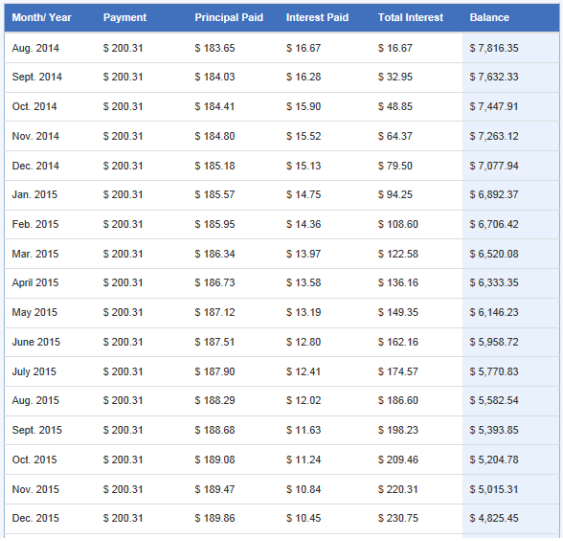
Note: The months from January 2016 to December 2016 are not shown.
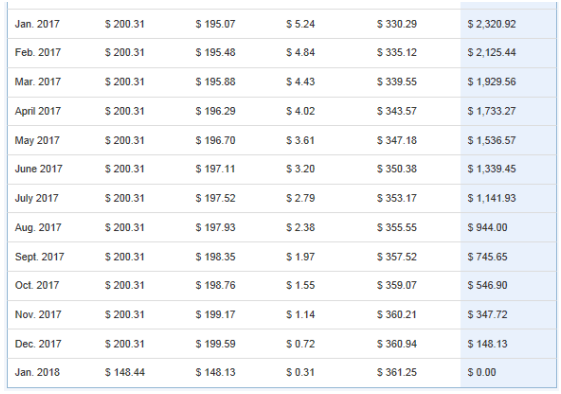
How much money would you save over the life of an $8,000 loan using Option A if you paid an extra $25 per month compared to the same loan without the extra payment toward the principal?
Answer:
Using Option A without paying extra toward the principal each month is a monthly payment of $175.31. The total amount you will pay is $8, 414.88. If you pay the extra $25 per month, you make 41 payments of $200.31 and a final payment of $148.44 for a total amount of $8,361.15. You would save $53.73.
Question 4.
Suppose you can afford only $200 a month in car payments, and your best loan option is a 60-month loan at 3%. How much money could you spend on a car? That is, calculate the present value of the loan with these conditions.
Answer:
P = 200\(\left(\frac{1-\left(1+\frac{0.03}{12}\right)^{-60}}{\frac{0.03}{12}}\right)\)
P ≈ 11130.47
You can afford a loan of about $11, 000. If there is no down payment, then the car would need to cost about $11,000.
Question 5.
Would it make sense for you to pay an additional amount per month toward your car loan? Use an online loan calculator to support your reasoning.
Answer:
While pre-paying on a loan can save you money for a relatively short-term loan like a vehicle loan, there is usually not a significant cost savings. Most students will probably elect to pocket the extra monthly costs and pay slightly more over the life of the loan. One option is paying off a loan early. That can save you more money and can be explored online as an extension question for advanced learners.
Question 6.
What is the sum of each series?
a. 900 + 900(1.01)1 + 900(1.01)2 + …. + 900(1.01)59
Answer:
900\(\left(\frac{1-(1.01)^{60}}{1-1.01}\right)\) ≈ 73502.703
b. \(\sum_{n=0}^{47}\)15000(1 + \(\frac{0.04}{12}\))n
Answer:
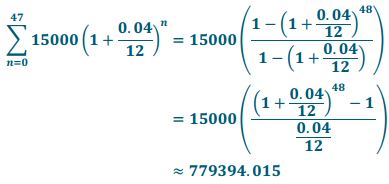
Question 7.
Gerald wants to borrow $12, 000 in order to buy an engagement ring. He wants to repay the loan by making monthly installments for two years. If the interest rate on this loan is 9 per year, compounded monthly, what is the amount of each payment?
Answer:
12000 = R\(\left(\frac{1-\left(1+\frac{0.095}{12}\right)^{-24}}{\frac{0.095}{12}}\right)\)
R = 12000\(\left(\frac{\left(\frac{0.095}{12}\right)}{1-\left(1+\frac{0.95}{12}\right)^{-24}}\right)\)
R ≈ 550.97
Gerald will need to pay $550.97 each month.
Question 8.
Ivan plans to surprise his family with a new pool using his Christmas bonus of $4,200 as a down payment. If the price of the pool is $9, 500 and Ivan can finance it at an interest rate of 2\(\frac{7}{8}\) % per year, compounded quarterly, how long is the term of the loan if his payments are $285.45 per quarter?
Answer:
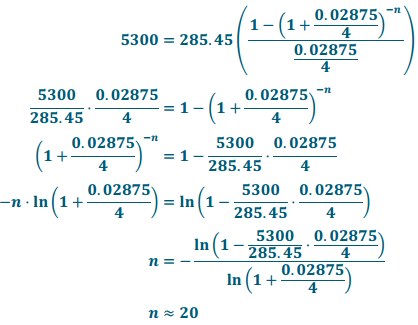 It will take Ivan 20 quarters, or five years, to pay off the pool at this rate.
It will take Ivan 20 quarters, or five years, to pay off the pool at this rate.
Question 9.
Jenny wants to buy a car by making payments of $120 per month for three years. The dealer tells her that she needs to put a down payment of $3,000 on the car in order to get a loan with those terms at a 9% interest rate per year, compounded monthly. How much is the car that Jenny wants to buy?
Answer:
P – 3000 = 120\(\left(\frac{1-\left(1+\frac{0.09}{12}\right)^{-36}}{\frac{0.09}{12}}\right)\)
P ≈ 3773.62 + 3000
The car Jenny wants to buy is about $6,773.62.
Question 10.
Kelsey wants to refinish the floors in her house and estimates that it will cost $39,000 to do so. She plans to finance the entire amount at 3% interest per year, compounded monthly for 10 years. How much is her monthly
payment?
Answer:
39000 = R\(\left(\frac{1-\left(1+\frac{0.0325}{12}\right)^{-120}}{\frac{0.0325}{12}}\right)\)
R = \(\left(\frac{\left(\frac{0.0325}{12}\right)}{1-\left(1+\frac{0.0325}{12}\right)^{-120}}\right)\)
R ≈ 381.10
Kelsey will have to pay $381.10 every month.
Question 11.
Lawrence coaches little league baseball and needs to purchase all new equipment for his team. He has $489 in donations, and the team’s sponsor will take out a loan at 4% interest per year, compounded monthly for one year, paying up to $95 per month. What is the most that Lawrence can purchase using the donations and loan?
Answer:
P – 489 = 95\(\left(\frac{1-\left(1+\frac{0.045}{12}\right)^{-12}}{\frac{0.045}{12}}\right)\)
P ≈ 489 + 1112.69
The team will have access to $1,601.69.
Eureka Math Algebra 2 Module 3 Lesson 30 Exit Ticket Answer Key
Fran wants to purchase a new boat. She starts looking for a boat around $6,000. Fran creates a budget and thinks that she can afford $250 every month for 2 years. Her bank charges her 5% interest per year, compounded monthly.
Question 1.
What is the actual monthly payment for Fran’s loan?
Answer:
6000 = R\(\left(\frac{1-\left(1+\frac{0.05}{12}\right)^{-24}}{\frac{0.05}{12}}\right)\)
R = 6000\(\left(\frac{\left(\frac{0.05}{12}\right)}{1-\left(1+\frac{0.05}{12}\right)^{-24}}\right)\)
R ≈ 263.23
The actual monthly payment for Fran’s loan would be $263.23.
Question 2.
If Fran can only pay $250 per month, what is the most expensive boat she can buy without a down payment?
Answer:
p = 250\(\left(\frac{1-\left(1+\frac{0.05}{12}\right)^{-24}}{\frac{0.05}{12}}\right)\)
P ≈ 5698.47
Fran can afford a boat that costs about $5,700 if she does not have a down payment.