Eureka Math Algebra 2 Module 3 Lesson 29 Answer Key

Engage NY Eureka Math Algebra 2 Module 3 Lesson 29 Answer Key

Eureka Math Algebra 2 Module 3 Lesson 29 Opening Exercise Answer Key

Opening Exercise:

Suppose you invested $1,000 in an account that paid an annual interest rate of 3% compounded monthly. How much would you have after 1 year?
Answer:
Since F = 1000 \(\left(1+\frac{0.03}{12}\right)^{12}\) we have F = (1.0025)¹² = $1,030.42.

Eureka Math Algebra 2 Module 3 Lesson 29 Example Answer Key

Example 1:

Let a, ar, ar², ar³, ar⁴, ….. be a geometric sequence with first term a and common ratio r. Show that the sum S_n, of the first n terms of the geometric series
S_n = a + ar + ar² + ar³ + ……. +ar^{n – 1} (r ≠ 1) is given by the equation
S_n = a\(\left(\frac{1-r^{n}}{1-r}\right)\)
Answer:
→ Multiply both sides of the equation S_n = a + ar + ar² + ar³ + ……. +ar^{n – 1} by r.
r . S_n = ar + ar² + ar³ + ……. + ar^{n – 1} + arⁿ

→ Compare the terms on the right-hand side of the old and new equations:
S_n = a + ar + ar² + ar³ + ……. +ar^{n – 1}
r . S_n = ar + ar² + ar³ + ……. + ar^{n – 1} + arⁿ

→ What are the only terms on the right-hand side of the original equation and the new equation that are not found in both?
The only terms that are not found in both are a and arⁿ.

→ Therefore, when we subtract S_n – rS_n, all the common terms on the right-hand side of the equations subtract to zero leaving only a – arⁿ (after applying the associative and commutative properties repeatedly):

S_n – rS_n = (a + ar + ar² + ….. + ar^{n – 1}) – (ar + ar² + …. + ar^{n – 1} + arⁿ)
= a + (ar – ar) + (ar² – ar²) + …. +(r^{n – 1} – ar^{n – 1}) – arⁿ
= a – arⁿ

→ Isolate S, in the equation S_n – rS_n = a – arⁿ to get the formula (when r ≠ 1):
S_n(1 – r) = a(1 – rⁿ)
⇒ S_n = a\(\left(\frac{1-r^{n}}{1-r}\right)\).

Exercises 1 – 3:

Exercise 1.
Find the sum of the geometric series 3 + 6 + 12 + 24 + 48 + 96 + 192.
Answer:
The first term is 3, so a = 3. The common ratio is 6/3 = 2, so r = 2. Since there are 7 terms, n = 7.
Thus, S₇ = 3 . \(\frac{1-2^{7}}{1-2}\), or S₇ = 381.

Exercise 2.
Find the sum of the geometric series 40 + 40(1.005) + 40(1.005)² + ……….. + 40(1.005)¹¹.
Answer:
Reading directly off the sum, a = 40, r = 1.005, and n = 12.
Thus, S₁₂ = 40 . \(\left(\frac{1-1.005^{12}}{1-1.005}\right)\), so S₁₂ ≈ 493.42.

Exercise 3.
Describe a situation that might lead to calculating the sum of the geometric series in Exercise 2.
Answer:
Investing $40 a month into an account with an annual interest rate of 6% compounded monthly (or investing $40 a month into an account with an interest rate of 0.05% per month) can lead to the geometric series in Exercise 2.

Example 2:

A $100 deposit is made at the end of every month for 12 months in an account that earns interest at an annual interest rate of 3% compounded monthly. How much will be in the account immediately after the last payment?
Answer:
The total amount is the sum 100 + 100(1.025)+ 100(1.025)² + ….. + 100(1.025)¹¹. This is a geometric series with a = 100, r = 1. 025, and n = 12. Using the formula for the sum of a geometric series, S₁₂ = 100 \(\left(\frac{1-1.025^{12}}{1-1.025}\right)\), so S ≈ 1379.56. The account will have $1, 379.56 in it immediately after the last payment.

Discussion:

An annuity is a series of payments made at fixed intervals of time. Examples of annuities include structured savings plans, lease payments, loans, and monthly home mortgage payments. The term annuity sounds like it is only a yearly payment, but annuities often require payments monthly, quarterly, or semiannually. The future amount of the annuity, denoted A_f, is the sum of all the individual payments made plus all the interest generated from those payments over the specified period of time.

We can generalize the structured savings plan example above to get a generic formula for calculating the future value of an annuity A_f, in terms of the recurring payment R, interest rate i, and number of payment periods n. In the example above, we had a recurring payment of R = 100, an interest rate per time period of i = 0.025, and 12 payments, so n = 12. To make things simpler, we always assume that the payments and the time period in which interest is compounded are at the same time. That is, we do not consider plans where deposits are made halfway through the month with interest compounded at the end of the month.

In the example, the amount A_f, of the structured savings plan annuity was the sum of all payments plus the interest accrued for each payment:

A_f = R + R(1 + i)¹ + R(1 + i)² + …. + R(1 + i)^{n – 1}

This, of course, is a geometric series with n terms, a = R, and r = 1 + i, which after substituting into the formula for a geometric series and rearranging is,
A_f = R\(\left(\frac{(1+i)^{n}-1}{i}\right)\)

Exercises 4 – 5:

Exercise 4.
Write the sum without using summation notation, and find the sum.

a. \(\sum_{k=0}^{5}\)k
Answer:
\(\sum_{k=0}^{5}\)k = 0 + 1 + 2 + 3 + 4 + 5 = 15

b. \(\sum_{k=0}^{5}\)j²
Answer:
\(\sum_{k=0}^{5}\)j² = 5² + 6² + 7² = 25 + 36 + 49 = 110

c. \(\sum_{i=2}^{4} \frac{1}{i}\)
Answer:
\(\sum_{i=2}^{4} \frac{1}{i}\) = \(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}=\frac{13}{12}\)

Exercise 5.
Write each sum using summation notation. Do not evaluate the sum.

a. 1⁴ + 2⁴ + 3⁴ + 4⁴ + 5⁴ + 6⁴ + 7⁴ + 8⁴ + 9⁴
Answer:
\(\sum_{k=1}^{9} k^{4}\)

b. 1 + cos(π) + cos(2π) + cos(3π) + cos(4π) + cos(5π)
Answer:
\(\sum_{k=0}^{5} \cos (k \pi)\)

c. 2 + 4 + 6 + …… + 1000
Answer:
\(\sum_{k=1}^{500} 2 k\)

Eureka Math Algebra 2 Module 3 Lesson 29 Problem Set Answer Key

Question 1.
A car loan is one of the first secured loans most Americans obtain. Research used car prices and specifications in your area to find a reasonable used car that you would like to own (under $10, 000). If possible, print out a picture of the car you selected.

a. What is the year, make, and model of your vehicle?
Answer:
Answers will vary. For instance, 2006 Pontiac G6 GT.

b. What is the selling price for your vehicle?
Answer:
Answers will vary. For instance, $7,500

c. The following table gives the monthly cost per $1, 000 financed on a 5-year auto loan. Assume you have qualified for a loan with a 5% annual interest rate. What is the monthly cost of financing the vehicle you selected? (A formula is developed to find the monthly payment of a loan in Lesson 30.)

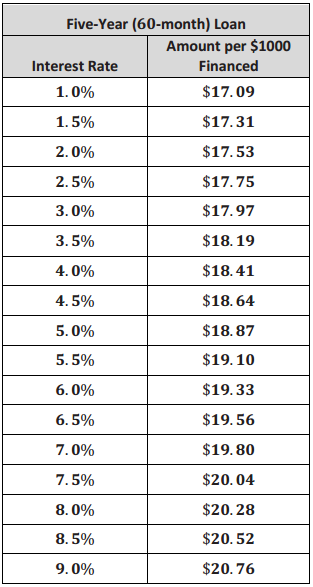
Answer:
Answers will vary. At 5% interest, financing a $7,500 car for 60 months costs $18.87 . 7 . 5, which is approximately $141.53 per month.

d. What is the gas mileage for your vehicle?
Answer:
Answers will vary. For instance, the gas mileage might be 29 miles per gallon.

e. Suppose that you drive 120 miles per week and gas costs $4 per gallon. How much does gas cost per month?
Answer:
Answers will vary but should be based on the answer to part (d). For instance, with gas mileage of 29 miles per gallon, the gas cost would be \(\frac{120}{29}\). 4.3 $4 ≈ $71.17 per month.

Question 2.
Write the sum without using summation notation, and find the sum.

a. \(\sum_{k=1}^{8} \boldsymbol{k}\)
Answer:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 4 . 9 = 36

b. \(\sum_{k=-8}^{8}\)k
Answer:
-8 + -7 + -6 + -5 + -4 + -3 + -2 + -1 + 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 0

c. \(\sum_{k=1}^{4} k^{3}\)
Answer:
1³ + 2³ + 3³ + 4³ = 1 + 8 + 27 + 64 = 100

d. \(\sum_{m=0}^{6}\)2m
Answer:
2 . 0 + 2 . 1 + 2 . 2 + 2 . 3 + 2 . 4 + 2 . 5 + 2 . 6 = 0 + 2 + 4 + 6 + 8 + 10 = 3.5 . 12 = 42

e. \(\sum_{m=0}^{6} 2 m+1\)
Answer:
(2 . 0 + 1) + (2 . 1 + 1) + (2 . 2 + 1) + (2 . 3 + 1) + (2 . 4 + 1) + (2 . 5 + 1) + (2 . 6 + 1) = 42 + 7 = 49

f. \(\sum_{k=2}^{5} \frac{1}{k}\)
Answer:
\(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}\) = \(\frac{30}{60}+\frac{20}{60}+\frac{15}{60}+\frac{12}{60}\) = \(\frac{77}{60}\)

g. \(\sum_{j=0}^{3}(-4)^{j-2}\)
Answer:

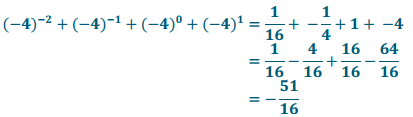
h. \(\sum_{m=1}^{4} 16\left(\frac{3}{2}\right)^{m}\)
Answer:

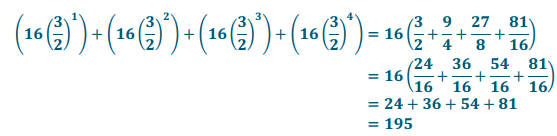
i. \(\sum_{i=0}^{3} \frac{105}{2 j+1}\)
Answer:
\(\frac{105}{2 \cdot 0+1}+\frac{105}{2 \cdot 1+1}+\frac{105}{2 \cdot 2+1}+\frac{105}{2 \cdot 3+1}\) = \(\frac{105}{1}+\frac{105}{3}+\frac{105}{5}+\frac{105}{7}\) = 105 + 35 + 21 + 15 = 176

j. \(\sum_{p=1}^{3} \boldsymbol{p} \cdot \mathbf{3}^{p}\)
Answer:
1 . 3¹ + 2 . 3² + 3 . 3³ = 3 + 18 + 54 = 102

k. \(\sum_{j=1}^{6} 100\)
Answer:
100 + 100 + 100 + 100 + 100 + 100 = 600

l. \(\sum_{k=0}^{4} \sin \left(\frac{k \pi}{2}\right)\)
Answer:
sin\(\left(\frac{0 \pi}{2}\right)\) + sin\(\left(\frac{1 \pi}{2}\right)\) + sin\(\left(\frac{2 \pi}{2}\right)\) + sin\(\left(\frac{3 \pi}{2}\right)\) + sin\(\left(\frac{4 \pi}{2}\right)\) = 0 + 1 + 0 + -1 + 0 = 0

m. \(\sum_{k=1}^{9} \log \left(\frac{k}{k+1}\right)\)
(Hint: You do not need a calculator to find the sum.)
Answer:

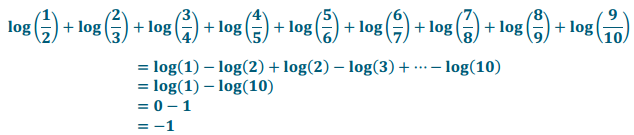
Question 3.
Write the sum without using the sigma notation.

a. \(\sum_{k=0}^{4} \sqrt{k+3}\)
Answer:

b. \(\sum_{i=0}^{8} x^{i}\)
Answer:
1 + x¹ + x² + x³ + x⁴ + x⁵ + x⁶ + x⁷ + x⁸

c. \(\sum_{j=1}^{6} j x^{j-1}\)
Answer:
1x^{1 – 1} + 2x^{2 – 1} + 3x^{3 – 1} + 4x^{4 – 1} + 5x^{5 – 1} + 6x^{6 – 1}
= 1 + 2x¹ + 3x² + 4x³ + 5x⁴ + 6x⁵

d. \(\sum_{k=0}^{9}(-1)^{k} x^{k}\)
Answer:
(-1)⁰x⁰ + (-1)¹x¹ + (-1)²x² + (-1)³x³ + (-1)⁴x⁴ + (-1)⁵x⁵+ (-1)⁶x⁶ + (-1)⁷x⁷ + (-1)⁸x⁸ + (-1)⁹x⁹
= 1 – x + x² – x³ + x⁴ – x⁵ + x⁶ – x⁷ + x⁸ – x⁹

Question 4.
Write each sum using summation notation.

a. 1 + 2 + 3 + 4 + ….. + 1000
Answer:
\(\sum_{k=1}^{1000}\)k^

b. 2 + 4 + 6 + 8 + ….. + 100
Answer:
\(\sum_{k=1}^{50}\)2k

c. 1 + 3 + 5 + 7 + ….. + 99
Answer:
\(\sum_{k=1}^{50} 2 k-1 \text { or } \sum_{k=0}^{49} 2 k+1\)

d. \(\frac{1}{2}+\frac{2}{3}+\frac{3}{4}+\cdots+\frac{99}{100}\)
Answer:
\(\sum_{k=1}^{99} \frac{k}{k+1} \text { or } \sum_{k=2}^{100} \frac{k-1}{k}\)

e. 1² + 2² + 3² + 4² + …. + 10000²
Answer:
\(\sum_{k=1}^{10000} k^{2}\)

f. 1 + x + x² + x³ + ….. + x²⁰⁰
Answer:
\(\sum_{k=0}^{200} x^{k}\)

g. \(\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\frac{1}{3 \cdot 4}+\cdots+\frac{1}{49 \cdot 50}\)
Answer:
\(\sum_{k=1}^{49} \frac{1}{k(k+1)} \text { or } \sum_{k=2}^{50} \frac{1}{(k-1) k}\)

h. 1 ln(1) + 2 ln(2) + 3 ln(3) + ….. + 10 ln(10)
Answer:
\(\sum_{k=1}^{10} k \ln (k)\)

Question 5.
Use the geometric series formula to find the sum of the geometric series.

a. 1 + 3 + 9 + …. + 2187
Answer:
\(\left(\frac{1-3^{8}}{1-3}\right)=\frac{6560}{2}\) = 3280

b. 1 + \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots+\frac{1}{512}\)
Answer:

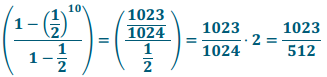
c. 1 – \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots+\frac{1}{512}\)
Answer:
\(\left(\frac{1-\left(-\frac{1}{2}\right)^{10}}{1+\frac{1}{2}}\right)=\frac{1023}{1024} \cdot \frac{2}{3}=\frac{341}{512}\)

d. 0.8 + 0.64 + 0.512 + …. + 0.32768
Answer:
0.8(\(\frac{1-0.8^{5}}{1-0.8}\)) = 0.8 . \(\frac{0.67232}{0.2}\) = 2.68928

e. 1 + √3 + 3 + 3√3 + ….. + 243
Answer:
\(\left(\frac{1-\sqrt{3}^{11}}{1-\sqrt{3}}\right)\) ≈ 573.5781477

f. \(\sum_{k=0}^{5} 2^{k}\)
Answer:
\(\left(\frac{1-2^{6}}{1-2}\right)\) = 63

g. \(\sum_{m=1}^{4} 5\left(\frac{3}{2}\right)^{m}\)
Answer:

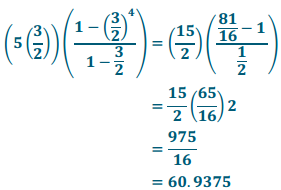
h. 1 – x + x² – x³ + …… + x³⁰ in terms of x
Answer:
\(\left(\frac{1-(-x)^{31}}{1-(-x)}\right)=\frac{x^{31}+1}{x+1}\)

i.\(\sum_{m=0}^{11} 4^{\frac{m}{3}}\)
Answer:
\(\left(\frac{1-\left(4^{\frac{1}{3}}\right)^{12}}{1-4^{\frac{1}{3}}}\right)\) ≈ 434.1156679

j. \(\sum_{n=0}^{14}(\sqrt[5]{6})^{n}\)
Answer:
\(\left(\frac{1-(\sqrt[5]{6})^{15}}{1-\sqrt[5]{6}}\right)\) ≈ 498.8756953

k. \(\sum_{k=0}^{6} 2 \cdot(\sqrt{3})^{k}\)
Answer:
2\(\left(\frac{1-\sqrt{3}^{7}}{1-\sqrt{3}}\right)\) ≈ 125.033321

Question 6.
Let a_i represent the sequence of even natural numbers {2, 4, 6, 8, … } with a₁ = 2. Evaluate the following expressions.

a. \(\sum_{i=1}^{5} a_{i}\)
Answer:
2 + 4 + 6 + 8 + 10 = 30

b. \(\sum_{i=1}^{4} a_{2 i}\)
Answer:
a₂ + a₄ + a₆ + a₈ = 4 + 8 + 12 + 16 = 40

c. \(\sum_{i=1}^{5}\left(a_{i}-1\right)\)
Answer:
(2 – 1) + (4 – 1) + (6 – 1) + (8 – 1) + (10 – 1) = 1 + 3 + 5 + 7 + 9 = 25

Question 7.
Let a_i represent the sequence of integers giving the yardage gained per rush in a high school football game (3, -2, 17, 4, -8, 19, 2, 3, 3, 4, 0, 1,-7).

a. Evaluate \(\sum_{i=1}^{13} a_{i}\). What does this sum represent in the context of the situation?
Answer:
\(\sum_{i=1}^{13} a_{i}\) = 3 + -2 + 17 + 4 + -8 + 19 + 2 + 3 + 3 + 4 + 0 + 1 + -7
= 56 + -17 = 39
This sum is the total rushing yards.

b. Evaluate \(\frac{\sum_{i=1}^{13} a_{i}}{13}\). What does this expression represent in the context of the situation?
Answer:
\(\frac{39}{13}\) = 3
The average yardage per rush is 3.

c. In general, if a_n describes any sequence of numbers, what does \(\frac{\sum_{i=1}^{n} a_{i}}{n}\) represent?
Answer:
The total divided by the number of numbers is the arithmetic mean or average of the set.

Question 8.
Let b_n represent the sequence given by the following recursive formula: b₁ = 10, b_n = 5b_{n – 1}.

a. Write the first 4 terms of this sequence.
Answer:
10, 50, 250, 1250

b. Expand the sum \(\sum_{i=1}^{4} b_{i}\). Is it easier to add this series, or is it easier to use the formula for the sum of a finite geometric sequence? Explain your answer. Evaluate \(\sum_{i=1}^{4} b_{i}\)
Answer:
\(\sum_{i=1}^{4} b_{i}\) = 10 + 50 + 250 + 1250
Answers may vary based on personal opinion. Since this series consists of only four terms, it may be easier to simply add the terms together to find the sum. The sum is 1560.

c. Write an explicit form for b_n.
Answer:
b_n = 10 . 5_{n – 1}, where n is a positive integer.

d. Evaluate \(\sum_{i=1}^{10} b_{i}\)
Answer:
(10) . \(\left(\frac{1-5^{10}}{1-5}\right)\) = 10 . \(\frac{9765624}{4}\) = 24414060

Question 9.
Consider the sequence given by a₁ = 20, a_n = \(\frac{1}{2}\) . a_{n – 1}

a. Evaluate \(\sum_{i=1}^{10} a_{i}\), \(\sum_{i=1}^{100} a_{i}\), and \(\sum_{i=1}^{1000} a_{i}\).
Answer:

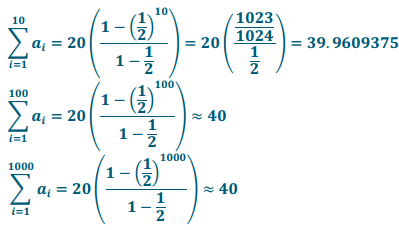
b. What value does it appear this series is approaching as n continues to increase? Why might It seem like the series is bounded?
Answer:
The series is almost exactly 40. In the numerator we are subtracting a number that is incredibly small and gets even smaller the farther we go in the sequence. So, as n → ∞, the sum approaches \(\frac{20}{\frac{1}{2}}\) = 40.

Question 10.
The sum of a geometric series with 4 terms is 60, and the common ratio is r = \(\frac{1}{2}\). Find the first term.
60 = a\(\left(\frac{1-\left(\frac{1}{2}\right)^{4}}{1-\frac{1}{2}}\right)\)
60 = a\(\left(\frac{1-\frac{1}{16}}{\frac{1}{2}}\right)\)
60 = a(\(\frac{15}{16}\) . 2)
60 = a(\(\frac{15}{8}\))
a = 4 . 8 = 32

Question 11.
The sum of the first 4 terms of a geometric series is 203, and the common ratio is 0.4. Find the first term.
Answer:
203 = \(\left(\frac{1-0.4^{4}}{1-0.4}\right)\)
a = 203\(\left(\frac{0.6}{1-0.4^{4}}\right)\) = 125

Question 12.
The third term in a geometric series is \(\frac{27}{2}\), and the common ratio is \(\frac{729}{16}\). Find the first term.
Answer:
ar² = \(\frac{27}{2}\)
ar⁵ = \(\frac{729}{16}\)
r³ = \(\frac{729}{16}\) . \(\frac{2}{27}\) = \(\frac{27}{8}\)
r = \(\frac{3}{2}\)

Question 13.
The second term in a geometric series is 10, and the seventh term is 10,240. Find the sum of the first six terms.
Answer:
ar = 10
ar⁶ = 10240
r⁵ = 1024
r = 4
a = \(\frac{10}{4}\) = \(\frac{5}{2}\)
S₆ = \(\frac{5}{2}\) \(\left(\frac{1-4^{6}}{1-4}\right)\)
= \(\frac{5}{2}\left(\frac{4095}{3}\right)\) = 3412.5

Question 14.
Find the interest earned and the future value of an annuity with monthly payments of $200 for two years into an
an account that pays 6% interest per year compounded monthly.
Answer:
A_f = 200\(\left(\frac{\left(1+\frac{0.06}{12}\right)^{24}-1}{\frac{0.06}{12}}\right)\) ≈ 5086.39
The future value is $5,086.39, and the interest earned is $286.39.

Question 15.
Find the interest earned and the future value of an annuity with annual payments of $1,200 for 15 years into an account that pays 4% interest per year.
Answer:
A_f = 1200\(\left(\frac{(1+0.04)^{15}-1}{0.04}\right)\) ≈ 24028.31
The future value is $24, 028.31, and the interest earned is $6,028.31.

Question 16.
Find the interest earned and the future value of an annuity with semiannual payments of $1,000 for 20 years into an account that pays 7% interest per year compounded semiannually.
Answer:
A_f = 100\(\left(\frac{\left(1+\frac{0.07}{2}\right)^{40}-1}{\frac{0.07}{2}}\right)\) ≈ 84550.28
The future value is $84, 550.28, and the interest earned is $44,550.28.

Question 17.
Find the interest earned and the future value of an annuity with weekly payments of $100 for three years into an account that pays 5% interest per year compounded weekly.
Answer:
A_f = 100\(\left(\frac{\left(1+\frac{0.05}{52}\right)^{156}-1}{\frac{0.05}{52}}\right)\) ≈ 16822.05
The future value is $16,822.05, and the interest earned is $1,222.05.

Question 18.
Find the interest earned and the future value of an annuity with quarterly payments of $500 for 12 years into an account that pays 3% interest per year compounded quarterly.
Answer:
A_f = 500\(\left(\frac{\left(1+\frac{0.03}{4}\right)^{48}-1}{\frac{0.03}{4}}\right)\) ≈ 28760.36
The future value is $28,760.36, and the interest earned is $4,760.36.

Question 19.
How much money should be invested every month with 8% interest per year compounded monthly in order to save up $10, 000 in 15 months?
Answer:
10000 = R\(\left(\frac{\left(1+\frac{0.08}{12}\right)^{15}-1}{\frac{0.08}{12}}\right)\)
R = 10000\(\left(\frac{\frac{0.08}{12}}{\left(1+\frac{0.08}{12}\right)^{15}-1}\right)\) ≈ 636.11
In vest $636. 11 every month for 15 months at this interest rate to save up $10,000.

Question 20.
How much money should be invested every year with 4% interest per year in order to save up $40,000 in 18 years?
Answer:
40000 = R\(\left(\frac{(1+0.04)^{18}-1}{0.04}\right)\)
R = 40000 \(\left(\frac{0.04}{(1.04)^{18}-1}\right)\) ≈ 1559.733
Invest $1,559.73 every year for 18 years at 4% interest per year to save up $40,000.

Question 21.
Julian wants to save up to buy a car. He is told that a loan for a car costs $274 a month for five years, but Julian does not need a car presently. He decides to invest in a structured savings plan for the next three years. Every month Julian invests $274 at an annual interest rate of 2% compounded monthly.

a. How much will Julian have at the end of three years?
Answer:
A_f =274\(\left(\frac{\left(1+\frac{0.02}{12}\right)^{36}-1}{\frac{0.02}{12}}\right)\) ≈ 10157.21
Julian will have $10,157.21 at the end of the three years.

b. What are the benefits of investing in a structured savings plan instead of taking a loan out? What are the drawbacks?
Answer:
The biggest benefit is that instead of paying interest on a loan, you earn interest on your savings. The drawbacks include that you have to wait to get what you want.

Question 22.
An arithmetic series is a series whose terms form an arithmetic sequence. For example, 2 + 4 + 6 + + 100 is an
arithmetic series since 2, 4, 6, 8, …, 100 is an arithmetic sequence with constant difference 2. The most famous arithmetic series is 1 + 2 + 3 + 4 + ….. + n for some positive integer n.

We studied this series in Algebra I and showed that its sum is S_n = \( = 2 . It can be shown that the general formula for the sum of an arithmetic series a + (a + d) + (a + 2d) + … + [a + (n – 1)d] is S_n = [latex]\frac{n}{2}\)[2a + (n – 1)d], where a is the first term and d is the constant difference.

a. Use the general formula to show that the sum of 1 + 2 + 3 + …. + n is S_n = \(
Answer:
S_n = [latex]\frac{n}{2}\)(2 . 1 + (n – 1) . 1) = \(\frac{n}{2}\)(2 + n – 1) = \(\frac{n}{2}\)(n + 1)

b. Use the general formula to find the sum of 2 + 4 + 6 + 8 + 10 + …. + 100.
Answer:
S_n = \(\frac{50}{2}\)(4 + (50 – 1)2) = 25(102) = 2550

Question 23.
The sum of the first five terms of an arithmetic series is 25, and the first term Is 2. Find the constant difference.
Answer:
25 = \(\frac{5}{2}\)(2 + a₅)
10 = 2 + a₅
a₅ = 8
8 = 2 + d(4)
6 = d(4)
d = \(\frac{3}{2}\)

Question 24.
The sum of the first nine terms of an arithmetic series is 135, and the first term is 17. Find the ninth term.
Answer:
135 = \(\frac{9}{2}\)(17 + a₉)
30 = 17+ a₉
13 = a₉
13 = 17 + d(8)
-4 = d(8)
d = –\(\frac{1}{2}\)

Question 25.
The sum of the first and 100th terms of an arithmetic series is 101. Find the sum of the first 100 terms.
Answer:
S₁₀₀ = \(\frac{100}{2}\)(101) = 5050.

Eureka Math Algebra 2 Module 3 Lesson 29 Exit Ticket Answer Key

Question 1.
Martin attends a financial planning conference and creates a budget for himself, realizing that he can afford to put away $200 every month in savings and that he should be able to keep this up for two years. If Martin has the choice between an account earning an interest rate of 2.3% yearly versus an account earning an annual interest rate of 2. 125% compounded monthly, which account gives Martin the largest return in two years?
Answer:
A_f = R\(\left(\frac{(1+i)^{n}-1}{i}\right)\)
A_f = 2400\(\left(\frac{(1.023)^{2}-1}{0.023}\right)\) = 4855.20
A_f = 200\(\left(\frac{\left(1+\frac{0.0215}{12}\right)^{24}-1}{\frac{0.0215}{12}}\right)\) ≈ 4900.21
The account earning an interest rate of 2.125% compounded monthly returns more than the yearly account.