Engage NY Eureka Math Algebra 2 Module 3 Lesson 28 Answer Key
Eureka Math Algebra 2 Module 3 Lesson 28 Mathematical Modeling Exercise Answer Key
Mathematical Modeling Exercise 1:
A crime scene investigator is called to the scene of a crime where a dead body has been found. He arrives at the scene and measures the temperature of the dead body at 9:30 p.m. to be 78.3°F. He checks the thermostat and determines that the temperature of the room has been kept at 74°F. At 10:30 p.m., the investigator measures the temperature of the body again.
It is now 76.8°F. He assumes that the Initial temperature of the body was 98.6°F (normal body temperature). Using this data, the crime scene investigator proceeds to calculate the time of death. According to the data he collected, what time did the person die?
a. Can we find the time of death using only the temperature measured at 9:30 p.m.? Explain.
Answer:
No. There are two parameters that are unknown, k and t. We need to know the decay constant, k, in order to be able to find the elapsed time.
b. Set up a system of two equations using the data.
Answer:
Let t1 represent the elapsed time from the time of death until 9:30 when the first measurement was taken, and let t2 represent the elapsed time between the time of death and 10:30 when the second measurement was taken. Then t2 = t1 + 1. We have the following equations:
T(t1) = 74 + (98.6 – 74)e-kt1
T(t2) = 74 + (98.6 – 74)e-kt2
Substituting in our known value T(t1) = 78.3 and T(t2) = 76.8, we get the system:
78.3 = 74+ (98.6 – 74)e-kt1
76.8 = 74+ (98.6 – 74)e-k(t1 + 1)
c. Find the value of the decay constant, k.
Answer:
4.3 = 24e-kt1
2.8 = 24.6e-k(t1 + 1)
\(\frac{4.3}{2.8}\) = e-kt1 + k(t1 + 1)
\(\frac{4.3}{2.8}\) = ek
ln(\(\frac{4.3}{2.8}\)) = ln(ek
ln(\(\frac{4.3}{2.8}\)) = k
k ≈ 0.429
d. What was the time of death?
Answer:
4.3 = 24.6e-0.429t1
\(\frac{4.3}{24.6}\) = e-0.429t1
ln(\(\frac{4.3}{24.6}\)) = ln(e-0.429t1)
ln(\(\frac{4.3}{24.6}\)) = -0.429t1
4.0656 = t1
The person died approximately 4 hours before 9:30 p.m., so the time of death was approximately 5:30 p.m.
Mathematical Modeling Exercise 2:
A pot of tea is heated to 90°C. A cup of the tea is poured into a mug and taken outside where the temperature is 18°C. After 2 minutes, the temperature of the cup of tea is approximately 65°C.
a. Determine the value of the decay constant, k.
Answer:
T(2) = 18 + (90 – 18)ek.2 = 65
72e-2k = 47
e-2k = \(\frac{47}{72}\)
-2k = ln(\(\frac{47}{72}\))
k ≈ 0.2133
b. Write a function for the temperature of the tea in the mug, T, in °C, as a function of time, t, in minutes.
Answer:
T(t) = 18 + 72 e-0.213t
c. Graph the function T.
Answer:
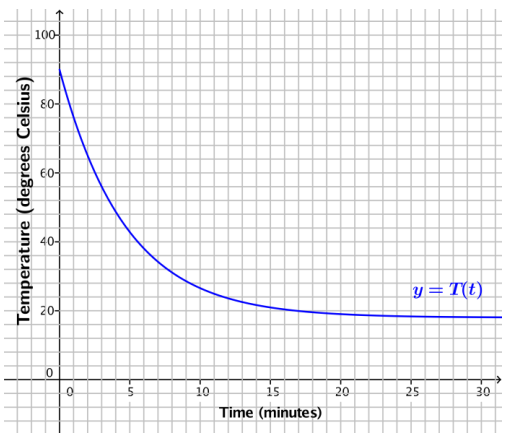
d. Use the graph of T to describe how the temperature decreases over time.
Answer:
Because the temperature is decreasing exponentially, the temperature drops rapidly at first and then slows down. After about 25 minutes, the temperature of the tea levels off.
e. Use properties of exponents to rewrite the temperature function in the form T(t) = 18 + 72(1 + r)t.
Answer:
T(t) = 18 + 72 e-o.213t
= 18 + 72(e-o.213t)t
≈ 18 + 72(0.8082)t
≈ 18 + 72(1 – 0.1918)t
f. In Lesson 26, we saw that the value of r represents the percent change of a quantity that is changing according to an exponential function of the form f(t) = A(1 + r)t. Describe what r represents in the context of the cooling tea.
Answer:
The number r represents the percent change in the difference between the temperature of the tea and the temperature of the room. Because r = -0.1918, the temperature difference is decreasing by 19.18% each minute.
g. As more time elapses, what temperature does the tea approach? Explain using both the context of the problem and the graph of the function T.
Answer:
The temperature of the tea approaches 18°C. Within the context of the problem, this makes sense because that is the ambient temperature (the outside temperature), so when the tea reaches 18°C Stops cooling. Looking at the expression of the function T, we see that as t → ∞, (0.8082)t → 0, so T → 18.
Mathematical Modeling Exercise 3:
Two thermometers are sitting in a room that is 22°C. When each thermometer reads 22°C, the thermometers are placed in two different ovens. Data for the temperatures T1 and T2 of these thermometers (in °C) t minutes after being placed in the oven is provided below.
Thermometer 1:

Thermometer 2:
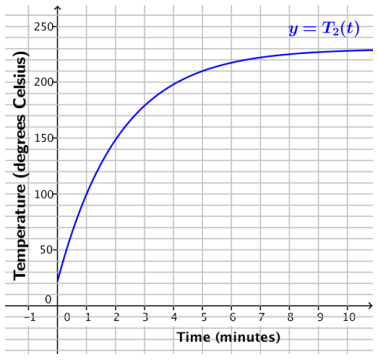
a. Do the table and graph given for each thermometer support the statement that Newton’s law of cooling also applies when the surrounding temperature is warmer? Explain.
Answer:
Yes. The graph shows a reflected exponential curve, which would indicate that a similar formula could be used. From both the table and the graph, it can be seen that the temperature increases rapidly at first and then levels off to the temperature of its surroundings; this coincides with what happens when an object is cooling (i.e., the temperature decreases rapidly and then levels off).
b. Which thermometer was placed in a hotter oven? Explain.
Answer:
Thermometer 2 was placed in a hotter oven. The graph shows its temperature leveling off at approximately 230°C, while the table indicates that thermometer I level off at approximately 176°C.
c. Using a generic decay constant, k, without finding Its value, write an equation for each thermometer expressing the temperature as a function of time.
Answer:
Thermometer 1: T1(t) = 176 + (22 – 176)e-kt
Thermometer 2: T2(t) = 230 + (22 – 230)e-kt
d. How do the equations differ when the surrounding temperature is warmer than the object rather than cooler as in previous examples?
Answer:
In the case where we are placing a cool object into a warmer space, the coefficient in front of the exponential expression is negative rather than positive.
e. How do the graphs differ when the surrounding temperature is warmer than the object rather than cooler as in previous examples?
Answer:
In the case where we are placing a cool object into a warmer space, the function increases rather than decreases.
Eureka Math Algebra 2 Module 3 Lesson 28 Problem Set Answer Key
Question 1.
Experiments with a covered cup of coffee show that the temperature (in degrees Fahrenheit) of the coffee can be modeled by the following equation:
f(t) = 112e-0.08t + 68,
where the time is measured in minutes after the coffee was poured into the cup.
a. What is the temperature of the coffee at the beginning of the experiment?
Answer:
180°F
b. What is the temperature of the room?
Answer:
68°F
c. After how many minutes is the temperature of the coffee 140°F? Give your answer to 3 decimal places.
Answer:
5.523 minutes
d. What is the temperature of the coffee after a few hours have elapsed?
Answer:
The temperature is slightly above 68°F.
e. What is the percent rate of change of the difference between the temperature of the room and the temperature of the coffee?
Answer:
f(t) = 112(e-0.08t) + 68
= 112(e-0.08)t + 68
≈ 112(0.9231)t + 68
≈ 112(1 – 0.0769)t + 68
Thus, the percent rate of change of the temperature difference is a decrease of 7.69% each minute.
Question 2.
Suppose a frozen package of hamburger meat is removed from a freezer that is set at 0°F and placed In a refrigerator that is set at 38°F. Six hours after being placed in the refrigerator, the temperature of the meat is 12°F.
a. Determine the decay constant, k.
Answer:
k = 0.063
b. Write a function for the temperature of the meat, T in Fahrenheit, as a function of time, t in hours.
Answer:
T(t) = 38 – 38e-0.063t
c. Graph the function T.
Answer:
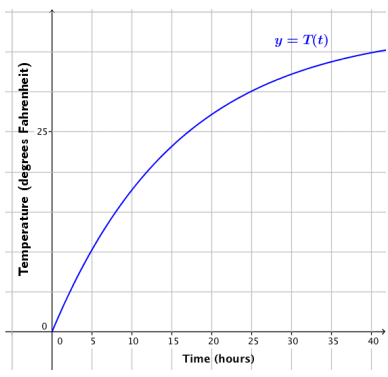
d. Describe the transformations required to graph the function T beginning with the graph of the natural exponential function f(t) = et.
Answer:
The graph is stretched horizontally, reflected across the y-axis, stretched vertically, reflected across the x-axis, and translated up.
e. How long will it take the meat to thaw (reach a temperature above 32°F)? Give answer to three decimal places.
Answer:
29.299 hours
f. What is the percent rate of change of the difference between the temperature of the refrigerator and the temperature of the meat?
Answer:
T(t) = 38 – 38e-0.063t
≈ 38 – 3 8(0.9389)t
≈ 38 – 38(1 – 0.01)t
So, the percent rate of change in the difference of temperature is 6.11%.
Question 3.
The table below shows the temperature of a pot of soup that was removed from the stove at time t = 0.

a. What is the initial temperature of the soup?
Answer:
100°C
b. What does the ambient temperature (room temperature) appear to be?
Answer:
20°C
c. Use the temperature at t = 10 minutes to find the decay constant, k.
Answer:
k = 0.173
d. Confirm the value of k by using another data point from the table.
Answer:
T(40) = 20 + 80e-0.17340 ≈ 20.079
e. Write a function for the temperature of the soup (in Celsius) as a function of time In minutes.
Answer:
T(t) = 20 + 80e-0.173t
f. Graph the function T.
Answer:
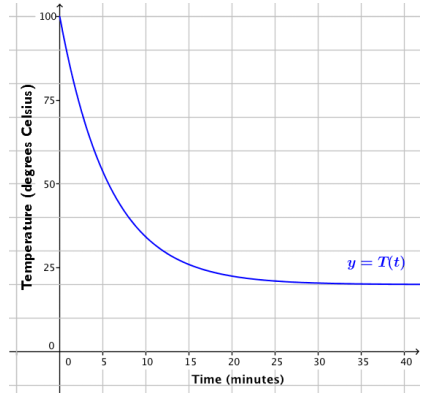
Question 4.
Match each verbal description with its correct graph and write a possible equation expressing temperature as a function of time.
(i) 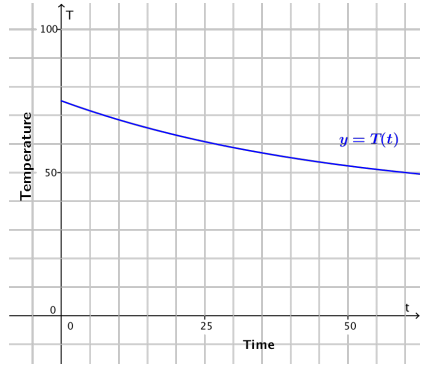
(ii) 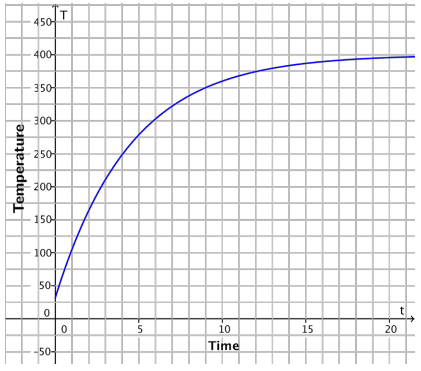
(iii) 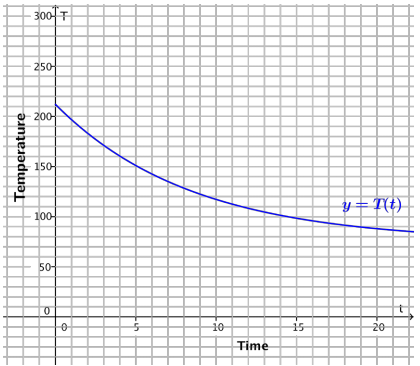
a. A pot of liquid is heated to a boil and then placed on a counter to cool.
Answer:
(iii), T(t) = 75 + (212 – 75)e-kt (Equations will vary.)
b. A frozen dinner is placed in a preheated oven to cook.
Answer:
(ii), T(t) = 400 + (32 – 400)e-kt (Equations will vary.)
c. A can of room-temperature soda is placed in a refrigerator.
Answer:
(i), T(t) = 40+ (75 – 40)e-kt (Equations will vary.)
Eureka Math Algebra 2 Module 3 Lesson 28 Exit Ticket Answer Key
Question 1.
A pizza, heated to a temperature of 400° Fahrenheit, is taken out of an oven and placed in a 75°F room at time t = 0 minutes. The temperature of the pizza is changing such that its decay constant, k, is 0.325. At what time is the temperature of the pizza 150°F and, therefore, safe to eat? Give your answer in minutes.
Answer:
T(t) = 75 + (400 – 75)e-0.325t = 150
325e-0.325t = 75
e-0.325t = \(\frac{75}{325}\)
-0.325 = ln(\(\frac{75}{325}\))
t ≈ 4.512
The pizza will reach 150°F after approximately 4\(\frac{1}{2}\) minutes.