Engage NY Eureka Math Algebra 2 Module 3 Lesson 18 Answer Key
Eureka Math Algebra 2 Module 3 Lesson 18 Opening Exercise Answer Key
Opening Exercise:
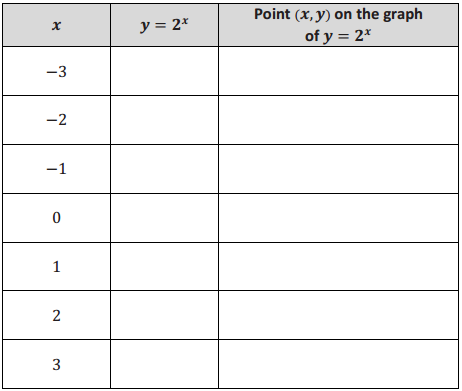
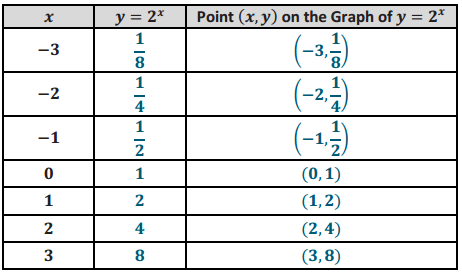
Complete the following table of values of the function f(x) = 2x. We want to sketch the graph of y f(x) and then reflect that graph across the diagonal line with equation y = x.
Answer:
On the set of axes below, plot the points from the table and sketch the graph of y = 2x. Next, sketch the diagonal line with equation y = x, and then reflect the graph of y = 2x across the line.
Answer:
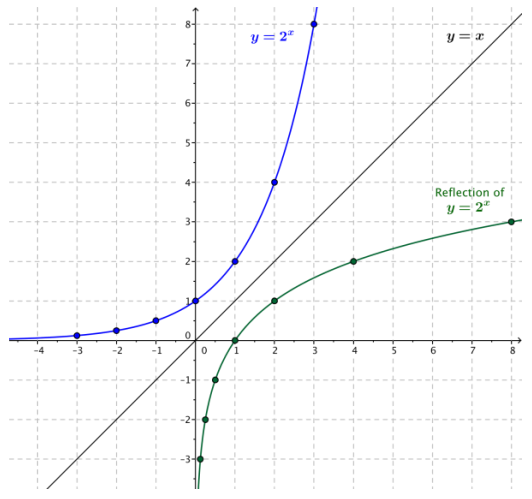
Eureka Math Algebra 2 Module 3 Lesson 18 Exercise Answer Key
Exercises:
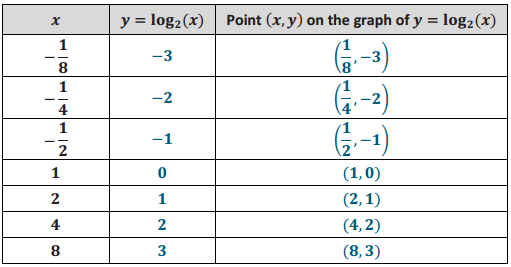
Exercise 1.
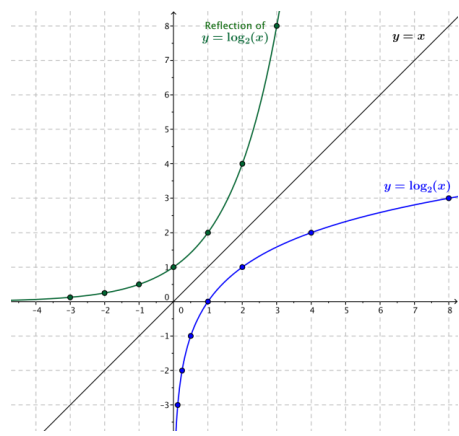
Complete the following table of values of the function g(x) = log2(x). We want to sketch the graph of y = g(x) and then reflect that graph across the diagonal line with equation y = x.
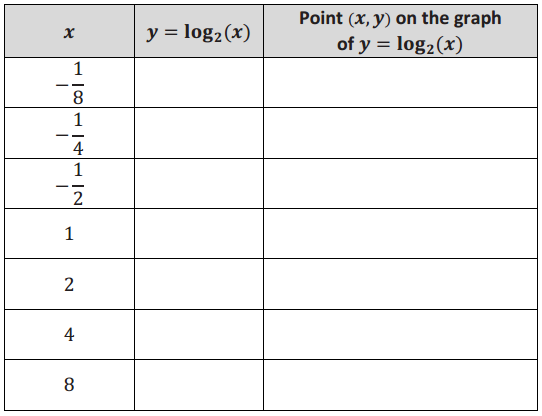
Answer:
On the set of axes below, plot the points from the table and sketch the graph of y = log2(x). Next, sketch the diagonal line with equation y = x, and then reflect the graph of y = log2(x) across the line.
Answer:
Exercise 2.
Working independently, predict the relation between the graphs of the functions f(x) = 3x and g(x) = log3(x). Test your predictions by sketching the graphs of these two functions. Write your prediction in your notebook, provide justification for your prediction, and compare your prediction with that of your neighbor.
Answer:
The graphs will be reflections of each other about the diagonal.
Exercise 3.
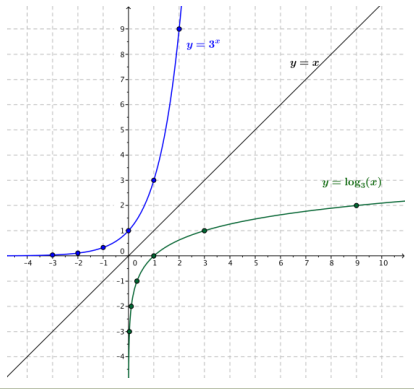
Now let’s compare the graphs of the functions f2(x) = 2 and f3(x) = 3. Sketch the graphs of the two exponential functions on the same set of axes; then, answer the questions below.
Answer:
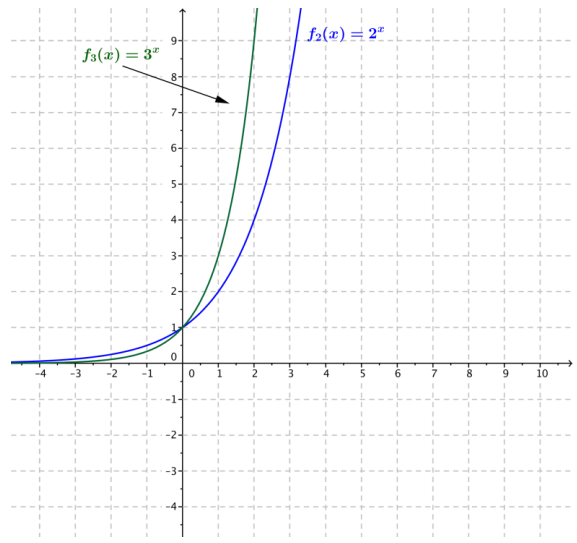
a. Where do the two graphs intersect?
Answer:
The two graphs intersect at the point (0, 1).
b. For which values of x is 2x < 3x?
Answer:
If x > 0, then 2x < 3x
c. For which values of x is 2x > 3x?
Aans:
If x < 0, then 2x > 3x
d. What happens to the values of the functions 12 and 13 as x → ∞?
Answer:
As x → ∞, both f2(x) → ∞‚ and f3(x) → ∞.
e. What happens to the values of the functions 12 and 13 as x → -∞?
Answer:
As x → -∞,both f2(x) → 0 and f3(x) → 0.
f. Does either graph ever intersect the x-axis? Explain how you know.
Answer:
No. For every value of x, we know 2x ≠ 0 and 3x ≠ 0.
Exercise 4.
Add sketches of the two logarithmic functions g2(x) = log2(x) and g3(x) = log3(x) to the axes with the graphs of the exponential functions from Exercise 3; then, answer the questions below.
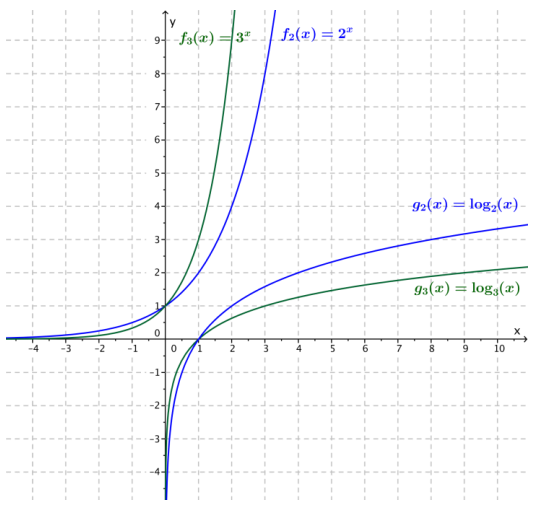
a. Where do the two logarithmic graphs intersect?
Answer:
The two graphs intersect at the point (1, 0).
b. For which values of x is log2(x) < log3(x)?
Answer:
If x < 1, then log2(x) < log3(x).
c. For which values of x is log2(x) > log3(x)?
Answer:
If x > 1, then log2(x) > log3(x).
d. What happens to the values of the functions g2 and g3 as x → ∞?
Answer:
As x → ∞, both g2(x) → ∞ and g3(x) → ∞.
e. What happens to the values of the functions g2 and g3 as x → 0?
Answer:
As x → 0, both g2(x) → -∞ and g3(x) → -∞.
f. Does either graph ever intersect the y-axis? Explain how you know.
Answer:
No. Logarithms are only defined for positive values of x.
g. Describe the similarities and differences in the behavior of f2(x) and g2(x) as x → ∞.
Answer:
As x → ∞, both f2(x) → ∞ and g2(x) → ∞; however, the exponential function gets very large very quickly, and the logarithmic function gets large rather slowly.
Eureka Math Algebra 2 Module 3 Lesson 18 Problem Set Answer Key
Question 1.
Sketch the graphs of the functions f(x) = 5x and g(x) = log5(x).
Answer:
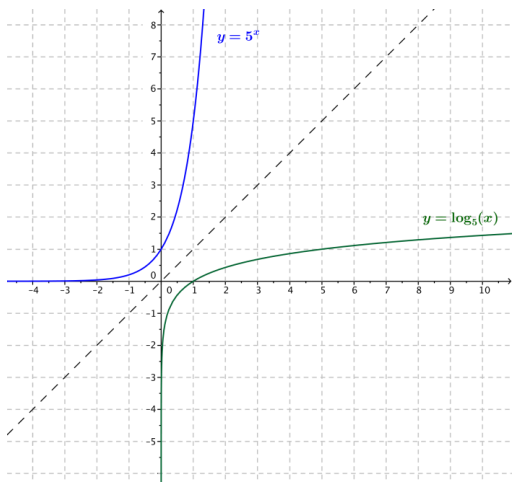
Question 2.
Sketch the graphs of the functions f(x) = (\(\frac{1}{2}\))x and g(x) = log\(\frac{1}{2}\)(x).
Answer:
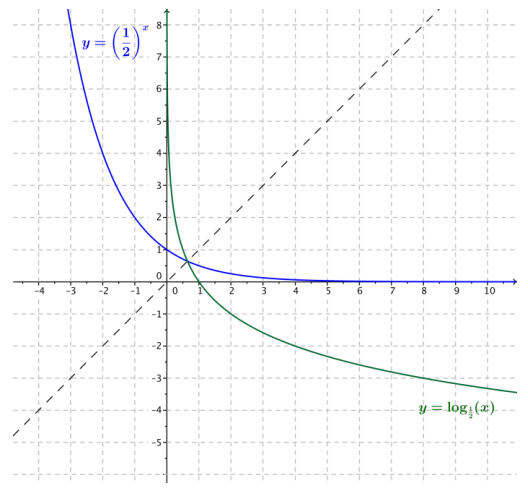
Question 3.
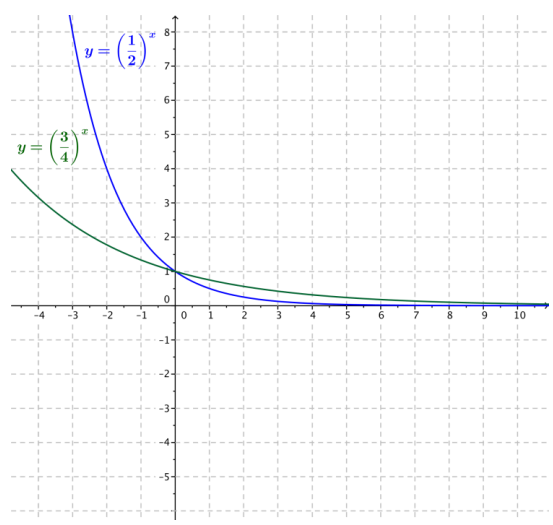
Sketch the graphs of the functions f1(x) = (\(\frac{1}{2}\))x and f2(x) = (\(\frac{3}{4}\))x on the same sheet of graph paper, and answer the following questions.
a. Where do the two exponential graphs intersect?
Answer:
The graphs intersect at the point (0, 1).
b. For which values of x is (\(\frac{1}{2}\))x < (\(\frac{3}{4}\))x?
Answer:
If x > 0, then (\(\frac{1}{2}\))x < (\(\frac{3}{4}\))x.
c. For which values of x is (\(\frac{1}{2}\))x > (\(\frac{3}{4}\))x??
Answer:
If x < 0, then (\(\frac{1}{2}\))x < (\(\frac{3}{4}\))x.
d. What happens to the values of the functions f1 and f2 as x → ∞?
Answer:
As x → ∞,both f1(x) → 0 and f2(x) → 0.
e. What are the domains of the two functions f1 and f2?
Answer:
Both functions have domain (-∞, ∞).
Question 4.
Use the information from Problem 3 together with the relationship between graphs of exponential and logarithmic functions to sketch the graphs of the functions g1(x) = log\(\frac{1}{2}\)(x) and g2(x) = log>\(\frac{3}{4}\)</(x) on the same sheet of graph paper. Then, answer the following questions.
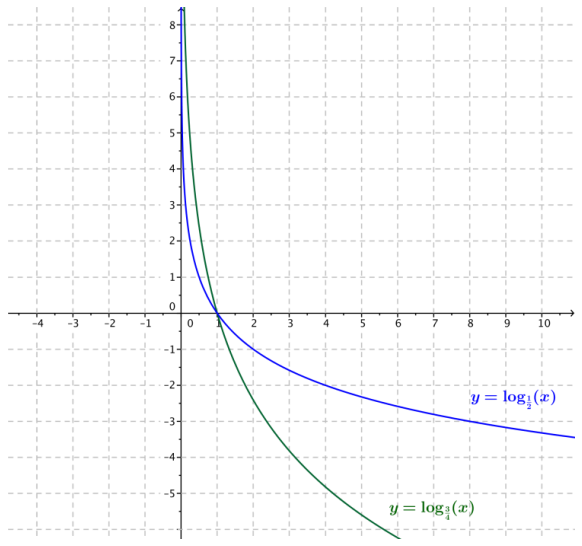
a. Where do the two logarithmic graphs intersect?
Answer:
The graphs intersect at the point (1, 0).
b. For which values of x is log\(\frac{1}{2}\)(x) < log\(\frac{3}{4}\)(x)?
Answer:
When x < 1, we have log\(\frac{1}{2}\)(x) < log\(\frac{3}{4}\)(x).
c. For which values of x is log\(\frac{1}{2}\)(x) > log\(\frac{3}{4}\)(x)?
Answer:
When x > 1, we have log\(\frac{1}{2}\)(x) > log\(\frac{3}{4}\)(x).
d. What happens to the values of the functions g1 and g2 as x → ∞?
Answer:
As x → ∞, both g1(x) → -∞ and g2(x) → -∞.
e. What are the domains of the two functions g1 and g2?
Answer:
Both functions have domain (0, ∞).
Question 5.
For each function f, find a formula for the function h in terms of x.
a. If f(x) = x3, find h(x) = 128f(\(\frac{1}{4}\)x) + f(2x).
Answer:
h(x) = 10x3
b. If (x) = x2 + 1, find h(x) = f(x + 2) – f(2).
Answer:
h(x) = x2 + 4x
c. If f(x) = x3 + 2x2 + 5x + 1, find h(x) = \(\frac{f(x)+f(-x)}{2}\)
Answer:
h(x) = 2x2 + 1
d. If (x) = x3 + 2x2 + 5x + 1, find h(x) = \(\frac{f(x)-f(-x)}{2}\)
Answer:
h(x) = x3 + 5x
Question 6.
In Problem 5, parts (c) and (d), list at least two aspects about the formulas you found as they relate to the function f(x) = x3 + 2x2 + 5x + 1.
Answer:
The formula for 1(c) is all of the even power terms off. The formula for 1(d) is all of the odd power terms off. The sum of the two functions gives f back again; that is, \(\frac{f(x)+f(-x)}{2}\) + \(\frac{f(x)-f(-x)}{2}\) = f
Question 7.
For each of the functions f and g below, write an expression for (i) f(g(x)), (ii) g(f(x)) and (iii) f(f(x)) in terms of x.
a. f(x) = x\(\frac{2}{3}\), g(x) = x12
Answer:
i. f(g(x)) = x8
ii. g(f(x)) = x8
iii. f(f(x)) = x\(\frac{4}{9}\)
b. f(x) = \(\frac{\boldsymbol{b}}{x-a}\), g(x) = \(\frac{\boldsymbol{b}}{\boldsymbol{x}}\) + a for two numbers a and b, when x is not 0 or a.
Answer:
i. f(g(x)) = x
ii. g(f(x)) = x
iii. f(f(x)) = \(\frac{b}{\frac{b}{x-a}-a}\), which is equivalent to f(f(x)) = \(\frac{b(x-a)}{b+a^{2}-a x}\)
c. f(x) = \(\frac{x+1}{x-1}\) g(x) = \(\frac{x+1}{x-1}\) when x is not 1 or -1
Answer:
i. f(g(x)) = x
ii. g(f(x)) = x
iii. f(f(x)) = x
d. f(x) = 2x, 9(x) = log2(x)
Answer:
i. f(g(x)) = x
ii. g(f(x)) = x
iii. f(f(x)) = x
e. f(x) = ln(x), g(x) = ex
Answer:
i. f(g(x)) = x
ii. g(f(x)) = x
iii. f(f(x)) = ln(ln(x))
f. f(x) = 2 . 100x, g(x) = \(\frac{1}{2}\)log(\(\frac{1}{2}\)x)
Answer:
i. f(g(x)) = x
ii. g(f(x)) = x
iii. f(f(x)) = 2 . 10000100x
Eureka Math Algebra 2 Module 3 Lesson 18 Exit Ticket Answer Key
Question 1.
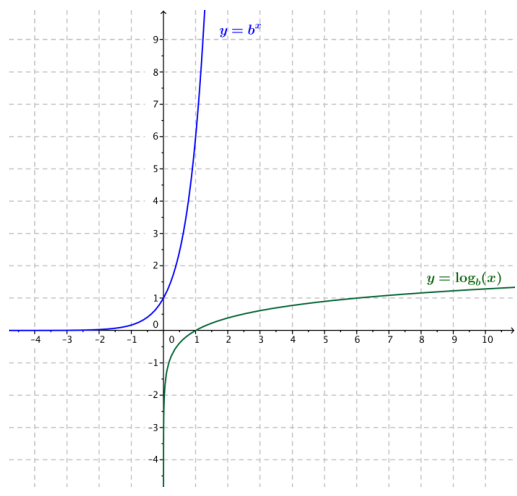
The graph of a logarithmic function g(x) = logb(x) is shown below.
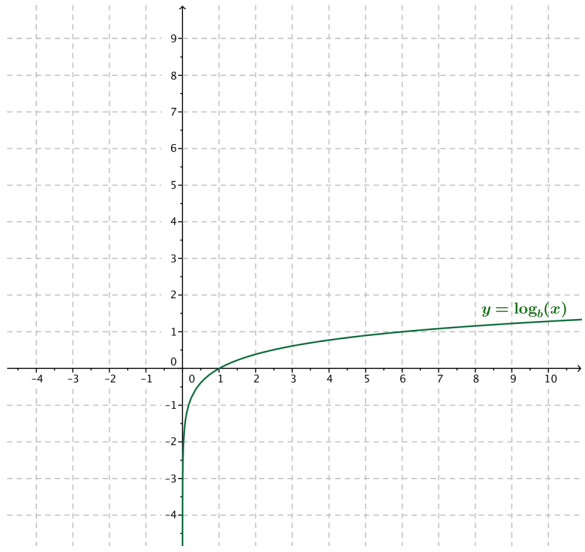
a. Explain how to find points on the graph of the function f(x) = bx
Answer:
A point (x, y) is on the graph of f if the corresponding point (y, x) is on the graph of g.
b. Sketch the graph of the function f(x) = bx on the same axes.
Answer: