Engage NY Eureka Math Algebra 2 Module 3 Lesson 1 Answer Key
Eureka Math Algebra 2 Module 3 Lesson 1 Opening Exercise Answer Key
Opening Exercise:
Exercise 1.
Can you fold a piece of notebook paper in half 10 times?
Answer:
Answers will vary. Although incorrect, many students may initially answer “Yes.”
Exercise 2.
How thick will the folded paper be?
Answer:
Answers will vary. The following is a typical student guess: It will be about 1 cm.
Exercise 3.
Will the area of the paper on the top of the folded stack be larger or smaller than a postage stamp?
Answer:
Iit will be smaller because I will be dividing the rectangle in half 10 times, and since a piece of paper is about 8.5 in. by 11 in., it will be very small when divided in half that many times.
Exploratory Challenge:
a. What are the dimensions of your paper?
Answer:
The dimensions are 8.5 in. by 11 in.
b. How thick is one sheet of paper? Explain how you decided on your answer.
Answer:
A ream of paper is 500 sheets. It is about 2 in. high. Dividing 2 by 500 would give a thickness of a piece of paper to be approximately 0.004 in.
c. Describe how you folded the paper.
Answer:
First, we folded the paper in half so that it was 8.5 in. by 5.5 in.; then, we rotated the paper and folded it again so that it was 5.5 in. by 4.25 in.; then, we rotated the paper and folded it again, and so on.
d. Record data in the following table based on the size and thickness of your paper.

Answer:
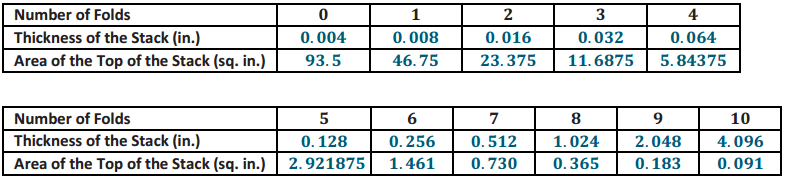
Answers are rounded to three decimal places after the fifth fold.
e. Were you able to fold a piece of notebook paper in half 10 times? Why or why not?
Answer:
No. It got too small and too thick for us to continue folding it.
f. Create a formula that approximates the height of the stack after n folds.
Answer:
Our formula is H(n) = T 2n, where T is the thickness of the paper and H(n) is the height after n folds. In this case, T = 0.004 in.
g. Create a formula that will give you the approximate area of the top after n folds.
Answer:
Our formula is A(n) = A0\(\left(\frac{1}{2}\right)^{n}\), where A0 is the area of the original piece of paper and A(n) is the area of the top after n folds. In this case, A0 = 93.5 sq. in.
h. Answer the original questions from the Opening Exercise. How do the actual answers compare to your original predictions?
Answer:
It was impossible to fold the paper more than 7 times. Using our model, if we could fold the paper 10 times, it would be just over 4 in. thick and less than \(\frac{1}{10}\) sq.in., which is much smaller than the area of a postage stamp. Our predictions were inaccurate because we did not consider how drastically the sizes change when successively doubling or having measurements.
Eureka Math Algebra 2 Module 3 Lesson 1 Example Answer Key
Example 1: Using the Properties of Exponents to Rewrite Expressions
The table below displays the thickness and area of a folded square sheet of gold foil. In 2001, Britney Gallivan, a California high school junior, successfully folded a 100-square-inch sheet of gold foil in half 12 times to earn extra credit in her mathematics class.
Rewrite each of the table entries as a multiple of a power of 2.
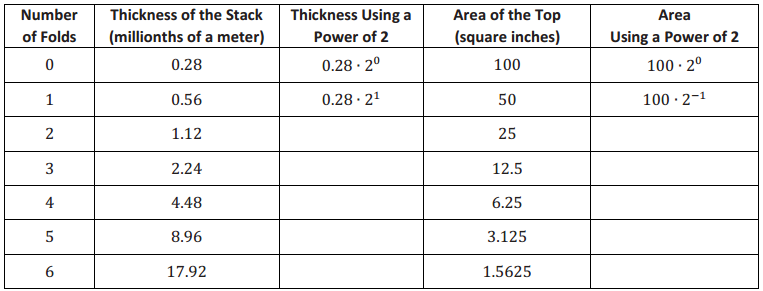
Answer:
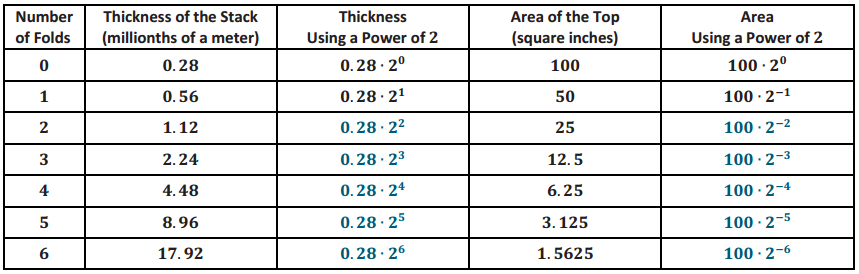
Example 2: Applying the Properties of Exponents to Rewrite Expressions.
Rewrite each expression in the form kxn, where k is a real number, n is an integer, and x is a nonzero real number.
a. (5x5) (-3x2)
Answer:
Method 1: Apply the definition of an exponent and properties of algebra.
(5x5) . (-3x2) = 5. -3x5. x2 = -15 (x . x . x . x . x)(x . x) = -15x7
Method 2: Apply the rules of exponents and the properties of algebra.
5x5 – 3x2 = 5 . -3 x5 . x2 = -15 . x5+2 = -15x7
b. \(\frac{3 x^{5}}{(2 x)^{4}}\)
Answer:
Method 1: Apply the definition of an exponent and properties of algebra.

Method 2: Apply the rules of exponents and the properties of algebra.
\(\frac{3 x^{5}}{(2 x)^{4}}\) = \(\frac{3}{16}\) x5 – 4 = \(\frac{3}{16}\)x
c. \(\frac{3}{\left(x^{2}\right)^{-3}}\)
Answer:
Method 1: Apply the definition of an exponent and properties of algebra.

Method 2: Apply the rules of exponent and the properties of algebra.
\(\frac{3}{\left(x^{2}\right)^{-3}}\) = \(\frac{3}{x^{2(-3)}}=\frac{3}{x^{-6}}\) = 36.
d. \(\frac{x^{-3} x^{4}}{x^{8}}\)
Answer:
Method 1: Apply the definition of an exponent and properties of algebra.

Method 2: Apply the rules of exponents and the properties of algebra.
\(\frac{x^{-3} x^{4}}{x^{8}}\) = \(\frac{x^{-3+4}}{x^{8}}=\frac{x^{1}}{x^{8}}\) = x1 – 8 = x-7
Eureka Math Algebra 2 Module 3 Lesson 1 Exercise Answer Key
Exercises 1 – 5:
Rewrite each expression in the form kxn, where k is a real number and n is an integer. Assume x ≠ 0.
Exercise 1.
2x5 . x10
Answer:
2x15
Exercise 2.
\(\frac{1}{3 x^{8}}\)
Answer:
\(\frac{1}{3}\) x-8
Exercise 3.
\(\frac{6 x^{-5}}{x^{-3}}\)
Answer:
6x-5-(-3) = 6x-2
Exercise 4.
\(\left(\frac{3}{x^{-22}}\right)^{-3}\)
Answer:
(3x22)-3 = 3-3 x-66 = \(\frac{1}{27}\) x-66
Exercise 5.
(x2)n . x3
Answer:
x2n . x3 = x2n + 3
Eureka Math Algebra 2 Module 3 Lesson 1 Problem Set Answer Key
Question 1.
Suppose your class tried to fold an unrolled roll of toilet paper. It was originally 4 in. wide and 30 ft. long. Toilet paper is approximately 0.002 in. thick.
a. Complete each table, and represent the area and thickness using powers of 2.
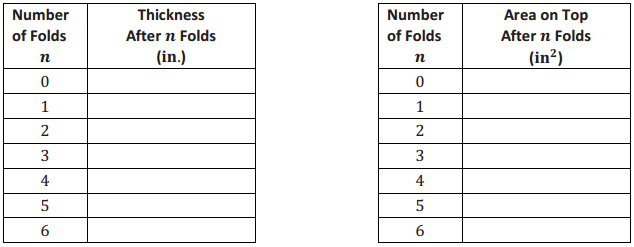
Answer:
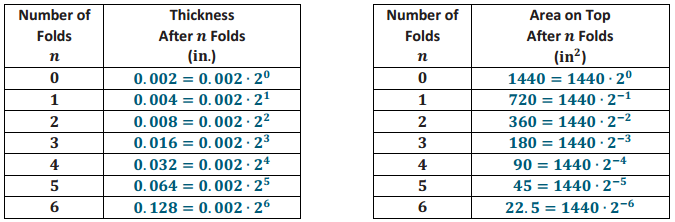
b. Create an algebraic function that describes the area in square inches after n folds.
Answer:
A(n) = 1440 . 2-n where n is a nonnegative integer.
c. Create an algebraic function that describes the thickness in inches after n folds.
Answer:
T(n) = 0.002 . 2n, where n is a nonnegative integer.
Question 2.
In the Exit Ticket, we saw the formulas below. The first formula determines the minimum width, W, of a square piece of paper of thickness T needed to fold it in half n times, alternating horizontal and vertical folds. The second formula determines the minimum length, L, of a long rectangular piece of paper of thickness T needed to fold it In half n times, always folding perpendicular to the long side.
W = π . T . \(2^{\frac{3(n-1)}{2}}\)
L = \(\frac{\pi T}{6}\) (2n + 4) (2n – 1)
Use the appropriate formula to verify why It is possible to fold a 10 inch by 10 inch sheet of gold foil in half 13 times. Use 0. 28 millionth of a meter for the thickness of gold foil.
Answer:
Given that the thickness of the gold foil is 0.28 millionth of a meter, we have
\(\frac{0.28}{1,000,000} \mathrm{~m} \cdot \frac{100 \mathrm{~cm}}{1 \mathrm{~m}}\) = 0.000028 cm . \(\frac{1 \mathrm{in}}{2.54 \mathrm{~cm}}\) = 0.00001102 in.
Using the formula
W = π T \(2^{\frac{3(n-1)}{2}}\)
with n = 13 and T = 0.00001102, we get
W = π(0.00001102)2\(\frac{3(13-1)}{2}\) ≈ 9.1
Thus, any square sheet of gold foil larger than 9.1 inches by 9.1 inches can be folded in half 13 times, so a 10 inch by 10-inch sheet of gold foil can be folded in half 13 times.
Question 3.
Use the formula from Problem 2 to determine if you can fold an unrolled roll of toilet paper In half more than 10 times. Assume that the thickness of a sheet of toilet paper is approximately 0.002 in. and that one roll is 102 ft. long.
Answer:
First, convert feet to inches. 102 ft. = 1224 in.
Then, substitute 0.002 and 10 into the formula for T and n, respectively.
L = \(\frac{\pi(0.002)}{6}\) (210 + 4) (210 – 1) = 1101.3
The roll is just long enough to fold in half 10 times.
Question 4.
Apply the properties of exponents to rewrite each expression in the form kxn, where n is an integer and x ≠ 0.
a. (2x3) (3x5) (6x)2
Answer:
2 . 3 . 36x3 + 5 + 2 = 216x10
b. \(\frac{3 x^{4}}{(-6 x)^{-2}}\)
Answer:
3x4 . 36x2 = 108x6
c. \(\frac{x^{-3} x^{5}}{3 x^{4}}\)
Answer:
\(\frac{1}{3}\) x-3 + 5 – 4 = \(\frac{1}{3}\)x-2
d. 5(x3)-3 (2x)-4
Answer:
\(\frac{5}{16}\) x-9 + (-4) = \(\frac{5}{16}\) x-13
e. \(\left(\frac{x^{2}}{4 x^{-1}}\right)^{-3}\)
Answer:
\(\frac{x^{-6}}{4^{-3} x^{3}}\) = 64x-6-3 = 64x-9
Question 5.
Apply the properties of exponents to verify that each statement is an identity.
a. \(\frac{2^{n+1}}{3^{n}}=2\left(\frac{2}{3}\right)^{n}\) for integer values of n.
Answer:
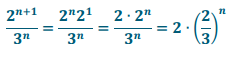
b. 3n + 1 – 3n = 2 . 3n for integer values of n
Answer:
3n + 1 – 3n = 3n . 31 – 3n
= 3n(3 – 1) = 3n . 2 = 2 . 3n
c. \(\frac{1}{\left(3^{n}\right)^{2}} \cdot \frac{4^{n}}{3}=\frac{1}{3}\left(\frac{2}{3}\right)^{2 n}\)
for integer values of n.
Answer:

Question 6.
Jonah was trying to rewrite expressions using the properties of exponents and properties of algebra for nonzero values of x. In each problem, he made a mistake. Explain where he made a mistake in each part, and provide a correct solution.
Jonah’s Incorrect Work
a. (3x2)-3 = -9x-6
b. \(\frac{2}{3 x^{-5}}\) = 6x5
c. \(\frac{2 x-x^{3}}{3 x}\) = \(\frac{2}{3}\) – x3
In part (a), he multiplied 3 by the exponent -3. The correct solution is 3-3 x-6 = \(\frac{1}{27}\) x-6
In part (b), he multiplied 2 by 3 when he rewrote x-5. The 3 should remain in the denominator of the expression. The correct solution is \(\frac{2}{3}\)x5.
In port (c), he only divided the first term by 3x, but he should have divided both terms by 3x. The correct solution
is \(\frac{2 x}{3 x}-\frac{x^{3}}{3 x}=\frac{2}{3}-\frac{x^{2}}{3}\)
Question 7.
If x = 5a4 and a = 2b3, express x in terms of b.
Answer:
By the substitution property, if x = 5a4 and a = 2b3, then x = 5(2b3)4. Rewriting the right side in an equivalent
form gives x = 80b12.
Question 8.
If a = 2b3 and b = –\(\frac{1}{2}\)c-2 ,express x in terms of c.
Answer:
By the substitution property, if a = 2b3 and b = –\(\frac{1}{2}\)c-2, then a = 2 (-\(\frac{1}{2}\) c-2)3. Rewriting the right side in an equivalent form gives a = –\(\frac{1}{4}\) c-6.
Question 9.
If x = 3y4 and y = \(\frac{s}{2 x^{3}}\), show that s = 54y13.
Answer:
Rewrite the equation y = \(\frac{s}{2 x^{3}}\) to isolate the variable s.
y = \(\frac{s}{2 x^{3}}\)
2x3 = s
By the substitution property, if s = 2x3y and x = 3y4, then s = 2(3y4)3 . y. Rewriting the right side in an equivalent form gives s = 2 27y12 . y = 54y13.
Question 10.
Do the following tasks without a calculator.
a. Express 83 as a power of 2.
Answer:
83= (23)3 = 29
b. Divide 415 by 210.
Answer:
\(\frac{4^{15}}{2^{10}}=\frac{2^{30}}{2^{10}}=2^{20}\) or
\(\frac{4^{15}}{2^{10}}=\frac{4^{15}}{4^{5}}=4^{10}\)
Question 11.
Use powers of 2 to perform each calculation without a calculator or other technology.
a. \(\frac{2^{7} \cdot 2^{5}}{16}\)
Answer:
\(\frac{2^{7} \cdot 2^{5}}{16}\) = \(\frac{2^{7} \cdot 2^{5}}{2^{4}}\) = 27 + 5 -4 = 28 = 256
b. \(\frac{512000}{320}\)
Answer:
\(\frac{512000}{320}\) = \(\frac{512 \cdot 1000}{32 \cdot 10}=\frac{2^{9}}{2^{5}}\) . 100 = 24 . 100 = 1600
Question 12.
Write the first five terms of each of the following recursively defined sequences:
a. an + 1 = 2an, a1 = 3
Answer:
3, 6, 12, 24, 48
b. an + 1 = (an)2 a1 = 3
Answer:
3, 9, 81, 6561, 43 046 721
c. an + 1 = 2(an)232, a1 = x, where x is a real number Write each term in the form n.
Answer:
x, 2x2, 8x4, 128x8, 32768x16
d. an + 1 = 2(an)-1, a1 = y, (y ≠ 0) Write each term in the form kxn.
Answer:
y, 2y-1, y, 2y-1, y
Question 13.
In Module 1, you established the identity (1 – r)(1 + r + r2 + …… + rn – 1) = 1 – rn, where r is a real number and n is a positive integer.
Use this identity to respond to parts (a)-(g) below.
a. Rewrite the given identity to isolate the sum 1 + r + r2 + …… + rn – 1 for r ≠1.
Answer:
(1 + r + r2 +….. + rn – 1) = \(\frac{1-r^{n}}{1-r}\)
b. Find an explicit formula for 1 + 2 + 22 + 23 + ……… + 210.
Answer:
\(\frac{1-2^{11}}{1-2}\) = 211 – 1
c. Find an explicit formula for 1 + a + a2 + a3 + ………. + a10 in terms of powers of a.
Answer:
\(\frac{1-a^{11}}{1-a}\)
d. Jerry simplified the sum 1 + a + a2 + a3 + a4+ a5 by writing 1 + a15. What did he do wrong?
Answer:
He assumed that when you add terms with the same base, you also add the exponents. You only add the exponents when you multiply terms with some base.
e. Find an explicit formula for 1 + 2a + (2a)2 + (2a)3 + …………. + (2a)12 in terms of powers of a.
Answer:
\(\frac{1-(2 a)^{13}}{1-2 a}\)
f. Find an explicit formula for 3 + 3(2a) + 3(2a)2 + 3(2a)3 + …….. + 3(2a)12 in terms of powers of a. Hint: Use part (e).
Answer:
3 . \(\left(\frac{1-(2 a)^{13}}{1-2 a}\right)\)
g. Find an explicit formula for P + P(1 + r) + P(1 + r))2) + P(1 + r))3) + …………… + P(1 + r))n – 1 in terms of powers of (1 + r).
Answer:
P . \(\left(\frac{1-(1+r)^{n}}{1-(1+r)}\right)\) = P . \(\left(\frac{1-(1+r)^{n}}{-r}\right)\)
Eureka Math Algebra 2 Module 3 Lesson 1 Exit Ticket Answer Key
The following formulas for paper folding were discovered by Britney Gallivan in 2001 when she was a high school junior. The first formula determines the minimum width, W, of a square piece of paper of thickness T needed to fold it in half n times, alternating horizontal and vertical folds. The second formula determines the minimum length, L, of a long rectangular piece of paper of thickness T needed to fold it in half n times, always folding perpendicular to the long side.
W = π . T . 2\(\frac{3(n-1)}{2}\)
L = \(\frac{\pi T}{6}\) (2n + 4) (2n – 1)
Question 1.
Notebook paper is approximately 0.004 in. thick. Using the formula for the width W, determine how wide a square piece of notebook paper would need to be to successfully fold it in half 13 times, alternating horizontal and vertical folds.
Answer:
The paper would need to be approximately 3,294.2 in. wide: W = π T 2\(\frac{3(13-1)}{2}\) = π (0.004)218 ≈ 3294.199.
Question 2.
Toilet paper is approximately 0.002 in. thick. Using the formula for the length L, how long would a continuous sheet of toilet paper have to be to fold it in half 12 times, folding perpendicular to the long edge each time?
Answer:
The paper would have to be approximately 17,581.92 in. long, which is approximately 0.277 mi.:
L = \(\left(\frac{\pi(\mathbf{0.002})}{6}\right)\) (212 + 4) (212 – 1) = π\(\frac{1}{3000}\) (4100) (4095) = 5596.5 π ≈ 17,581.92
Question 3.
Use the properties of exponents to rewrite each expression in the form kxn. Then, evaluate the expression for the given value of x.
a. 2x3 . \(\frac{5}{4}\)x-1; x = 2
Answer:
2(\(\frac{5}{4}\)) x3 x-1 = \(\frac{5}{2}\)x2
when x = 2, \(\frac{5}{2}\) x2 = \(\frac{5}{2}\) (2)2 = 10
b. \(\frac{9}{(2 x)^{-3}}\); x = –\(\frac{1}{3}\)
Answer:
\(\frac{9}{2^{-3} x^{-3}}\) = 72x3
when x = –\(\frac{1}{3}\), 72x3 = 72\(\left(-\frac{1}{3}\right)^{3}\) = –\(\frac{8}{3}\)