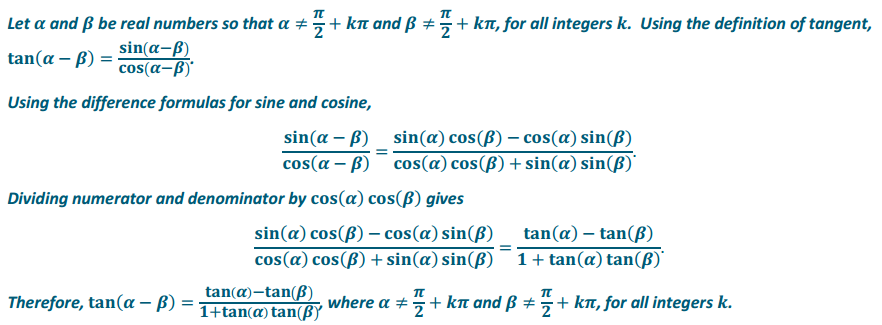Engage NY Eureka Math Algebra 2 Module 2 Lesson 17 Answer Key
Eureka Math Algebra 2 Module 2 Lesson 17 Example Answer Key
Examples 1 – 2: Formulas for sin(α + β) and cos(α + β)
Example 1.
One conjecture is that the formula for the sine of the sum of two numbers is sin(α + β) = sin(α) cos(β) + cos(α) sin(β). The proof can be a little long, but it is fairly straightforward. We will prove only the case when the two numbers are positive, and their sum is less than \(\frac{\pi}{2}\).
a. Let α and β be positive real numbers such that 0 < α + β < \(\frac{\pi}{2}\).
Answer:
b. Construct rectangle MNOP such that PR = 1,
m∠PQR = 90°, m∠RPQ = β and
m∠QPM = α. See the figure on the right.
Answer:
c. Fill in the blanks in terms of α and β:
i. m∠RPO = ________ .
Answer:
\(\frac{\pi}{2}\) – α – β
ii. m∠PRO = ________ .
Answer:
α + β
iii. Therefore, sin(α – β) = PO.
iv. RQ = sin(____).
Answer:
β
v. PQ = cos(___).
Answer:
β
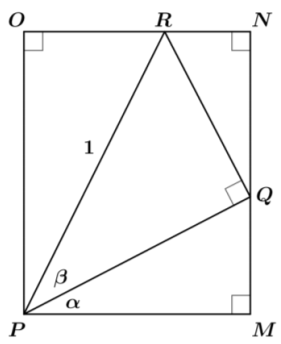
d. Let’s label the angle and length measurements as shown.
Answer:
e. Use this new figure to fill in the blanks in terms of α and β:
i. Why does sin(α) = \(\frac{M Q}{\cos (\beta)}\) ?
Answer:
The length of the hypotenuse of ∆ PQM is cos(β), and MQ is the length of the side opposite α.
ii. Therefore, MQ = ________ .
Answer:
sin(α)cos(β)
iii. m∠RQN = ________ .
Answer:
α
f. Now, consider ∆ RQN. Since cos(α) = \(\frac{Q N}{\sin (\beta)}\),
i. QN = ________ .
Answer:
cos(α) sin(β)
Example 2.
Now, let’s prove our other conjecture, which is that the formula for the cosine of the sum of two numbers is
cos(α + β) = cos(α) cos(β) – sin(α) sin(β).
Again, we will prove only the case when the two numbers are positive, and their sum is less than \(\frac{\pi}{2}\). This time, we will use the sine addition formula and identities from previous lessons instead of working through a geometric
proof.
Fill in the blanks in terms of α and β:
Let α and β be any real numbers. Then,
cos(α + β) = sin(\(\frac{\pi}{2}\)-(_______))
= sin(_______) – β)
= sin((_______) + (-β))
= sin(_______) cos(-β) + cos(_______) sin(-β)
= cos(α) cos(-β) + sin(α) sin(-β)
= cos(α) cos(β) – sin(α) sin(β).
Answer:
The completed proof should look like the following:
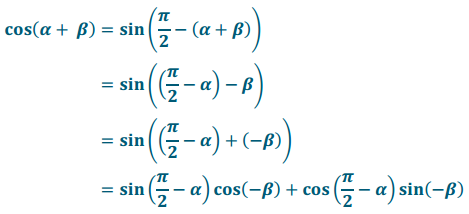
= cos(α) cos(-β) + sin(α) sin(-β)
= cos(α) cos(β) – sin(α) sin(β).
Eureka Math Algebra 2 Module 2 Lesson 17 Opening Exercise Answer Key
We have seen that sin(α + β) ≠ sin(α) + sin(β). So, what is sin(α + β)? Begin by completing the following table:
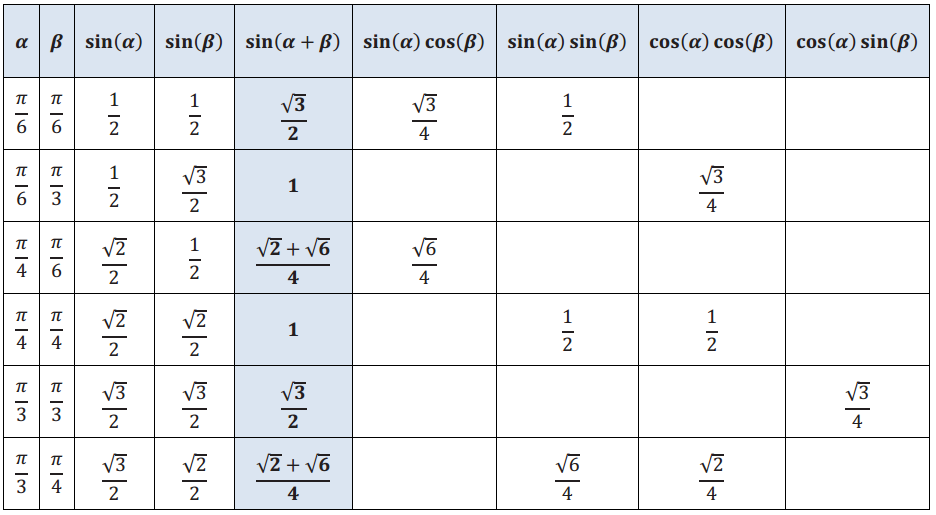
Answer:
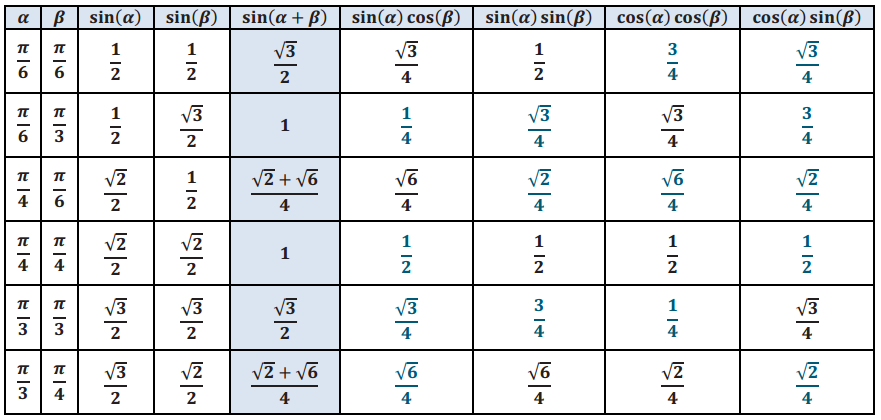
Eureka Math Algebra 2 Module 2 Lesson 17 Exercise Answer Key
Exercises 1 – 2: Formulas for sin(α – β) and cos(α – β)
Exercise 1.
Rewrite the expression sin(α – β) as sin(α + (-β)). Use the rewritten form to find a formula for the sine of the difference of two angles, recalling that the sine is an odd function.
Answer:
Let α and β be any real numbers. Then,
sin(α + (-β)) = sin(α) cos(-β) + cos(α) sin(-β)
= sin(α) cos(β) – cos(α) sin(β).
Therefore, sin(α – β) = sin(α) cos(β) – cos(α) sin(β) for all real numbers α and β.
Exercise 2.
Now, use the same idea to find a formula for the cosine of the difference of two angles. Recall that the cosine is an even function.
Answer:
Let α and β be any real numbers. Then,
cos(α – β) = cos(α + (-β))
= cos(α) cos(-β) – sin(α) sin(-β)
= cos(α) cos(β) + sin(α) sin(β).
Therefore, cos(α – β) = cos(α) cos(β) + sin(α) sin(β) for all real numbers α and β.
Exercise 3.
Derive a formula for tan(α + β) in terms of tan(α) and tan(β), where all of the expressions are defined.
Hint: Use the addition formulas for sine and cosine.
Answer:

Exercise 4.
Derive a formula for sin(2u) in terms of sin(u) and cos(u) for all real numbers u.
Answer:
Let u be any real number. Then, sin(2u) = sin(u + u) = sin(u)cos(u) + cos(u)sin(u), which is equivalent to sin(2u) = 2 sin(u) cos(u).
Therefore, sin(2u) = 2 sin(u) cos(u) for all real numbers u.
Exercise 5.
Derive a formula for cos(2u) in terms of sin(u) and cos(u) for all real numbers u.
Answer:
Let u be a real number. Then, cos(2u) cos(u + u) = cos(u) cos(u) – sin(u) sin(u), which is equivalent to
cos(2u) = cos2(u) – sin2(u).
Therefore, cos(2u) = cos2(u) – sin2(u) for all real numbers u. Using the Pythagorean identities, you can rewrite this identity as cos(2u) = 2 cos2(u) – 1 or as cos(2u) = 1 – 2 sin2(u) for all real numbers u.
Eureka Math Algebra 2 Module 2 Lesson 17 Problem Set Answer Key
Question 1.
Prove the formula
cos(α + β) = cos(α)cos(β) – sin(α)sin(β) for 0 < α + β < \(\frac{\pi}{2}\)
using the rectangle MNOP in the figure on the right and calculating PM, RN, and RO in terms of α and β.
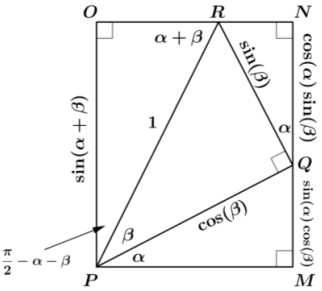
Answer:
PROOF: Let a and fi be real numbers so that 0 < α + β < \(\frac{\pi}{2}\).
Then PM = cos(α) cos(β), RN = sin(α) sin(β), and RO = cos(α + β).
Because RO = PM – RN, it follows that
cos(α + β) = cos(α) cos(β) – sin(α) sin(β) for 0 < α + β < \(\frac{\pi}{2}\).
Question 2.
Derive a formula for tan(2u) for u ≠ \(\frac{\pi}{4}+\frac{k \pi}{2}\) and u ≠ \(\frac{\pi}{2}\) + kπ, for all integers k.
Answer:
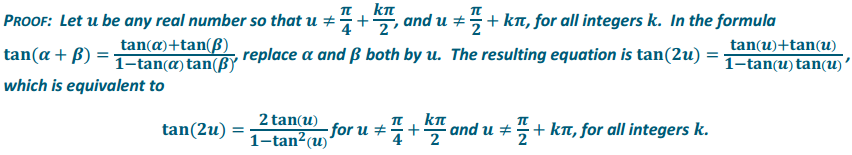
Question 3.
Prove that cos(2u) = 2cos2(u) – 1 for any real number u.
Answer:
PROOF: Let u be any real number. From Exercise 3 in class, we know that cos(2u) = cos2(u) – sin2(u) for any real number u. Using the Pythagorean identity, we know that sin2(u) = 1 – cos2(u). By substitution, cos(2u) = cos2(u) – 1 + cos2(u).
Thus, cos(2u) = 2cos2(u) – 1 for any real number u.
Question 4.
Prove that \(\frac{1}{\cos (x)}\) – cos(x) = sin(x) ∙ tan(x) for x ≠ \(\frac{\pi}{2}\) + kπ, for all integers k.
Answer:
We begin with the left side, get a common denominator, and then use the Pythagorean identity.
PROOF: Let x be a real number so that x ≠ \(\frac{\pi}{2}\) + kπ, for all integers k. Then,
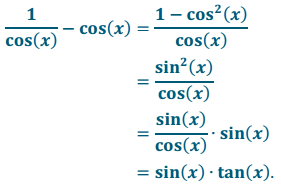
Therefore, \(\frac{1}{\cos (x)}\) – cos(x) = sin(x) ∙ tan(x), where x ≠ \(\frac{\pi}{2}\) + kπ, for all integers k.
Question 5.
Write as a single term: cos (\(\frac{\pi}{4}\) + θ) + cos(\(\frac{\pi}{4}\) – θ).
Answer:
We use the formulas for the cosine of sums and differences:
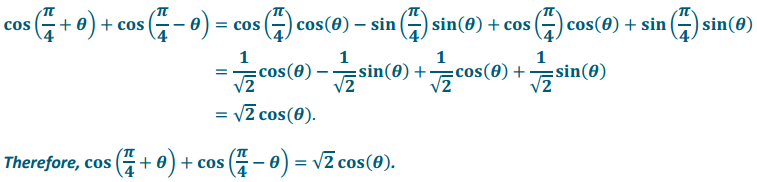
Question 6.
Write as a single term: sin(25°) cos(10°) – cos(25°) sin(10°).
Answer:
Begin with the formula sin(α – β) = sin(α) cos(β) – cos(α) sin(β), and let α = 25° and fi = 10°.
sin(25°) cos(10°) – cos(25°) sin(100) = sin(25° – 10°)
= sin(15°).
Question 7.
Write as a single term: cos(2x) cos(x) + sin(2x) sin(x).
Answer:
Begin with the formula cos(α – β) = cos(α) cos(β) + sin(α) sin(β), and let α = 2x and fi = x.
cos(2x) cos(x) + sin(2x) sin(x) = cos(2x – x)
= cos(x)
Question 8.
Write as a single term: \(\frac{\sin (\alpha+\beta)+\sin (\alpha-\beta)}{\cos (\alpha) \cos (\beta)}\), where cos(α) ≠ 0 and cos(β) ≠ 0.
Answer:
Begin with the formulas for the sine of the sum and difference:
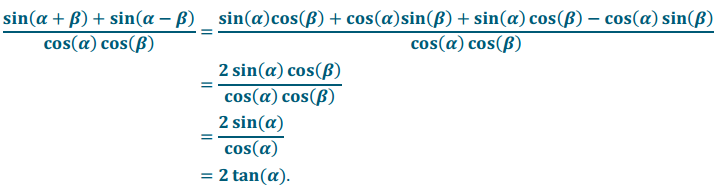
Question 9.
Prove that cos (\(\frac{3 \pi}{2}\) + θ) = sin(θ) for all values of θ.
Answer:
PROOF: Let θ be any real number. Then, from the formula for the cosine of a sum,
cos (\(\frac{3 \pi}{2}\) + θ) = cos \(\left(\frac{3 \pi}{2}\right)\) cos(θ) – sin \(\left(\frac{3 \pi}{2}\right)\) ∙ sin(θ)
= 0 ∙ cos(θ) – (-1) sin(θ)
= sin(θ).
Therefore, cos (\frac{3 \pi}{2} + θ) = sin(θ) for all values of θ.
Question 10.
Prove that cos(π – θ) = – cos(θ) for all values of θ.
Answer:
PROOF: Let π be any real number. Then, from the formula for the cosine of a difference,
cos(π – θ) = cos(π) cos(θ) + sin(π) sin(θ)
= – cos(θ).
Therefore, cos(π – θ) = – cos(θ) for all real numbers θ.
Eureka Math Algebra 2 Module 2 Lesson 17 Exit Ticket Answer Key
Derive a formula for tan(α – β) in terms of tan(α) and tan(β), where α ≠ \(\frac{\pi}{2}\) + kπ and β ≠ \(\frac{\pi}{2}\) + kπ, for all integers k.
Answer: