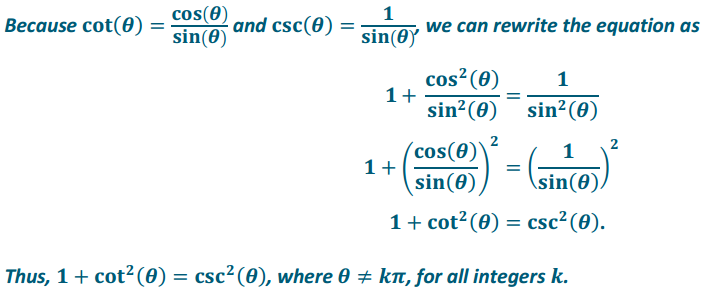Eureka Math Algebra 2 Module 2 Lesson 15 Answer Key

Engage NY Eureka Math Algebra 2 Module 2 Lesson 15 Answer Key

Eureka Math Algebra 2 Module 2 Lesson 15 Exercise Answer Key

Exercise 1.
Recall the Pythagorean identity sin²(θ) + cos²(θ) = 1, where θ is any real number.
a. Find sin(x), given cos(x) = \(\frac{3}{5}\), for \(\frac{\pi}{2}\) < x < 0.
Answer:

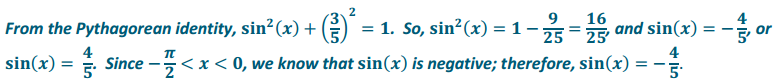
b. Find tan(y), given cos(y) = –\(\frac{5}{13}\) for \(\frac{\pi}{2}\) < y < π.
Answer:

c. Write tan(z) in terms of cos(z), for π < z < \(\frac{3 \pi}{2}\).
Answer:

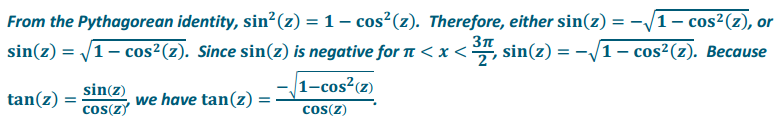
Exercise 2.
Use the Pythagorean identity to do the following:
a. Rewrite the expression cos(θ) sin²(θ) – cos(θ) in terms of a single trigonometric function. State the resulting identity.
Answer:
cos(θ) sin²(θ) – cos(θ) = cos(θ) (sin²(θ) – 1)
= cos(θ) (- cos²(θ))
= – cos³(θ)
Therefore, cos(θ) sin²(θ) – cos(θ) = – cos³(θ) for all real numbers θ.

b. Rewrite the expression (1 – cos²(θ)) csc(θ) in terms of a single trigonometric function. State the resulting identity.
Answer:
(1 – cos²(θ)) csc(θ) = sin²(θ) csc(θ)
= sin²(θ) \(\frac{1}{\sin (\theta)}\)
= sin(θ)
Therefore, (1 – cos²(θ)) csc(θ) = sin(θ) for θ ≠ kπ,for all integers k.

c. Find all solutions to the equation 2 sin²(θ) = 2 + cos(θ) in the interval (θ, 2π). Draw a unit circle that shows the solutions.
Answer:
2 sin²(θ) = 2 + cos(θ)
2(1 – cos²(θ)) = 2 + cos(θ)
2 – 2cos²(θ) = 2 + cos θ
– 2cos²(θ) – cos(θ) = θ
2 cos²(θ) + cos(²) = θ
cos(θ) (2 cos(θ) + 1) = θ
Therefore, cos(θ) = 0, or cos(θ) = –\(\frac{1}{2}\)
See the unit circle on the right, which shows the four points where cos(θ) = 0, or cos(θ) = –\(\frac{1}{2}\).
In the interval (θ, 2π), cos(θ) = 0 only if θ = \(\frac{\pi}{2}\), or
θ = \(\frac{3 \pi}{2}\). Also, cos(θ) = –\(\frac{1}{2}\) only if θ = \(\frac{2 \pi}{3}\), or θ = \(\frac{4 \pi}{3}\) .
Therefore, the solutions of the equations in the interval (0, 2π) are \(\frac{\pi}{2}, \frac{3 \pi}{2}, \frac{2 \pi}{3}\), and \(\frac{4 \pi}{3}\).

Exercise 3.
Which of the following statements are identities? If a statement is an identity, specify the values of x where the equation holds.
a. sin(x + 2π) = sin(x) where the functions on both sides are defined.
Answer:
This is an identity defined for all real numbers.

b. sec(x) = 1 where the functions on both sides are defined.
Answer:
This is not an identity. The functions are not equivalent for all real numbers. For example, although sec(0) = 1, sec\(\left(\frac{\pi}{4}\right)\) = √2. The functions have equal values only when x is an integer multiple of 2π. Additionally, the ranges are different. The range of f(x) = sec(x) is all real numbers y such that y ≤ – 1 or y ≥ 1, whereas the range of g(x) = 1 is the single number 1.

c. sin(-x) = sin(x) where the functions on both sides are defined.
Answer:
This is not an identity; this statement is only true when sin(x) = 0, which happens only at integer multiples of π.

d. 1 + tan²(x) = sec²(x) where the functions on both sides are defined.
Answer:
This is an identity. The functions on either side are defined for θ ≠ \(\frac{\pi}{2}\) + kπ, for all integers k.

e. sin (\(\frac{\pi}{2}\) – x) = cos(x) where the functions on both sides are defined.
Answer:
This is an identity defined for all real numbers.

f. sin²(x) = tan²(x) for all real x.
Answer:
This is not an identity. The equation sin²(x) = tan²(x) is only true where sin²(x) = \(\frac{\sin ^{2}(x)}{\cos ^{2}(x)}\), so cos²(x) = 1, and then cos(x) = 1, or cos(x) = – 1, which gives x = πk, for all integers k. For all other values of x, the functions on the two sides are not equal. Moreover, tan²(x) is defined only for θ ≠ \(\frac{\pi}{2}\) + kπ, for all integers k, whereas sin²(x) is defined for all real numbers.

Another argument for why this statement is not an identity is that sin²\(\left(\frac{\pi}{4}\right)=\left(\frac{\sqrt{2}}{2}\right)^{2}=\frac{1}{2}\) , but tan²\(\left(\frac{\pi}{4}\right)\) = 1² = 1, and 1 ≠ \(\frac{1}{2}\) therefore, the statement is not true for all values of x.

Eureka Math Algebra 2 Module 2 Lesson 15 Problem Set Answer Key

Question 1.
Which of the following statements are trigonometric identities? Graph the functions on each side of the equation.
a. tan(x) = \(\frac{\sin (x)}{\cos (x)}\) where the functions on both sides are defined.
Answer:

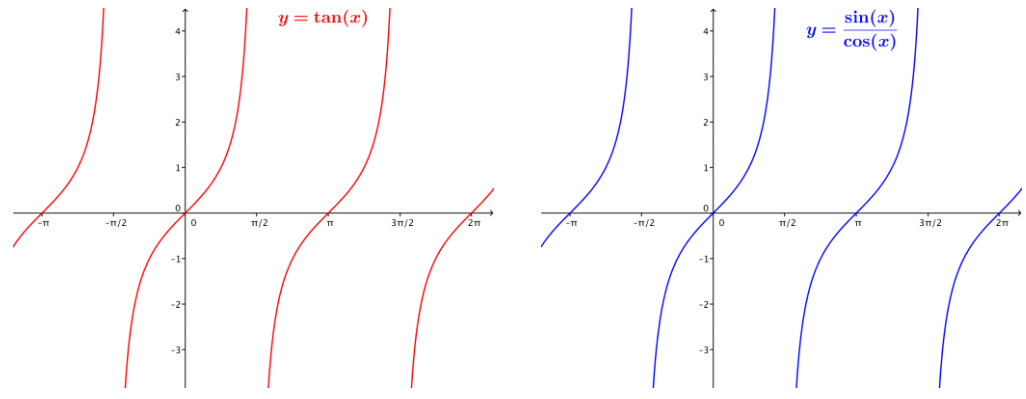
This is an identity that is defined for x ≠ \(\frac{\pi}{2}\) + kπ, for all integers k. See the identical graphs above.

b. cos²(x) = 1 + sin(x) where the functions on both sides are defined.
Answer:
This is not an identity. For example, when x = 0, the left side of the equation is 1, and the right side is also 1.
But when x = \(\frac{\pi}{2}\), the left side is 0, and the right side is 2. The graphs below are clearly different.

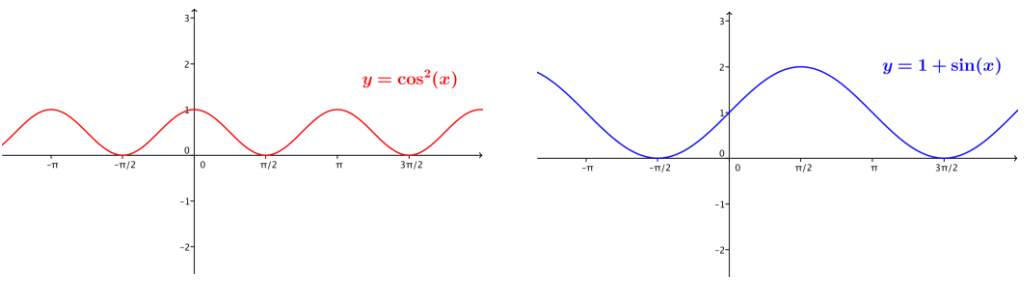
c. cos (\(\frac{\pi}{2}\) – x) = sin(x) where the functions on both sides are defined.
Answer:
This is an identity that is defined for all real numbers x. See the identical graphs below.

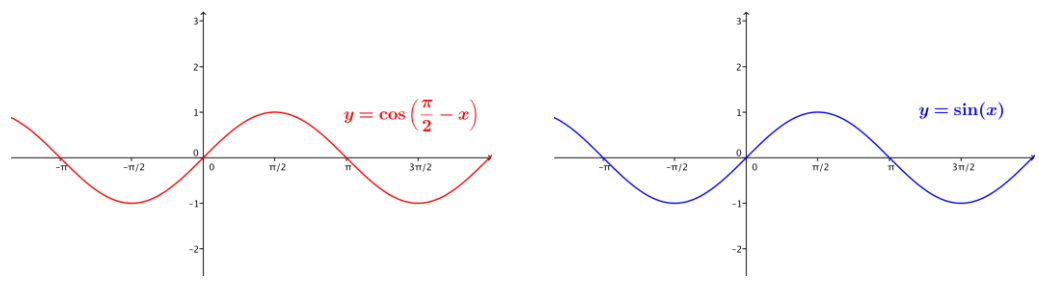
Question 2.
Determine the domain of the following trigonometric identities:
a. cot(x) = \(\frac{\cos (x)}{\sin (x)}\) where the functions on both sides are defined.
Answer:
This identity is defined only for x ≠ kπ, for all integers k.

b. cos(-u) = cos (u) where the functions on both sides are defined.
Answer:
This identity is defined for all real numbers u.

c. sec(y) = \(\frac{1}{\cos (y)}\) where the functions on both sides are defined.
Answer:
This identity is defined for y ≠ \(\frac{\pi}{2}\) + kπ, for all integers k.

Question 3.
Rewrite sin(x)cos²(x) – sin(x) as an expression containing a single term.
Answer:
sin(x) – sin(x)cos²(x) = sin(x)(1 – cos²(x))
= sin(x)sin²(x)
= sin³(x)

Question 4.
Suppose 0 < θ < \(\frac{\pi}{2}\) and sin(θ) = \(\frac{1}{\sqrt{3}}\). What is the value of cos(θ)?
Answer:
cos(θ) = \(\frac{\sqrt{6}}{3}\)

Question 5.
If cos(θ) = –\(\frac{1}{\sqrt{5}}\) what are possible values of sin(θ)?
Answer:
Either sin(θ) = \(\frac{2}{\sqrt{5}}\) or sin(θ) = –\(\frac{2}{\sqrt{5}}\)

Question 6.
Use the Pythagorean identity sin²(θ) + cos²(θ) = 1, where θ is any real number, to find the following:
a. cos(θ), given sin(θ) = \(\frac{5}{13}\), for \(\frac{\pi}{2}\) < θ < π.
Answer:

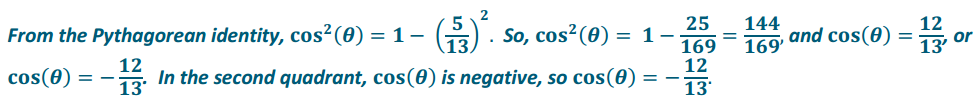
b. tan(x), given cos(x) = –\(\frac{1}{\sqrt{2}}\), for π < x < \(\frac{3 \pi}{2}\).
Answer:

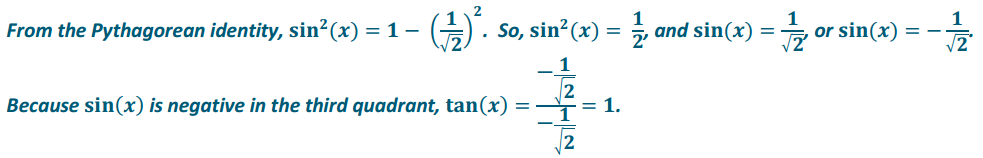
Question 7.
The three identities below are all called Pythagorean identities. The second and third follow from the first, as you saw in Example 1 and the Exit Ticket.
a. For which values of θ are each of these identities defined?
i. sin²(θ) + cos²(θ) = 1, where the functions on both sides are defined.
Answer:
Defined for any real number θ.

ii. tan²(θ) + 1 = sec²(θ), where the functions on both sides are defined.
Answer:
Defined for real numbers θ such that θ ≠ \(\frac{\pi}{2}\) + kπ, for all integers k.

iii. 1 + cot²(θ) = csc²(θ), where the functions on both sides are defined.
Answer:
Defined for real numbers θ such that θ ≠ kπ, for all integers k.

b. For which of the three identities is 0 in the domain of validity?
Answer:
Identities i and ii

c. For which of the three identities is \(\frac{\pi}{2}\) in the domain of validity?
Answer:
Identities i and iii

d. For which of the three identities is –\(\frac{\pi}{4}\) in the domain of validity?
Answer:
Identities i, ii, and iii

Eureka Math Algebra 2 Module 2 Lesson 15 Exit Ticket Answer Key

April claims that 1 + \(\frac{\cos ^{2}(\theta)}{\sin ^{2}(\theta)}\) = \(\frac{1}{\sin ^{2}(\theta)}\) is an identity for all real numbers θ that follows from the Pythagorean identity.

a. For which values of θ are the two functions f(θ) = 1 + \(\frac{\cos ^{2}(\theta)}{\sin ^{2}(\theta)}\) and g(θ) = \(\frac{1}{\sin ^{2}(\theta)}\) defined?
Answer:
Both functions contain sin(θ) in the denominator, so they are undefined if sin(θ) = 0. Thus, the two functions f and g are defined when θ ≠ kπ, for all integers k.

b. Show that the equation 1 + \(\frac{\cos ^{2}(\theta)}{\sin ^{2}(\theta)}\) = \(\frac{1}{\sin ^{2}(\theta)}\) follows from the Pythagorean identity.
Answer:
By the Pythagorean identity, sin²(θ) + cos²(θ) = 1.
If sin(θ) ≠ 0, then,

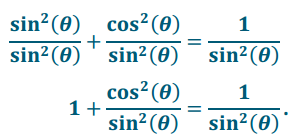
c. Is April correct? Explain why or why not.
Answer:
No. While April’s equation does follow from the Pythagorean identity, it is not valid for all real numbers θ. For example, if θ = π, then both sides of the equation are undefined. In order to divide by sin²(θ), we need to be sure that we are not dividing by zero.

d. Write the equation 1 + \(\frac{\cos ^{2}(\theta)}{\sin ^{2}(\theta)}\) = \(\frac{1}{\sin ^{2}(\theta)}\)in terms of other trigonometric functions, and state the resulting identity.
Answer: