Eureka Math Algebra 2 Module 2 End of Module Assessment Answer Key

Engage NY Eureka Math Algebra 2 Module 2 End of Module Assessment Answer Key

Eureka Math Algebra 2 Module 2 End of Module Assessment Answer Key

Question 1.
a. Graph the function f(x) = 3 cos(2x) + 1 between 0 and 2π.
Answer:
Note that the figure below includes the response to part (b)

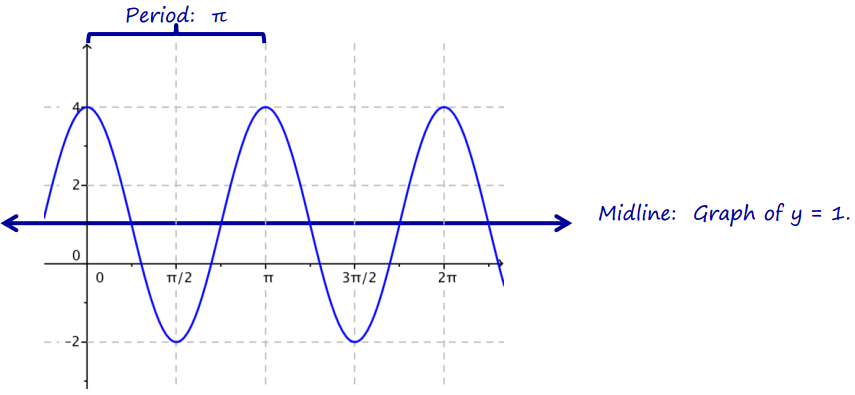
b. Graph and label the midline on your graph. Draw and label a segment to represent the period and specify its length.
Answer:

c. Explain how you can find the midline, period, and amplitude in part (b) from the function f(x) = 3cos(2x) + 1.
Answer:
The midline is y = 1, where 1 is the constant added to the cosine function; the period satisfies the equation
2 = \(\frac{2 \pi}{p}\)

d. Construct a periodic function that has period 8n, a midline given by the equation y = 5, and an amplitude of \(\frac{1}{2}\).
Answer:
A sine or cosine function will work. Using the sine for our solution, we note that for the function in the following form:
f(x) = A sin(ωx) + c.
A is the amplitude, c is the vertical shift, and the period p satisfies \(\frac{2 \pi}{p}\) = ω. So,
f(x) = \(\frac{1}{2}\)sin(\(\frac{1}{4}\)x) + s
will work. Replacing the sine with cosine works equally well.

Question 2.
The graph below shows the number of daylight hours each day of the year in Fairbanks, Alaska, as a function of the day number of the year. (January 1 is day 1, January 2 is day 2, and so on.)

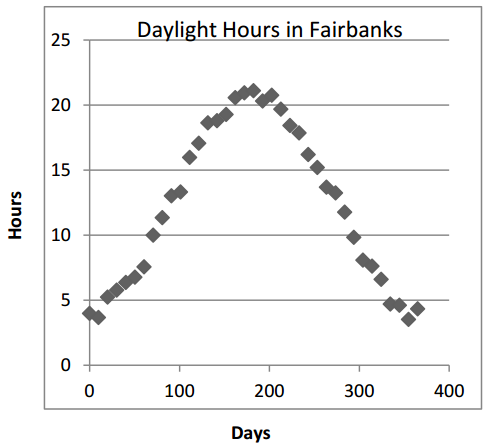
a. Find a function that models the shape of this daylight-hour curve reasonably well. Define the variables you use.
Answer:
Once we have the midline and realize that this is a periodic function, we expect the curve to be a sine or cosine function. It looks like an upside-down cosine graph, so the function will be in the form H(d) = -Acos(ωd) + k, where d is the number of days, k is the height of the midline, A is the distance between the peak (which looks to be about 21) and the midline, and p = \(\frac{2 \pi}{\omega}\) is the period. So, we have

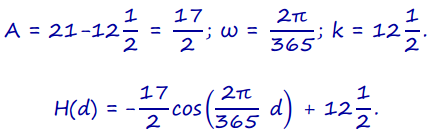
Here, the function H is the number of hours of daylight (in units of hours), and d is the day number as defined at the beginning of the question.
[NOTE: Variations of this formula such as a sine function with a phase shift are possible.]

b. Explain how you chose the numbers in your function from part (a): What is the midline? What is the amplitude? What is the period?
Answer:
The midline is the horizontal line that is halfway between a maximum and minimum value, so it corresponds to the graph of y = 12\(\frac{1}{2}\). The amplitude is described by the distance from a maximum value and the midline, which corresponds to \(\frac{17}{2}\). The period is the horizontal distance between two sequential minimums, which in this problem corresponds to 365.

c. A friend looked at the graph and wondered, “What was the average number of daylight hours in Fairbanks over the past year?” What might be a reasonable answer to that question? Use the structure of the function you created in part (a) to explain your answer.
Answer:
The average number of daylight hours was 12\(\frac{1}{2}\). The average number of daylight hours appears to be given by the midline of the graph of the function, which is given by the value of k in the answer to part (a), that is 12\(\frac{1}{2}\).

d. According to the graph, around which month of the year did the first day of the year with 17.5 hours of daylight occur? Does your function in part (a) agree with your estimation?
Answer:
According to the graph. 17.5 hours of daylight first occurred around day 130. we can check the estimation by substituting it into the function:
H(130) = –\(\frac{17}{2}\)cos(\(\frac{2 \pi}{365}\) ∙ 130) + 12\(\frac{1}{2}\) = 17.8
The value of H(130) is 17.8 hours of light, which is pretty close to the number of daylight hours estimated from the graph.
Note: An exact answer is not needed here. Likely reasonable answers include: 120, 125, 130, 133, or anything in between.

e. The scientists who reported these data now inform us that their instruments were incorrectly calibrated; each measurement of the daylight hours is 15 minutes too long. Adjust your function from part (a) to account for this change in the data. How does your function now appear? Explain why you changed the formula as you did.
Answer:
To correct the measurement, you need to take away \(\frac{1}{4}\) hours of daylight from each measurement so that it lowers the midline by \(\frac{1}{4}\) hours: H(d) = –\(\frac{17}{2}\) cos(\(\)d) + 12\(\frac{1}{4}\).

f. To make very long-term predictions, researchers would like a function that acknowledges that there are, on average, 365\(\frac{1}{4}\) days in a year. How should you adjust your function from part (e) so that it represents a function that models daylight hours with a period of 365\(\frac{1}{4}\) days? How does your function now appear?
Answer:

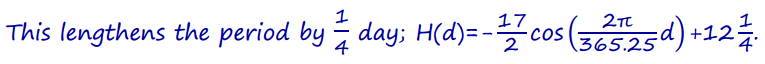
g. Do these two adjustments to the function significantly change the prediction as to which day of the year first possesses 17.5 hours of daylight?
Answer:
Using the new function and repeating the calculations as in part (d), we have

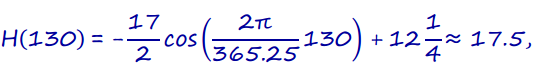
Which is not a great change between the two predictions (the difference is less than 0.3 hours), but the function definitely seems to be more accurate with this additional information.

Question 3.
On a whim, James challenged his friend Susan to model the movement of a chewed-up piece of gum stuck to the rim of a rolling wheel with radius 1 m. To simplify the situation, Susan drew a diagram of a circle to represent the wheel and imagined the gum as a point on the circle. Furthermore, she assumed that the center of the wheel was moving to the right at a constant speed of 1 m/sec, as shown in the diagram.

At time t = 0 seconds, the piece of gum was directly left of the center of the wheel, as indicated in the diagram above.
a. What is the first time that the gum was at the top position of the wheel?
Answer:
Since the wheel was rolling at 1 meter per second, it made a complete turn after 2π seconds, rotating clockwise at a constant rate of 1 radian per second. Hence, the top position was reached after the gum has rotated \(\frac{\pi}{2}\) radians, which occurs at time \(\frac{\pi}{2}\) seconds.

b. What is the first time that the gum was again directly to the left of the center of the wheel?
Answer:
The gum did one complete turn, which occurred after the gum had rotated 2π radians, which is at time 2π seconds.

c. After doing some initial calculations as in parts (a) and (b), Susan realized that the height of the gum is a function of time. She let V(t) stand for the vertical height of the gum from the ground at time t seconds. Find a formula for her function.
Answer:
V(t) = 1 + sin (π – t) or V(t) = 1 + sin(t).

d. What is the smallest positive value of t for which V(t) = 0? What does this value of t represent in terms of the situation?
Answer:
We want the first positive number that satisfies 1 + sin(t) = 0. This occurs when t = \(\frac{\pi}{2}\). At \(\frac{\pi}{2}\) seconds, the gum will be on the ground.

Next, Susan imagined that the wheel was rolling along the horizontal axis of a coordinate system, with distances along the horizontal axis given in units of meters (and height along the vertical axis also given in units of meter). At time t = 0, the center of the wheel has coordinates (1, 1) so that the gum was initially at position (0, 1).

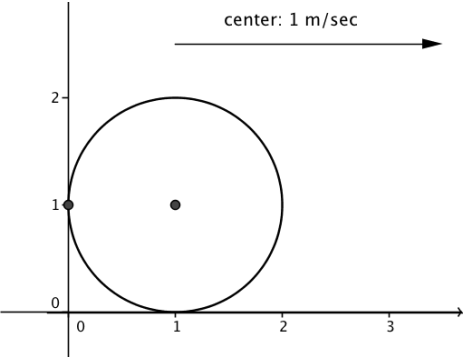
e. What is the x-coordinate of the position of the gum after \(\frac{\pi}{2}\) seconds (when it first arrived at the top of the wheel)? After ir seconds (when it was directly to the right of the center)?
Answer:
The wheel has moved forward \(\frac{\pi}{2}\) meters, and the point, with the respect to the wheel, has moved one unit to the right. It x-coordinate is thus 1 + \(\frac{\pi}{2}\) meters. similarly, after π seconds, the x – coordinate of the gum was (1 + π) + 1 meters away from the starting position, which was 2 + π meters.

f. From the calculations like those in part (e), Susan realized that the horizontal distance, H, of the gum from its initial location is also a function of time t, given by the distance the wheel traveled plus its horizontal displacement from the center of the wheel. Write a formula H(t) for the function (i.e., find a function that specifies the x-coordinate of the position of the gum at time t).
Answer:
After t seconds, the center of the wheel is at position 1 + t meters. we add this distance to the horizontal displacement that the gum is away from the center (the gum is horizontally moving back and forth with respect to the center). The horizontal displacement can be modeled by -cos(t) (or equivalently, cos(π – t)). Adding the two terms together specifies the x-coordinate of the gum at time t:
H(t) = 1 + t + cos(π – t), or H(t) = 1 + t – cos(t).

g. Susan and James decide to test Susan’s model by actually rolling a wheel with radius 1 m. However, when the gum first touched the ground, it came off the wheel and stuck to the ground at that position. How horizontally far from the initial position is the gum? Verify that your function from part (f) predicts this answer, too.
Answer:
The gum is on the ground at time \(\frac{3 \pi}{2}\) seconds, and the wheel has rolled \(\frac{3 \pi}{2}\) meters during this time. The center of the wheel is at x-coordinate 1 + \(\frac{3 \pi}{2}\) meters, which is also the x-coordinate of the gum (which is directly below the center at this time).
Using the formula H(t) = 1 + t – cos(t) from part (f) gives
H\(\left(\frac{3 \pi}{2}\right)\) = 1 + \(\frac{3 \pi}{2}\) – cos\(\left(\frac{3 \pi}{2}\right)\) = 1 + \(\frac{3 \pi}{2}\) + 0. These agree.

Question 4.
Betty was looking at the Pythagorean Identity: for all real numbers θ,
sin²(θ) + cos²(θ) = 1.
a. Betty used the Pythagorean identity to make up the equation below. She then stated, “Wow, I’ve discovered a new identity that is true for all θ.” Do you agree with her? Why or why not?
\(\frac{\sin ^{2}(\theta)}{1-\cos (\theta)}\) = 1 + cos(θ)
Answer:
This is not an identity for all values of θ because the expressions on each side of the equation, thought of as functions, have different domains. The domain of the function on the left excludes 0 (and other places where the cosine is 1), whereas the one on the right does not.

b. Prove the Pythagorean identity.
Answer:
For any real number θ, rotate the initial ray (given by the positive x-axis) by θ radians The image of the intial ray under that rotation intersects the unit circle at that point (x, y). By definition, cos(θ) = x and sin(θ) = y. However, the point (x, y) is also a point on the unit circle, so it satisfies the equation x² + y² = 1. Substituting cos(θ) for x and sin(θ) for y into this equation yields the desired identity.

c. The real number θ is such that sin(θ) = 0.6. Calculate |cos(θ)| and |tan(θ)|.
Answer:
sin²(θ) + cos²(θ) = 1
0.36 + cos²(θ) = 1
cos²(θ) = 0.64
|cos(θ)| = 0.8
|tan(θ)| = \(\frac{0.6}{0.8}\) = 0.75

d. Suppose additional information is given about the number θ from part (c). You are told that \(\frac{\pi}{2}\) < θ < π. What are the values of cos(θ) and tan(θ)? Explain.
Answer:
The cosine and tangent are negative for rotations that place the terminal ray in the second quadrant. so, the cosine and tangent are cos(θ) = -0.8 and tan(θ) = – 0.75.