Eureka Math Algebra 2 Module 1 Lesson 6 Answer Key

Engage NY Eureka Math Algebra 2 Module 1 Lesson 6 Answer Key

Eureka Math Algebra 2 Module 1 Lesson 6 Example Answer Key

Example 1.
What is the quotient of \(\frac{x^{2}-a^{2}}{x-a}\)? Use the reverse tabular method or long division.
Answer:

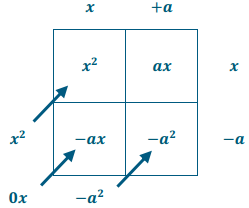
The result of dividing x² – a² by x – a is x + a.

Eureka Math Algebra 2 Module 1 Lesson 6 Opening Exercise Answer Key

Exercise 1.
Find the following quotients, and write the quotient in standard form.
a. \(\frac{x^{2}-9}{x-3}\)
Answer:
x + 3

b. \(\frac{x^{3}-27}{x-3}\)
Answer:
x² + 3x + 9

c. \(\frac{x^{4}-81}{x-3}\)
Answer:
x³ + 3x² + 9x + 27

Eureka Math Algebra 2 Module 1 Lesson 6 Exercise Answer Key

Exercise 1.
Use patterns to predict each quotient. Explain how you arrived at your prediction, and then test it by applying the reverse tabular method or long division.
a. \(\frac{x^{2}-144}{x-12}\)
Answer:
The quotient is x + 12. I arrived at this conclusion by noting that 144 = 12², so I could apply the patterns in the previous problems to obtain the result.

b. \(\frac{x^{3}-8}{x-2}\)
Answer:
The quotient is x² + 5x + 25. The dividend is the difference of two perfect cubes, x³ and 2³ = 8. Based on the patterns in the Opening Exercise, the quotient will be a quadratic polynomial with coefficients that are ascending powers of 2 starting with 2⁰.

c. \(\frac{x^{3}-125}{x-5}\)
Answer:
The quotient is x² + 5x + 25. As in part (b), the numerator is a difference of cubes, x³ and 5³ = 125. Based on the patterns in the Opening Exercise, the quotient will be a quadratic polynomial with coefficients that are ascending powers of 5 starting with 5⁰.

d. \(\frac{x^{6}-1}{x-1}\)
Answer:
The dividend is the difference of two values raised to the 6^th power, 1⁶ = 1 and x⁶. Extending the patterns we’ve seen in the Opening Exercise and the previous exercises, the quotient should be a 5^th degree polynomial with coefficients that are ascending powers of 1, so all coefficients will be 1. Thus, the quotient is x⁵ + x⁴ + x³ + x² + x + 1.

Exercise 2.
Work with your group to find the following quotients.
a. \(\frac{x^{3}-a^{3}}{x-a}\)
Answer:
x² + ax + a²

b. \(\frac{x^{4}-a^{4}}{x-a}\)
Answer:
x³ + ax² + a²x + a³

Before moving on, discuss these results as a whole class. It may be necessary to model a solution to the third question below if students are still struggling with connecting division back to multiplication.
→ What patterns do you notice in the quotient?
→ The terms are always added, and each term is a product of a power of and a power of a as the powers of decrease by 1 for each consecutive term, the powers of increase by 1.
→ How do these patterns compare to the ones you observed in the opening exercises?
→ They support the patterns we discovered earlier. This work shows that we can quickly compute the quotient for any problem that fits the pattern.
→ How can you rewrite these division problems as multiplication problems?
→ The dividend is equal to the product of the quotient and the divisor. For example,
x³ – a³ = (x – a) (x² + ax + a²) The other problems would be x² – a² = (x – a) (x + a) and x⁴ – a⁴ = (x – a) (x³ + ax² + a²x + a³).

Exercise 3.
Predict without performing division whether or not the divisor will divide into the dividend without a remainder for the following problems. If so, find the quotient. Then check your answer.
a. \(\frac{x^{2}-a^{2}}{x+a}\)
Answer:
The quotient is x – a This makes sense because we already showed that the result when dividing by x – a is x + a.

b. \(\frac{x^{3}-a^{3}}{x+a}\)
Answer:
This problem does not divide without a remainder; therefore, x + a is not a factor of x³ – a³.

c. \(\frac{x^{2}+a^{2}}{x+a}\)
Answer:
This problem does not divide without a remainder; therefore, x + a is not a factor of x² + a²

d. \(\frac{x^{3}+a^{3}}{x+a}\)
Answer:
The quotient is x² – ax + a². This result is similar to our work in Exercise 2 except the middle term is – ax instead of ax.

Exercise 4.
a. Find the quotient \(\frac{x^{n}-1}{x-1}\) for n = 2, 3, 4, and 8.
Answer:
For n = 2, the quotient is x + 1
For n = 3, the quotient is x² + x + 1.
For n = 4, the quotient is x³ + x² + x + 1
For n = 8, the quotient is x⁷ + x⁶ + x⁵ + ……. + x + 1.

b. What patterns do you notice?
Answer:
The degree of the quotient is less than the degree of the dividend. The degree of each term is less than the degree of the previous term. The last term is 1. The number of terms will be equal to the degree of the dividend.

c. Use your work in part (a) to write an expression equivalent to \(\frac{x^{n}-1}{x-1}\) for any integer n > 1.
Answer:
x^n-1 + x^n-2 + x^n-3 + …… + x¹ + 1

Eureka Math Algebra 2 Module 1 Lesson 6 Problem Set Answer Key

Question 1.
Compute each quotient.
a. \(\frac{x^{2}-625}{x-25}\)
Answer:
x + 25

b. \(\frac{x^{3}+1}{x+1}\)
Answer:
x² – x + 1

c. \(\frac{x^{3}-\frac{1}{8}}{x-\frac{1}{2}}\)
Answer:
x² + \(\frac{1}{2}\)x + \(\frac{1}{4}\)

d. \(\frac{x^{2}-0.01}{x-0.1}\)
Answer:
x + 0.1

Question 2.
In the next exercises, you can use the same identities you applied in the previous problem. Fill in the blanks in the problems below to help you get started. Check your work by using the reverse tabular method or long division to make sure you are applying the identities correctly.
a.

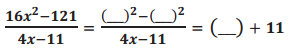
Answer:
4x, 11, 4x

b.

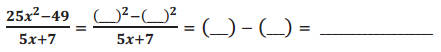
Answer:
5x, 7, 5x, 7, 5x – 7

c.

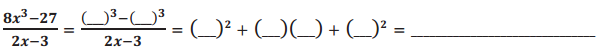
Answer:
2x, 3, 2x, 2x, 3, 3, 4x² + 6x + 9

Question 3.
Show how the patterns and relationships learned in this lesson could be applied to solve the following arithmetic problems by filling in the blanks.
a.

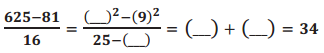
Answer:
\(\frac{25^{2}-9^{2}}{25-9}\) = 25 + 9 = 34

b.

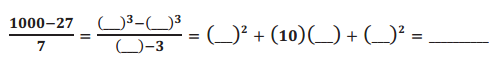
Answer:
\(\frac{10^{3}-3^{3}}{10-3}\) = 10² + 10(3) + 3² = 139

c.

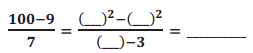
Answer:
\(\frac{10^{2}-3^{2}}{10-3}\) = 10 + 3 = 13

d.

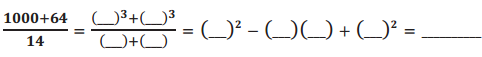
Answer:
\(\frac{10^{3}+4^{3}}{10+4}\) = 10² – 10(4) + 4² = 76

Question 4.
Apply the identities from this lesson to compute each quotient. Check your work using the reverse tabular method or long division.
a. \(\frac{16 x^{2}-9}{4 x+3}\)
Answer:
4x – 3

b. \(\frac{81 x^{2}-25}{18 x-10}\)
Answer:
\(\frac{9}{2} x+\frac{5}{2}\)

c. \(\frac{27 x^{3}-8}{3 x-2}\)
Answer:
9x² + 6x + 4

Question 5.
Extend the patterns and relationships you learned in this lesson to compute the following quotients. Explain your reasoning, and then check your answer by using long division or the tabular method.
a. \(\frac{8+x^{3}}{2+x}\)
Answer:
The quotient is 4 – 2x + x². This problem has the variable and constant terms reversed using the commutative property, so it is the same as computing (x³ + 8) ÷ (x + 2).

b. \(\frac{x^{4}-y^{4}}{x-y}\)
Answer:
The quotient is x³ + x²y + xy² + y³ This problem is similar to Opening Exercise part (c), except that instead of 81 and 3 in the dividend and quotient, we have a power of y. You can also extend the patterns for
\(\frac{x^{3}-a^{3}}{x-a}\) = x² + ax² + a² using the variable instead of the variable

c. \(\frac{27 x^{3}+8 y^{3}}{3 x+2 y}\)
Answer:
The quotient is 9x² – 6xy + 4y². In this example, 3x is in the x position, and 2y is in the a position. Then, the divisor fits the pattern of x³ + a³

d. \(\frac{x^{7}-y^{7}}{x-y}\)
Answer:
The quotient is x⁶ + x⁵y + x⁴y² + x³y³ + x²y⁴ + xy⁵ + y⁶. In this problem, replace 1 with y and extend the powers of y pattern using the identities in the Lesson Summary.

Eureka Math Algebra 2 Module 1 Lesson 6 Exit Ticket Answer Key

Compute each quotient using the identities you discovered in this lesson.

Question 1.
\(\frac{x^{4}-16}{x-2}\)
Answer:
\(\frac{x^{4}-16}{x-2}\) = x³ + 2x² + 4x + 8

Question 2.
\(\frac{x^{3}+1000}{x+10}\)
Answer:
\(\frac{x^{3}+1000}{x+10}\) = x² – 10x + 100

Question 3.
\(\frac{x^{5}-1}{x-1}\)
Answer:
\(\frac{x^{5}-1}{x-1}\) = x⁴ + x³ + x² + x + 1