Engage NY Eureka Math Algebra 2 Module 1 Lesson 5 Answer Key
Eureka Math Algebra 2 Module 1 Lesson 5 Exercise Answer Key
Exercises 1 – 15: Polynomial Pass
Perform the indicated operation to write each polynomial in standard form.
Exercise 1.
(x – 3) (x2 + 3x – 1)
Answer:
x4 + 3x3 – 4x2 – 9x + 3
Exercise 2.
(5x2 – 3x – 7) – (x2 + 2x – 5)
Answer:
4x2 – 5x – 2
Exercise 3.
\(\frac{x^{3}-8}{x-2}\)
Answer:
x2 + 2x + 4
Exercise 4.
(x + 1) (x – 2) (x + 3)
Answer:
x3 + 2x2 – 5x – 6
Exercise 5.
(x + 1) – (x – 2) – (x + 3)
Answer:
– x
Exercise 6.
(x + 2) (2x2 – 5x + 7)
Answer:
2x3 – x2 – 3x + 14
Exercise 7.
\(\frac{x^{3}-2 x^{2}-65 x+18}{x-9}\)
Answer:
x2 + 7x – 2
Exercise 8.
(x2 – 3x + 2) – (2 – x + 2x2)
Answer:
– x2 – 2x
Exercise 9.
(x2 – 3x + 2) (2 – x + 2x2)
Answer:
2x4 – 7x3 + 9x2 – 8x + 4
Exercise 10.
\(\frac{x^{3}-x^{2}-5 x-3}{x-3}\)
Answer:
x2 + 2x + 1
Exercise 11.
(x2 + 7x – 12) (x2 – 9x + 1)
Answer:
x4 – 2x3 – 74x2 + 115x – 12
Exercise 12.
(2x3 – 6x2 – 7x – 2) + (x3 + x2 + 6x – 12)
Answer:
3x3 – 5x2 – x – 14
Exercise 13.
(x3 – 8) (x2 – 4x + 4)
Answer:
x5 – 4x4 + 4x3 – 8x2 + 32x – 32
Exercise 14.
\(\frac{x^{3}-2 x^{2}-5 x+6}{x+2}\)
Answer:
x2 – 4x + 3
Exercise 15.
(x3 + 2x2 – 3x – 1) + (4 – x – x3)
Answer:
2x2 – 4x + 3
Exercise 16.
Review Exercises 1 – 15 and then select one exercise for each category and record the steps in the operation below as an example. Be sure to show all your work.
Answer:
Exercises 17 – 20
For Exercises 17 – 20, rewrite each polynomial in standard form by applying the operations in the appropriate order.
Exercise 17.
\(\frac{\left(x^{2}+5 x+20\right)+\left(x^{2}+6 x-6\right)}{x+2}\)
Answer:
2x + 7
Exercise 18.
(x2 – 4) (x + 3) – (x2 + 2x – 5)
Answer:
x3 + 2x2 – 6x – 7
Exercise 19.
\(\frac{(x-3)^{3}}{x^{2}-6 x+9}\)
Answer:
x – 3
Exercise 20.
(x + 7) (2x – 3) – (x3 – 2x2 + x – 2) ÷ (x – 2)
Answer:
x2 + 11x – 22
Exercise 21.
What would be the first and last terms of the polynomial if it was rewritten in standard form? Answer these quickly without performing all of the indicated operations.
a. (2x3 – x2 – 9x + 7) + (11x2 – 6x3 + 2x – 9)
Answer:
First term: – 4x3 Last term: – 2
b. (x – 3) (2x + 3) (x – 1)
Answer:
First term: 2x3, Last term: – 18
c. (2x – 3) (3x + 5) – (x + 1) (2x2 – 6x + 3)
Answer:
First term: – 2x3, Last term: – 18
d. (x + 5) (3x – 1) – (x – 4)2
Answer:
First term: 2x2, Last term: – 21
Exercise 22.
What would the first and last terms of the polynomial be if it was rewritten in standard form?
a. (n + 1) (n + 2) (n + 3) : (n + 9) (n + 10)
Answer:
First term: n10, Last term: 10!
b. (x – 2)10
Answer:
First term: x10, Last term: (- 2)10
c. \(\frac{(x-2)^{10}}{(x-2)}\)
Answer:
First term: x9, Last term: (-2)9
d. \(\frac{n(n+1)(2 n+1)}{6}\)
Answer:
First term: \(\frac{1}{3}\)n3,
Last term: \(\frac{n}{6}\)
Eureka Math Algebra 2 Module 1 Lesson 5 Problem Set Answer Key
For Problems 1 – 7, rewrite each expression as a polynomial in standard form.
Question 1.
(3x – 4)3
Answer:
27x3 – 108x2 + 144x – 64
Question 2.
(2x2 – x3 – 9x + 1) – (x3 + 7x – 3x2 + 1)
Answer:
– 2x3 + 5x2 – 16x
Question 3.
(x2 – 5x + 2) (x – 3)
Answer:
x3 – 8x2 + 17x – 6
Question 4.
\(\frac{x^{4}-x^{3}-6 x^{2}-9 x+27}{x-3}\)
Answer:
x3 + 2x2 – 9
Question 5.
(x + 3) (x – 3) – (x + 4) (x – 4)
Answer:
7
Question 6.
(x + 3) (x – 3) – (x + 4) (x – 4)
Answer:
7
Question 7.
\(\frac{x^{2}-5 x+6}{x-3}+\frac{x^{3}-1}{x-1}\)
Answer:
x2 + 2x – 1
For Problems 8 – 9: Quick, what would be the first and last terms of the polynomial if it was written in standard form?
Question 8.
2(x2 – 5x + 4) – (x + 3) (x + 2)
Answer:
The first and last term are x2 and 2.
Question 9.
\(\frac{(x-2)^{5}}{x-2}\)
Answer:
The first and last terms are x4 and 16.
Question 10.
The profit a business earns by selling x items is given by the polynomial function
p(x) = x(160 – x) – (100x + 500).
What is the last term in the standard form of this polynomial? What does it mean in this situation?
Answer:
The last term is – 500 so that p(0) = – 500. This means that if no items are sold, the company would lose $500.
Question 11.
Explain why these two quotients are different. Compute each one. What do they have in common? Why?
\(\frac{(x-2)^{4}}{x-2}\) and \(\frac{x^{4}-16}{x-2}\)
Answer:
The quotients are x3 – 6x2 + 12x – 8 and x3 + 2x2 + 4x + 8.
They are different because the dividends are not equivalent expressions. The quotients have the first and last terms in common because division is going to reduce the degree by the difference of the degrees of the numerator and denominator, and their leading coefficients were both one. When multiplying, the last term of a polynomial in standard form is the product of the lowest degree terms in each factor. Therefore, when dividing, the last term of the quotient will be the quotient of the last term of the dividend and divisor.
Question 12.
What are the area and perimeter of the figure? Assume there is a right angle at each vertex.
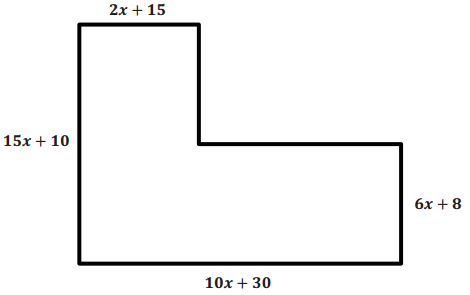
Answer:
The missing horizontal side length is 8x + 15. The missing vertical side length is 9x + 2. I determined these lengths by subtracting the vertical lengths and by subtracting the horizontal lengths. The perimeter is 50x + 80. I got this by adding the lengths of all of the sides together. The area can be found by splitting the shape either horizontally or vertically into two rectangles. If split vertically, the areas of the rectangles are (15x + 10) (2x + 15) and (6x + 8) (8x + 15). The total area of the figure is the sum of these two products, 78x2 + 399x + 270.
Eureka Math Algebra 2 Module 1 Lesson 5 Exit Ticket Answer Key
Question 1.
Jenny thinks that the expression below is equal to x2 – 4. If you agree, show that she is correct. If you disagree, show that she is wrong by rewriting this expression as a polynomial in standard form. \(\frac{(x-2)^{3}}{x-2}\)
Answer:
Multiple approaches are possible to justify why Jenny is incorrect. One possible solution is shown below.
Jenny is incorrect. To perform this operation, you can first divide by x – 2 and then expand the quotient.
\(\frac{(x-2)^{3}}{x-2}\) = (x – 2)2
= x2 – 4x + 4