Engage NY Eureka Math Algebra 2 Module 1 Lesson 28 Answer Key
Eureka Math Algebra 2 Module 1 Lesson 28 Example Answer Key
Example 1.
Solve the following radical equation. Be sure to check your solutions.
\(\sqrt{3 x+5}\) – 2 = – 1
Answer:
\(\sqrt{3 x+5}\) = 1
3x + 5 = 1
3x = – 4
x = –\(\frac{4}{3}\)
Check: \(\sqrt{3\left(-\frac{4}{3}\right)+5}\) – 2 = \(\sqrt{-4+5}\) – 2 = \(\sqrt{1}\) – 2 = – 1, so – \(\frac{4}{3}\) is a valid solution.
Example 2.
Rationalize the denominator in each expression. That is, rewrite the expression so that there is a rational expression in the denominator.
a. \(\frac{x-9}{\sqrt{x-9}}\)
Answer:
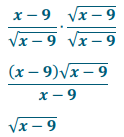
b. \(\frac{x-9}{\sqrt{x}+3}\)
Answer:
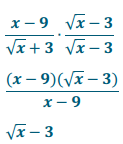
Eureka Math Algebra 2 Module 1 Lesson 28 Exercise Answer Key
For Exercises 1 – 4, describe each step taken to solve the equation. Then, check the solution to see if it is valid. If it is not a valid solution, explain why.
Exercise 1.
√x – 6 = 4
Answer:
√x = 10 Add 6 to both sides.
x = 100 Square both sides.
Check √100 – 6 = 10 – 6 = 4
So 100 is a valid a solution .
Exercise 2.
\(\sqrt[3]{x}\) – 6 = 4
Answer:
\(\sqrt[3]{x}\) = 10 Add 6 to both sides.
x = 1000 Cube both sides.
Check: \(\sqrt[3]{1000}\) – 6 = 10 – 6 = 4
So 1,000 is a valid solution.
Exercise 3.
√x + 6 = 4
Answer:
√x = – 2
x = 4
Check: √4 + 6 = 2 + 6 = 8, and 8 ≠ 4, s0 4 is not a valid solution.
Exercise 4.
\(\sqrt[3]{x}\) + 6 = 4
Answer:
\(\sqrt[3]{x}\) = – 2
x = – 8
Check: \(\sqrt[3]{-8}\) + 6 = – 2 + 6 = 4, so, – 8 is a valid solution.
Exercises 5 – 15
Solve each radical equation. Be sure to check your solutions.
Exercise 5.
\(\sqrt{2 x-3}\) = 11
Answer:
62
Exercise 6.
\(\sqrt[3]{6-x}\) = – 3
Answer:
33
Exercise 7.
\(\sqrt{x+5}\) – 9 = – 12
Answer:
No solution
Exercise 8.
\(\sqrt{4 x-7}\) = \(\sqrt{3 x+9}\)
Answer:
16
Exercise 9.
-12\(\sqrt{x-6}\) = 18
Answer:
No solution
Exercise 10.
\(3 \sqrt[3]{x+2}\) = 12
Answer:
62
Exercise 11.
\(\sqrt{x^{2}-5}\) = 2
Answer:
3, – 3
Exercise 12.
\(\sqrt{x^{2}+8 x}\) = 3
Answer:
– 9, 1
Compute each product, and combine like terms.
Exercise 13.
(√x + 2) (√x – 2)
Answer:
x – 4
Exercise 14.
(√x + 4) (√x + 4)
Answer:
x + 8√x + 16
Exercise 15.
\((\sqrt{x-5})(\sqrt{x-5})\)
Answer:
x – 5
Exercises 16 – 18
Exercise 16.
Rewrite \(\frac{1}{\sqrt{x}-5}\) in an equivalent form with a rational expression in the denominator.
Answer:
\(\frac{\sqrt{x}+5}{x-25}\)
Exercise 17.
Solve the radical equation \(\frac{3}{\sqrt{x+3}}\) = 1. Be sure to check for extraneous solutions.
Answer:
x = 6
Exercise 18.
Without solving the radical equation \(\sqrt{x+5}\) + 9 = 0, how could you tell that it has no real solution?
Answer:
The value of the radical expression \(\sqrt{x+5}\) must be positive or zero. In either case, adding 9 to it cannot give zero.
Eureka Math Algebra 2 Module 1 Lesson 28 Problem Set Answer Key
Question 1.
a. If √x = 9, then what is the value of x?
Answer:
x = 81
b. If x2 = 9, then what is the value of x?
Answer:
x = 3 or x = – 3
c. Is there a value of x such that \(\sqrt{x+5}\) = 0? If yes, what is the value? If no, explain why not.
Answer:
Yes, x = – 5
d. Is there a value of x such that √x + 5 = 0? If yes, what is the value? If no, explain why not.
Answer:
No, √x will be a positive value or zero for any value of x, so the sum cannot equal 0. If x = 25, then
√25 + 5 = 10.
Question 2.
a. Is the statement \(\sqrt{x^{2}}\) = x true for all x-values? Explain.
Answer:
No, this statement is only true for x ≥ 0. If x < 0, it is not true. For example, if x = – 5, \(\sqrt{(-5)^{2}}\) = √25 = 5, then \(\sqrt{(-5)^{2}}[latex] ≠ – 5.
b. Is the statement [latex]\sqrt[3]{x^{3}}\) = x true for all x-values? Explain.
Answer:
Yes, this statement is true for all x-values. For example, if x = 2, then \(\sqrt[3]{2^{3}}\) = 2. If x = – 2, then \(\sqrt[3]{(-2)^{3}}\) = – 2. Since the cube root of a positive number is positive, and the cube root oía negative number is negative, this statement is true for any value of x.
Rationalize the denominator in each expression.
Question 3.
\(\frac{4-x}{2+\sqrt{x}}\)
Answer:
2 – √x
Question 4.
\(\frac{2}{\sqrt{x-12}}\)
Answer:
\(\frac{2 \sqrt{x-12}}{x-12}\)
Question 5.
\(\frac{1}{\sqrt{x+3}-\sqrt{x}}\)
Answer:
\(\frac{\sqrt{x+3}+\sqrt{x}}{3}\)
Solve each equation, and check the solutions.
Question 6.
\(\sqrt{x+6}\) = 3
Answer:
x = 3
Question 7.
2\(\sqrt{x+3}\) = 6
Answer:
x = 6
Question 8.
\(\sqrt{x+3}\) + 6 = 3
Answer:
No solution
Question 9.
\(\sqrt{x+3}\) – 6 = 3
Answer:
x = 78
Question 10.
16 = 8 + √x
Answer:
x = 64
Question 11.
\(\sqrt{3 x-5}\) = 7
Answer:
x = 18
Question 12.
\(\sqrt{2 x-3}\) = \(\sqrt{10-x}\)
Answer:
x = \(\frac{13}{3}\)
Question 13.
3\(\sqrt{x+2}\) + \(\sqrt{x-4}\) = 0
Answer:
No solution
Question 14.
\(\frac{\sqrt{x+9}}{4}\) = 3
Answer:
x = 135
Question 15.
\(\frac{12}{\sqrt{x+9}}\) = 3
Answer:
x = 7
Question 16.
\(\sqrt{x^{2}+9}\) = 5
Answer:
x = 4 or x = – 4
Question 17.
\(\sqrt{x^{2}-6 x}\) = 4
Answer:
x = 8 or x = – 2
Question 18.
\(\frac{5}{\sqrt{x-2}}\) = 5
Answer:
x = – 1
Question 19.
\(\frac{5}{\sqrt{x}-2}\) = 5
Answer:
x = 9
Question 20.
\(\sqrt[3]{5 x-3}\) + 8 = 6
Answer:
x = – 1
Question 21.
\(\sqrt[3]{9-x}\) = 6
Answer:
x = – 207
Question 22.
Consider the inequality \(\sqrt{x^{2}+4 x}\) > 0. Determine whether each x-value is a solution to the inequality.
a. x = – 10
Answer:
Yes
b. x = – 4
Answer:
No
c. x = 10
Answer:
Yes
d. x = 4
Answer:
Yes
Question 23.
Show that \(\frac{a-b}{\sqrt{a}-\sqrt{b}}\) = \(\sqrt{a}+\sqrt{b}\) for all values of a and b such that a > 0 and b > 0 and a B b.
Answer:
If we multiply the numerator and denominator of \(\frac{a-b}{\sqrt{a}-\sqrt{b}}\) by \(\sqrt{a}+\sqrt{b}\) to rationalize the denominator, then we have
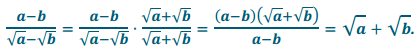
Question 24.
Without actually solving the equation, explain why the equation \(\sqrt{x+1}\) + 2 = 0 has no solution.
Answer:
The value of \(\sqrt{x+1}\) must be positive, which is then added to 2. The sum of two positive numbers is positive; therefore, the sum cannot equal 0.
Eureka Math Algebra 2 Module 1 Lesson 28 Exit Ticket Answer Key
Consider the radical equation 3\(\sqrt{6-x}\) + 4 = – 8.
Question 1.
Solve the equation. Next to each step, write a description of what is being done.
Answer:
3\(\sqrt{6-x}\) = 1 12 Subtract 4 from both sides.
\(\sqrt{6-x}\) = – 4 Divide both sides by 3 in order to isolate the radical.
6 – x = 16 Square both sides to eliminate the radical.
x = – 10 Subtract 6 from both sides and divide by – 1.
Question 2.
Check the solution.
Answer:
3\(\sqrt{6-(-10)}\) + 4 = 3\(\sqrt{16}\) + 4 = 3(4) + 4 = 16, and B – 8, so -10 is not a valid solution.
Question 3.
Explain why the calculation in Problem 1 does not produce a solution to the equation.
Answer:
Because the square root of a positive number is positive, 3\(\sqrt{6-x}\) will be positive. A positive number added to 4 cannot be – 8.