Engage NY Eureka Math Algebra 2 Module 1 Lesson 20 Answer Key
Eureka Math Algebra 2 Module 1 Lesson 20 Example Answer Key
Example 1
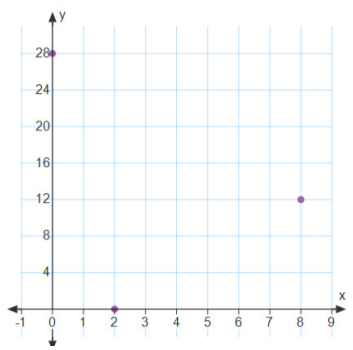
Find a polynomial P such that P(0) = 28, P(2) = 0, and P(8) = 12.
Answer:
Since P(0) = 28, c = 28 → P(x) = ax2 + bx+ 28
Since P(2) = 0 → 4a + 2b + 28 = 0, so 2a + b = – 14 (1)
Since P(8)= 12 → 64a + 8b + 28 = 12, so 8a + b = – 2 (2)
Subtract (1)from (2). → 6a = 12, so a = 2
Substitute to find b. → 2(2) + b = -14, so b = -18
P(x) = 2×22 – 18x + 28
Have students check their equation by finding P(0), P(2), and P(8) and showing that P(0) = 28, P(2) = 0, and P(8) = 12. Now work the problem again using the remainder theorem.
→ We can also use the remainder theorem to find the quadratic polynomial P that satisfies P(0) = 28, P(2) = 0, and P(8) = 12. We have already seen a technique that finds this quadratic polynomial, but the method using the remainder theorem generalizes to higher degree polynomials.
→ Use the first data point:
Since P(0) = 28, the remainder theorem tells us that for some polynomial a,
P(x) = (x – 0)a(x) + 28
= x a(x) + 28.
→ What do we know about the degree of the polynomial a? How do we know?
Since P will be a quadratic polynomial, a must be a linear polynomial.
→ Use the second data point:
Since P(2) = 0, we have
P(2) = 2a(2) + 28 = 0
2 a(2) = – 28
a(2) = – 14
Thus, the remainder theorem tells us that for some polynomial b,
a(x) = (x – 2) b(x) – 14.
→ What do we know about the degree of the polynomial b? How do we know?
Since a is a linear polynomial, b must be a constant polynomial.
→ Rewrite P in terms of b:
P(x) = x a(x) + 28
= x[(x – 2)b(x) – 14] + 28.
→ Use the third data point:
Since P(8) = 12, we have
P(8) = 8[(8 – 2) b(x) – 14] + 28 = 12
48b(x) – 104 + 28 = 12
48b(x) = 96
b(x) = 2.
→ Remember that we said the function b(x) would be constant, and we found that b(x) = 2 for all values of x.
→ Now we can rewrite the function P:
P(x) = x[(x – 2) b(x) – 14] + 28
= x[(x – 2)2 – 14] + 28.
→ Do the three points satisfy this equation?
P(0) = 0[(0 – 2) ∙ 2 – 14] + 28 = 28 ✓
P(2) = 2[(2 – 2) ∙ 2 – 14] + 28 = 0 ✓
P(8) = 8[(8 – 2) ∙ 2 – 141 + 28 = 12 ✓
→ For a final check, write the polynomial we just found in standard form.
P(x) = x[(x – 2)2 – 14] + 28
= 2x2 – 18x – 28.
Example 2.
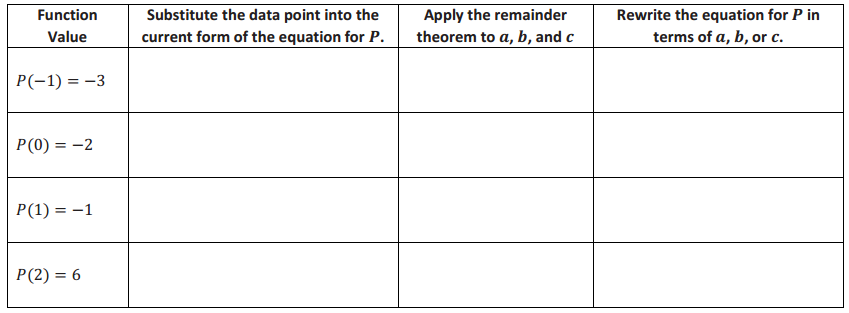
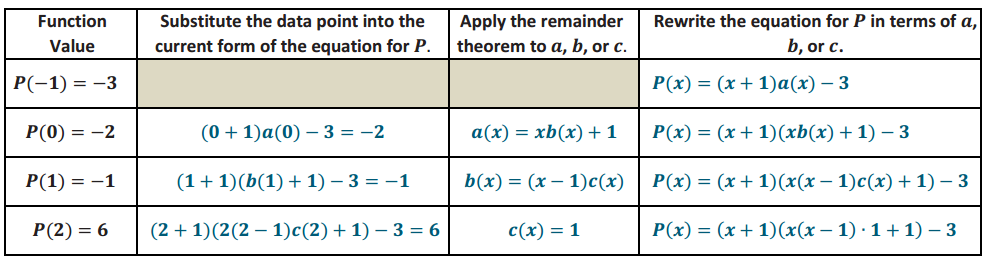
Find a degree 3 polynomial P such that P(- 1) = – 3, P(0) = – 2, P(1) = – 1, and P(2) = 6.
Answer:
→ Write the polynomial P in standard form.
P(x) = (x + 1) (x2 – x + 1) – 3
P(x) = x3 – x2 + x + x2 – x + 1 – 3
P(x) = x3 – 2
→ Verify that P satisfies the four given constraints.
P(-1) = (- 1)3 – 2 = – 3
P(0) = 03 – 2 = – 2
P(1) = 13 – 2 = – 1
P(2) = 23 – 2 = 6
Eureka Math Algebra 2 Module 1 Lesson 20 Mathematical Model Exercise Answer Key
The Environmental Protection Agency (EPA) is studying the flow of a river in order to establish flood zones. The EPA hired a surveying company to determine the flow rate of the river, measured as volume of water per minute. The firm set up a coordinate system and found the depths of the river at five locations as shown on the graph below. After studying the data, the firm decided to model the riverbed with a polynomial function and divide the cross-sectional area into six regions that are either trapezoidal or triangular so that the overall area can be easily estimated. The firm needs to approximate the depth of the river at two more data points in order to do this.
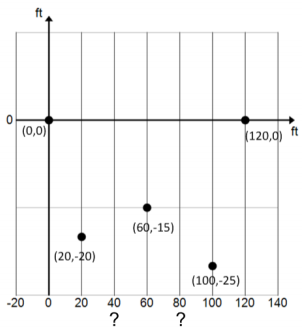
Answer:
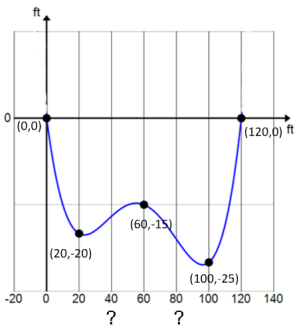
Draw the four trapezoids and two triangles that will be used to estimate the cross-sectional area of the riverbed.
Answer:
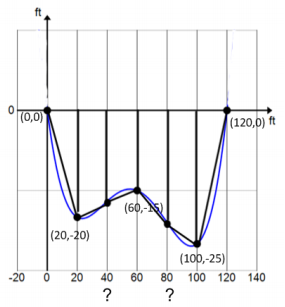
Eureka Math Algebra 2 Module 1 Lesson 20 Problem Set Answer Key
Question 1.
Suppose a polynomial function P is such that P(2) = 5 and P(3) = 12.
a. What is the largest-degree polynomial that can be uniquely determined given the information?
Answer:
Degree one
b. Is this the only polynomial that satisfies P(2) = 5 and P(3) = 12?
Answer:
No, there are an infinite number of polynomials that pass through those two points. However, two points will determine a unique equation for a linear function.
c. Use the remainder theorem to find the polynomial P of least degree that satisfies the two points given.
Answer:
P(x) = 7x – 9
d. Verify that your equation is correct by demonstrating that it satisfies the given points.
Answer:
P(2) = 7(2) – 9 = 5
P(3) = 7(3) – 9 = 12
Question 2.
Write a quadratic function P such that P(0) = – 10, P(5) = 0, and P(7) = 18 using the specified method.
a. Setting up a system of equations
Answer:
P(x) = x2 – 3x – 10
b. Using the remainder theorem
Answer:
P(x) = x2 – 3x – 10
Question 3.
Find a degree-three polynomial function P such that P(- 1) = 0, P(0) = 2, P(2) = 12, and P(3) = 32. Use the table below to organize your work. Write your answer in standard form, and verify by showing that each point satisfies the equation.
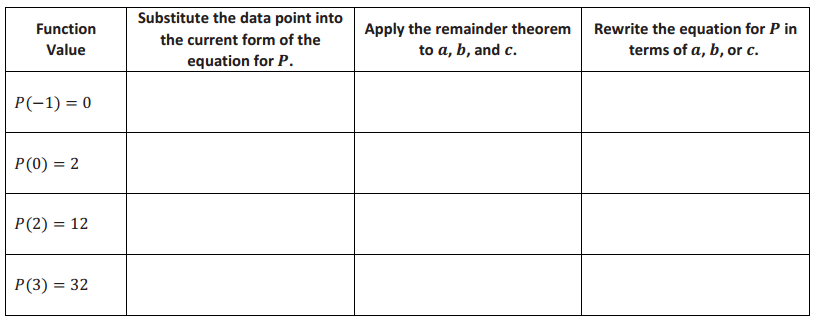
Answer:
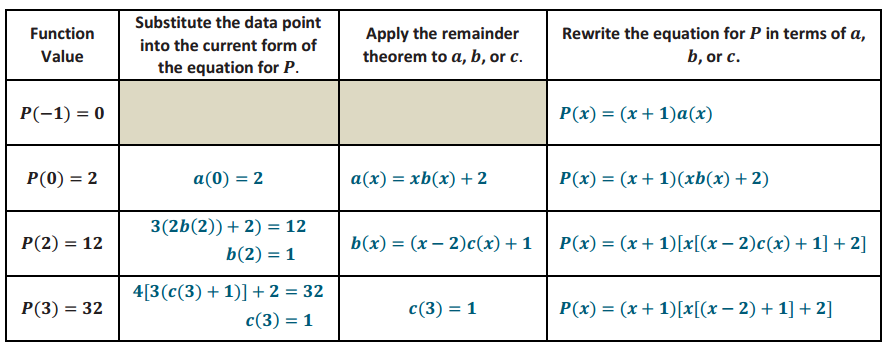
P(x) = x3 + x + 2 ✓
P(-1) = – 1 – 1 – 4 – 2 = 0 ✓
P(0) = 0 + 0 + 2 = 2 ✓
P(2) = 8 + 2 + 2 = 12 ✓
P(3) = 27 + 3 + 2 = 32 ✓
Question 4.
The method used in Problem 3 Is based on the Lagrange interpolation method. Research Joseph-Louis Lagrange, and write a paragraph about his mathematical work.
Answer:
Answers will vary.
Eureka Math Algebra 2 Module 1 Lesson 20 Exit Ticket Answer Key
Use the remainder theorem to find a quadratic polynomial P so that P(1) = 5, P(2) = 12, and P(3) = 25. Give your answer in standard form.
Answer:
Since P(1) = S, there is a linear polynomial a so that P(x) = (x – 1)a(x) + 5.
Since P(2) = 12, we have P(2) = (2 – 1)a(2) + 5 = 12, so a(2) = 7.
Because a(2) = 7, there exists a constant b so that a(x) = (x – 2)b + 7.
Substituting into P(x) gives P(x) = (x – 1)[(x – 2)b + 7].
Since P(3) = 25, we have P(3) = (3 – 1) [(3 – 2)b + 7] = 25. Solving for b gives b = 3.
It follows that P(x) = (x – 1)[(x – 2)3 + 7], and in standard form we have P(x) = 3x2 – 2x + 4.