Eureka Math Algebra 2 Module 1 Lesson 10 Answer Key

Engage NY Eureka Math Algebra 2 Module 1 Lesson 10 Answer Key

Eureka Math Algebra 2 Module 1 Lesson 10 Example Answer Key

Example 1
Prove that if x > 1, then a triangle with side lengths x² – 1, and x² + 1 is a right triangle.

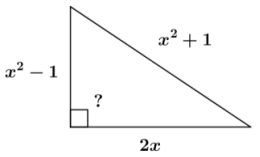
If x > 1, is this triangle right?
Answer:
Note: By the converse to the Pythagorean theorem, if a² + b² = c², then a triangle with side lengths a, b, c is a right triangle with a right angle opposite the side of length c. We are given that the triangle exists with these side lengths, so we do not need to explicitly verify that the lengths are positive. Therefore, we need only check that for any x > 1, we have (x² – 1)² + (2x)² = (x² + 1)².
PROOF: We are given a triangle with side lengths 2x, x² – 1 and x² + 1 for some real number x > 1. We need to show that the three lengths 2x, x² – 1, and x² + 1 form a Pythagorean triple. We will first show that (2x)² is equivalent to
(x² + 1)² – (x² – 1)².
(x² + 1)² – (x² – 1)² = ((x² + 1) + (x² – 1)) ((x² + 1) – (x² – 1)
= (2x²) (2)
= 4x²
= (2x)²
Since (2x)² = (x² + 1)² – (x² – 1)², we have shown that (x² – 1)² + (2x)² = (x² + 1)², and thus the numbers x² – 1, 2x, and x² + 1 form a Pythagorean triple. Then by the converse of the Pythagorean theorem, a triangle with sides of length 2x, x² – 1 and x² + 1 for some x > 1 is a right triangle.

Example 2.
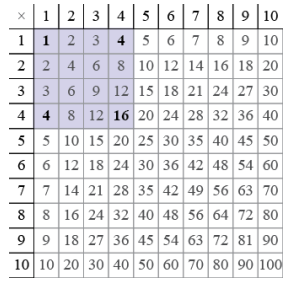
Next we describe an easy way to find Pythagorean triples using the expressions from Example 1. Look at the multiplication table below for {1, 2, ……,9}. Notice that the square numbers {1, 4, 9, ……, 81} lie on the diagonal of this table.
a. What value of x is used to generate the Pythagorean triple (15, 8, 17). by the formula (x² – 1, 2x, x² + 1)? How do the numbers (1, 4, 4, 16) at the corners of the shaded square in the table relate to the values 15, 8, and 17?

Answer:
Using the value 4 for x gives the triple (15, 8, 17) We see that 1 = 1² and 16 = 4², and then we can take 16 – 1 = 15, and 16 + 1 = 17. We also have 4 + 4 = 8.

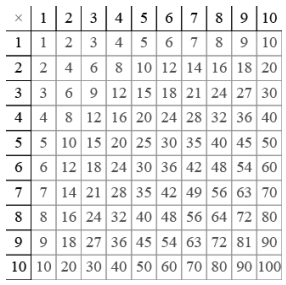
b. Now you try one. Form a square on the multiplication table below whose left-top corner is the 1 (as in the
example above) and whose bottom-right corner is a square number. Use the sums or differences of the numbers at the vertices of your square to form a Pythagorean triple. Check that the triple you generate is a Pythagorean triple.

Answer:
Answers will vary. Ask students to report their answers. For example, a student whose square has the bottom-right number 36 will generate 36 – 1 = 35, 6 + 6 = 12 and 36 + 1 = 37. Have students check that (12, 35, 37) is indeed a Pythagorean triple:
12² + 35² = 1369, and 36² = 1369

Let’s generalize this square to any square in the multiplication table where two opposite vertices of the square are square numbers.

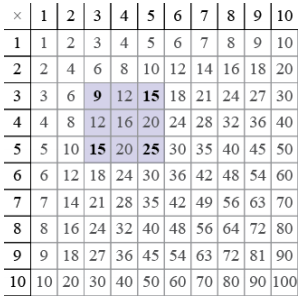
c. How can you use the sums or differences of the numbers at the vertices of the shaded square to get a triple (16, 30, 34)? Is it a Pythagorean triple?

Answer:
Following what we did above, take 25 – 9 = 16, 15 + 15 = 30, and 25 + 9 = 34, to get the triple (16, 30, 34). Yes, it is a Pythagorean triple: 16² + 30² = 900 + 256 = 1156 = 34²

d. Using x instead of 5 and y instead of 3 in your calculations in part (c), write down a formula for generating Pythagorean triples in terms of x and y.
Answer:
The calculation 25 – 9 generalizes to x² – y² as the length of one leg. The length of the other leg can be found by 15 + 15 = 2(3 ∙ 5), which generalizes to 2xy. The length of the hypotenuse, 25 + 9 generalizes to x² + y² It seems that Pythagorean triples can be generated by triples (x² – y², 2xy, x² + y²) where x > y > 0.

Eureka Math Algebra 2 Module 1 Lesson 10 Opening Exercise Answer Key

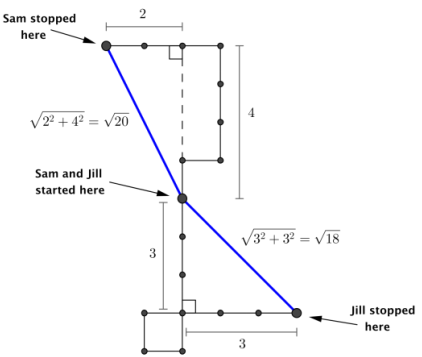
Sam and Jill decide to explore a city. Both begin their walk from the same starting point.
Sam walks 1 block north, 1 block east, 3 blocks north, and 3 blocks west.
Jill walks 4 blocks south, 1 block west, 1 block north, and 4 blocks east.
If all city blocks are the same length, who is the farthest distance from the starting point?
Answer:
Sam’s distance: ?20 city block lengths
Jill’s distance: ?18 city block lengths
Sam was farthest away from the starting point.

Eureka Math Algebra 2 Module 1 Lesson 10 Problem Set Answer Key

Question 1.
Rewrite each expression as a sum or difference of terms.
a. (x – 3) (x + 3)
Answer:
x² – 9

b. (x² – 3) (x² + 3)
Answer:
x⁴ – 9

c. (x¹⁵ + 3) (x¹⁵ – 3)
Answer:
x³⁰ – 9

d. (x – 3) (x² + 9) (x + 3)
Answer:
x⁴ – 81

e. (x² + y²) (x² – y²)
Answer:
x⁴ – y⁴

f. (x² + y²)²
Answer:
x⁴ + 2x²y² + y⁴

g. (x – y)² (x + y)²
Answer:
x⁴ – 2x²y² + y⁴

h. (x – y)² (x² + y²)² (x + y)²
Answer:
x⁸ – 2x⁴y⁴ + y⁸

Question 2.
Tasha used a clever method to expand (a + b + c) (a + b – c). She grouped the addends together like this [(a + b) + c] [(a + b) – c] and then expanded them to get the difference of two squares:
(a + b + c) (a + b – c) = [(a + b) + c] [(a + b) – c] = (a + b)² – c² = a² + 2ab + b² – c².
a. Is Tasha’s method correct? Explain why or why not.
Answer:
Yes, Tasha is correct. Expanding in the traditional way gives the same result.
(a + b + c) (a + b – c) = (a + b + c)a + (a + b + c)b + (a + b + c)c
= a² + ba + ca + ab + b² + cb – ac – bc – c²
= a² + 2ab + b² – c²

b. Use a version of her method to find (a + b + c) (a – b – c)
Answer:
(a + (b + c)) (a – (b + c)) = a² – (b + c)² = a² – b² – 2bc – c²

c. Use a version of her method to find (a + b – c) (a – b + c).
Answer:
(a + (b – c)) (a – (b – c)) = a² – (b – c)² = a² – b² – 2bc – c²

Question 3.
Use the difference of two squares identity to factor each of the following expressions.
a. x² – 81
Answer:
(x – 9) (x + 9)

b. (3x + y)² – (2y)²
Answer:
(3x – y)(3x + 3y) = 3(3x – y)(x + y)

c. 4 – (x – 1)²
Answer:
(3 – x) (1 + x)

d. (x + 2)² – (y + 2)²
Answer:
(x – y) (x + y + 4)

Question 4.
Show that the expression (x + y) (x – y) – 6x + 9 may be written as the difference of two squares, and then factor the expression.
Answer:
(x + y) (x – y) – 6x + 9 = x² – y² – 6x + 9 = (x² – 6x + 9) – y² = (x – 3)² – y² = (x – 3 – y) (x – 3 + y)

Question 5.
Show that (x + y)² – (x – y)² = 4xy for all real numbers x and y.
Answer:
(x + y)² – (x – y)² = [(x + y) – (x – y)] [(x + y) + (x – y)] = (2y) (2x) = 4x

Question 6.
Prove that a triangle with side lengths x² – y², 2xy, and x² + y² with x > y > 0 is a right triangle.
Answer:
The proof should look like the proof in Example 1 but with y instead of 1.

Question 7.
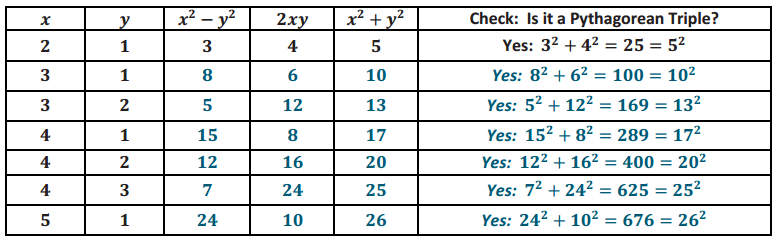
Complete the table below to find Pythagorean triples (the first row is done for you).

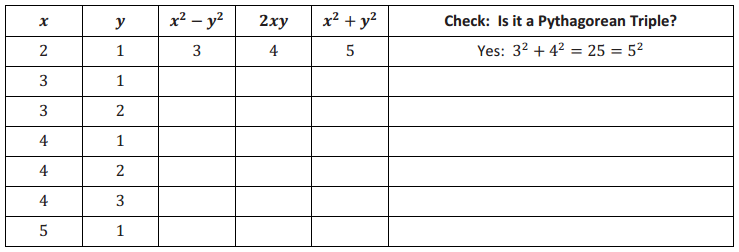
Answer:

Question 8.
Answer the following parts about the triple (9, 12, 15).
a. Show that (9, 12, 15) is a Pythagorean triple.
Answer:
We see that 9² + 12² = 81 + 144 = 225 and 15² = 225 so 9² + 12² = 15².

b. Prove that neither (9, 12, 15) nor (12, 9, 15) can be found by choosing a pair of integers x and y with x > y
and computing (x² – y², 2xy, x² + y²).
(Hint: What are the possible values of x and y if 2xy = 12? What about If 2xy = 9?)
Answer:
PROOF: Since 9 is odd and 2xy is even, there are no integer values of x and y that satisfy 2xy = 9. Thus, our
formula cannot generate the triple (12, 9, 15). Now suppose x andy are integers such that 2xy = 12. Thus
xy = 6 and x > y. There are only two possibilities: either x = 6 and y = 1, or x = 3 and y = 2. In the first
case, our formula generates the triple (6² – 1, 2 ∙ 6 ∙ 1, 6² + 1) = (35, 12, 37). In the second case, our formula generates the triple (3² – 2², 2 ∙ 3 ∙ 2, 3² + 2²) = (5, 12, 13). Thus, there is no way to generate the triple (9, 12, 15) using this method, even though it is a Pythagorean triple.

c. Wouldn’t it be nice if all Pythagorean triples were generated by (x² – y², 2xy, x² + y²)? Research Pythagorean triples on the Internet to discover what is known to be true about generating all Pythagorean triples using this formula.
Answer:
All Pythagorean triples are some multiple of a Pythagorean triple generated using this formula. For example, while (9, 12, 15) is not generated by the formula, it is a multiple of a Pythagorean triple (3, 4, 5) which is generated by the formula.

Question 9.
Follow the steps below to prove the identity (a² + b²) (x² + y²) = (ax – by)² + (bx + ay)².
a. Multiply (a² + b²) (x² + y²).
Answer:
(a² + b²) (x² + y²) = a²x² + a²y² + b²x² + b²y²

b. Square both binomials in (ax – by)² + (bx + ay)² and collect like terms.
Answer:
(ax – by)² + (bx + ay)² = a²x² – 2ax by + b²y² + b²x² + 2axby + a²y²
= a²x² + a²y² + b²x² + b²y²

c. Use your answers from part (a) and part (b) to prove the identity.
Answer:
(a² + b²)(x² + y²) = a²x² + a²y² + b²x² + b²y²
= (ax – by)² + (bx + ay)²

Question 10.
Many U.S. presidents took great delight in studying mathematics. For example, President James Garfield, while still a congressman, came up with a proof of the Pythagorean theorem based upon the ideas presented below.
In the diagram, two congruent right triangles with side lengths a, b and hypotenuse c, are used to form a trapezoid PQRS composed of three triangles.

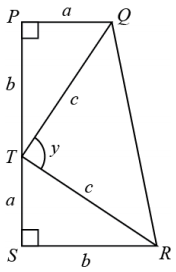
a. Explain why ∠QTR is a right angle.
Answer:
Since ∠TSR is a right angle, the measures of ∠STR and ∠SRT sum to 90°, so ∠STR and ∠SRT are complementary angles. Since ∆ TSR ≅ ∆ QPT by SSS triangle congruence, we have ∠STR ≅ ∆ PTQ. Thus, ∠PTQ and ∠STR must also be complementary. By the angle sum properties,

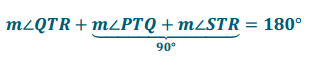
so that
m∠QTR + 90° = 180°
and we have shown that m∠QTR + 90° Thus, ∠QTR is a right angle.

b. What are the areas of ∆STR, ∆PTQ and ∆QTR in terms of a, b and c?
Answer:
We see that A(∆ STR) = \(\frac{1}{2}\)ab, A(∆ PTQ) = \(\frac{1}{2}\)ab, and because ∠QTR is a right angle, A(∆ QTR) = \(\frac{1}{2}\)c²

c. Using the formula for the area of a trapezoid, what is the total area of trapezoid PQRS in terms of a and b?
Answer:
A(PQRS) = \(\frac{1}{2}\) (a + b) (a + b)

d. Set the sum of the areas of the three triangles from part (b) equal to the area of the trapezoid you found in part (c), and simplify the equation to derive a relationship between a, b and c. Conclude that a right triangle with legs of length a and b and hypotenuse of length c must satisfy the relationship a² + b² = c².
Answer:
Equate areas:
\(\frac{1}{2}\)ab + \(\frac{1}{2}\)ab + \(\frac{1}{2}\)c² = \(\frac{1}{2}\)(a + b) (a + b),
ab + \(\frac{1}{2}\)c² = \(\frac{1}{2}\)(a² + 2ab + b²).
Multiply both sides by 2,
2ab + c² = a² + 2ab + b²,
and subtract 2ab from both sides,
c² = a² + b².

Eureka Math Algebra 2 Module 1 Lesson 10 Exit Ticket Answer Key

Question 1.
Generate six Pythagorean triples using any method discussed during class. Explain each method you use.
Answer:
Answers will vary. One example should use either (x² – 1, 2x, x² + 1) or (x² – y², 2xy, x² + y²) but after that students
can use the fact that a multiple of a Pythagorean triple is again a Pythagorean triple.