Eureka Math Algebra 1 Module 5 Lesson 5 Answer Key

Engage NY Eureka Math Algebra 1 Module 5 Lesson 5 Answer Key

Eureka Math Algebra 1 Module 5 Lesson 5 Example Answer Key

Example 1.
Determine whether the sequence below is arithmetic or geometric, and find the function that will produce any given term in the sequence:
16, 24, 36, 54, 81, …
Is this sequence arithmetic?
Answer:
The differences are 8, 12, 18, 27, … so right away we can tell this is not arithmetic; there is no common difference.

Is the sequence geometric?
Answer:
The ratios are all 1.5, so this is geometric.

What is the analytical representation of the sequence?
Answer:
Since the first term is 16 and the common ratio is 1.5, we have f(n) = 16(1.5)^{(n – 1)}.

Eureka Math Algebra 1 Module 5 Lesson 5 Exercise Answer Key

Exercises
Look at the sequence and determine the analytical representation of the sequence. Show your work and reasoning.
Exercise 1.
A decorating consultant charges $50 for the first hour and $2 for each additional whole hour. How much would 1, 000 hours of consultation cost?

Answer:
By subtracting, we see that this is an arithmetic sequence where we are adding 2 but starting at 50.
f(n) = 50 + 2(n – 1) = 48 + 2n
f(1000) = 48 + 2(1000) = 2048
1, 000 hours of consultation would cost $2, 048.

Exercise 2.
The sequence below represents the area of a square whose side length is the diagonal of a square with integer side length n. What would be the area for the 100th square? Hint: You can use the square below to find the function model, but you can also just use the terms of the sequence.

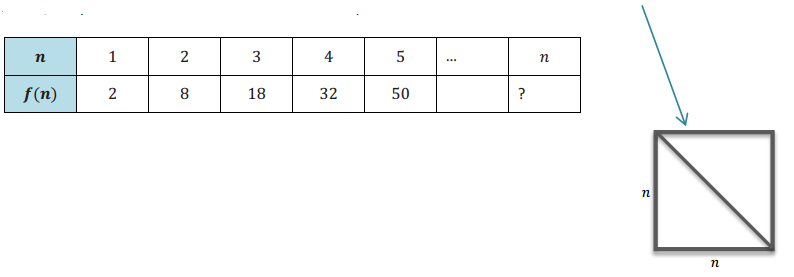
Answer:
Looking at first differences, we see that they are not the same (no common difference):
6, 10, 14, 18, ….
When we look for a common ratio, we find that the quotients of any two consecutive terms in the sequence are not the same: \(\frac{8}{2}\) ≠ \(\frac{18}{8}\) ≠ \(\frac{32}{18}\) ≠⋯
However, I noticed that the first difference increases by 4. This is an indication of a quadratic sequence, and the function equation must have a n². But since for n = 1 we would have n² = 1, we must need to multiply that by 2 to get the first term. Now, check to see if 2n² will work for the other terms.
f(n) = 2n²
Checking: (f(2) = 2(2² ) = 8
f(3) = 2(3² ) = 18
Yes! It works. So, f(100) = 2(100)² = 20 000.
Therefore, the area of the 100th square is 20, 000 square units.

Exercise 3.
What would be the tenth term in the sequence?

Answer:
There is no common difference. But the ratios are as follows: \(\frac{6}{3}\) = 2, \(\frac{12}{6}\) = 2, \(\frac{24}{12}\) = 2, …. This is a geometric sequence with a common ratio of 2. And the terms can be written as shown below.

The tenth term in the sequence is 3(512) or 1536.

Eureka Math Algebra 1 Module 5 Lesson 5 Problem Set Answer Key

Solve the following problems by finding the function/formula that represents the nth term of the sequence.
Question 1.
After a knee injury, a jogger is told he can jog 10 minutes every day and that he can increase his jogging time by
2 minutes every two weeks. How long will it take for him to be able to jog one hour a day?

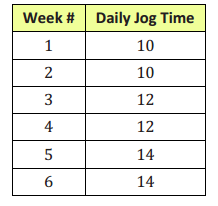
Answer:
This is an arithmetic sequence where the minutes increase by 2 every two weeks. (Note: We can either let 2n represent the number of weeks or let n represent a two – week period. Either way, we will end up having to compensate after we solve.) Let’s try it with n representing a two – week period:

f(n) = initial time + (n – 1)(common difference)
60 = 10 + (n – 1)(2) → 60 = 10 + 2n – 2 → 60 = 2n + 8
2n + 8 = 60 → 2n = 52 → n = 26
At the beginning of the 26^th 2 – week period, the jogger will be able to jog for 60 minutes. This will occur after 25 weeks ⋅2, or 50 weeks, or at the beginning of the 51st week.

Question 2.
A ball is dropped from a height of 10 feet. The ball then bounces to 80% of its previous height with each subsequent bounce.
a. Explain how this situation can be modeled with a sequence.
Answer:
According to the problem, to find the next height, multiply the current height by 0.8. This means the sequence is geometric.

b. How high (to the nearest tenth of a foot) does the ball bounce on the fifth bounce?
Answer:
f(n) = (initial height) (common ratio)^n for n bounces.
f(5) = 10(0.8)⁵ = 3.2768
The ball bounces approximately 3.3 feet on the fifth bounce.

Question 3.
Consider the following sequence:
8, 17, 32, 53, 80, 113, …

a. What pattern do you see, and what does that pattern mean for the analytical representation of the function?
Answer:
Difference of the differences is 6. Since the second difference is a nonzero constant, then the pattern must be quadratic.

b. What is the symbolic representation of the sequence?
Answer:
Sample response: 3n² does not work by itself. (If n = 1, then 3n² would be 3, but we have an 8 for the first term.) So, there must be a constant that is being added to it. Let’s test that theory:
(f(n) = 3n² + b
f(1) = 3(1)² + b = 8
3 + b = 8
+ b = 5
So, the terms of the sequence can be found using the number of the term, as follows:
f(n) = 3n² + 5
We can easily check to see if this function generates the sequence, and it does.

Question 4.
Arnold wants to be able to complete 100 military – style pull – ups. His trainer puts him on a workout regimen designed to improve his pull – up strength. The following chart shows how many pull – ups Arnold can complete after each month of training. How many months will it take Arnold to achieve his goal if this pattern continues?

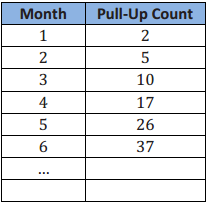
Answer:
This pattern does not have a common difference or a common ratio. When we look at the first differences (3, 5, 7, 9, 11, …), we see that the second differences would be constant (2, 2, 2, …). That means this is a quadratic sequence with n² in the nth term formula. For n = 1 we have 1² = 1, so we need to add 1 to get the first term to be 2. So, in general, we have the function f(n) = n² + 1. Let’s test that on the other terms:

2² + 1 = 5, 3² + 1 = 10, …. Yes, it works.
Now we need to find out which month (n) will produce 100 as the resulting number of pull – ups:
n² + 1 = 100 → n = \(\sqrt{99}\) ≈ 9.9
So, if this trend continues, at 10 months, Arnold will be able to complete 100 pull – ups.

Eureka Math Algebra 1 Module 5 Lesson 5 Exit Ticket Answer Key

Question 1.
A culture of bacteria doubles every 2 hours.
a. Explain how this situation can be modeled with a sequence.
Answer:
To find the next number of bacteria, multiply the previous number by 2. This situation can be represented by a geometric sequence. There will be a common ratio between each term of the sequence.

b. If there are 500 bacteria at the beginning, how many bacteria will there be after 24 hours?
Answer:
Using the exponential function f(n) = a ∙ bⁿ, where n represents the number of times the bacteria culture doubles, a represents the amount when n = 0, so a = 500. b is the growth rate, so b = 2.
f(n) = 500 ∙ 2ⁿ
f(n) = 500 ∙ 2¹² = 2 048 000
After 24 hours, there will be 2,048,000 bacteria.