Engage NY Eureka Math Algebra 1 Module 5 Lesson 3 Answer Key
Eureka Math Algebra 1 Module 5 Lesson 3 Example Answer Key
Example 1.
Gregory plans to purchase a video game player. He has $500 in his savings account and plans to save $20 per week from his allowance until he has enough money to buy the player. He needs to figure out how long it will take. What type of function should he use to model this problem? Justify your answer mathematically.
Answer:
→ Gregory decides that the exponential function can best represent the situation. Do you agree or disagree? Why? Support your answer mathematically.
I disagree because Gregory’s money increases at a constant rate of $20 a week with a starting balance of $500. The graph of the amount of money that Gregory saves over a period of time is a linear model.
→ What are the variables and quantities of this problem?
The rate is $20 per week, w is the number of weeks, and the initial value is $500.
→ What function represents the amount of Gregory’s money over a period of time (in weeks)?
The model is f(w) = 20w + 500. If the function is graphed, the slope of the line is 20 to reflect the constant rate of $20/week, and the y – intercept is $500, the initial amount.
Example 2.
One of the highlights in a car show event is a car driving up a ramp and flying over approximately five cars placed end – to – end. The ramp is 8 ft. at its highest point, and there is an upward speed of 88 ft/sec before it leaves the top of the ramp. What type of function can best model the height, h, in feet, of the car t seconds after leaving the end of the ramp? Justify your answer mathematically.
Answer:
→ What type of function can best model the height, h, in feet, of the car t seconds after leaving the end of the ramp? What were your clues? Justify your answer mathematically.
Quadratic function. This is an object in motion problem. The car would leave the ramp in an upward and forward motion and then, after travelling higher for a short time, would begin the fall due to the force of gravity.
→ What form would the equation take?
Since the distance is measured in feet and the time in seconds, we would use
h(t) = – 16t2 + v0 t + h0, and the equation would be h(t) = – 16t2 + 88t + 8.
Example 3.
Margie got $1,000 from her grandmother to start her college fund. She is opening a new savings account and finds out that her bank offers a 2% annual interest rate, compounded monthly. What type of function would best represent the amount of money in Margie’s account? Justify your answer mathematically.
Answer:
→ What type of function would best represent the amount of money in Margie’s account? Justify your answer mathematically.
Exponential Function. The amount of deposited money grows over time at a constant rate, and the pattern can be best described by an exponential function, f(x) = abx, where a represents the initial investment, and b is the expression (1 + \(\frac{r}{n}\)) as defined in the compounded interest formula:
P(t) = P0 (1 + \(\frac{r}{n}\))nt.
→ What function represents the amount of money deposited in the bank compounded monthly at the rate of 2%, if the initial amount of deposit was $1,000?
A(n) = 1000(1 + \(\frac{0.02}{12}\))12t
Note that we do not know how long Margie plans to leave the money in her account, so we do not know what the value of t is yet.
Remind students that percentages, in most cases, must be changed to decimals when used in exponential expressions.
Eureka Math Algebra 1 Module 5 Lesson 3 Exercise Answer Key
Exercises
Exercise 1.
City workers recorded the number of squirrels in a park over a period of time. At the first count, there were 15 pairs of male and female squirrels (30 squirrels total). After 6 months, the city workers recorded a total of 60 squirrels, and after a year, there were 120.
a. What type of function can best model the population of squirrels recorded over a period of time, assuming the same growth rate and that no squirrel dies?
Answer:
Exponential function
b. Write a function that represents the population of squirrels recorded over x number of years. Explain how you determined your function.
Answer:
Students may use the general exponential function f(x) = abx, by figuring out that this is a doubling exponential problem (in this case, the number of squirrels doubles every 6 months). So, the function would be f(x) = 30(2)2x because the squirrel population would double twice each year.
Exercise 2.
A rectangular photograph measuring 8 in by 10 in is surrounded by a frame with a uniform width, x.
a. What type of function can best represent the area of the picture and the frame in terms of x (the unknown frame’s width)? Explain mathematically how you know.
Answer:
This function can be best represented by a quadratic function because this is an area problem where the product of two linear measurements results in a quadratic.
b. Write an equation in standard form representing the area of the picture and the frame. Explain how you arrive at your equation.
Answer:
The dimensions of the picture are 8 in by 10 in. Taking into consideration the width of the frame, we have to add 2x to both the width and the length of the picture. Doing so results in (8 + 2x) and (10 + 2x). So, the area of the picture and the frame is A(x) = (8 + 2x)(10 + 2x) or A(x) = 4x2 + 36x + 80.
Exercise 3.
A ball is tossed up in the air at an initial rate of 50 ft/sec from 5 ft. off the ground.
a. What type of function models the height (h, in feet) of the ball after t seconds?
Answer:
Quadratic function
b. Explain what is happening to the height of the ball as it travels over a period of time (in t seconds).
Answer:
The initial height of the ball is 5 ft., and it travels upward with an initial velocity of 50 ft/sec. As time increases, the ball continues to travel upward, with the force of gravity slowing it down, until it reaches the maximum height and falls back to the ground.
c. What function models the height, h (in feet), of the ball over a period of time (in t seconds)?
Answer:
h(t) = – 16t2 + 50t + 5
Exercise 4.
A population of insects is known to triple in size every month. At the beginning of a scientific research project, there were 200 insects.
a. What type of function models the population of the insects after t years?
Answer:
Exponential function
b. Write a function that models the population growth of the insects after t years.
Answer:
Using the general form for exponential growth (b = 3), we have the initial population of 200 and 12t is the number of growth cycles over t years. The function would be f(t) = 200(3)12t.
P = P0 (1 + r)nt
P(t) = 200(1 + 2)12t, where r represents the growth rate at 200% and n = 12.
So, P(t) = 200(3)12t.
Eureka Math Algebra 1 Module 5 Lesson 3 Problem Set Answer Key
Question 1.
The costs to purchase school spirit posters are as follows: two posters for $5, four posters for $9, six posters for $13, eight posters for $17, and so on.
a. What type of function would best represent the cost of the total number of posters purchased?
Answer:
Linear function
b. What function represents the cost of the total number of posters purchased? How did you know? Justify your reasoning.
Answer:
Let x represent the number of school spirit posters. The four ordered pairs indicate a constant rate of change, (m = 2), so the equation is y = 2x + b. To find b, we need to substitute any ordered pair, say (2,5): 5 = 2(2) + b, so b = 1. The final equation for the function is f(x) = 2x + 1.
c. If you have $40 to spend, write an inequality to find the maximum number of posters you could buy.
Answer:
2x + 1 ≤ 40
Question 2.
NYC Sports Gym had 425 members in 2011. Based on statistics, the total number of memberships increases by 2% annually.
a. What type of function models the total number of memberships in this situation?
Answer:
Exponential function
b. If the trend continues, what function represents the total number of memberships in n years? How did you know? Justify your reasoning.
Answer:
f(n) = 425(1 + 0.02)n
The initial number of members is 425. The yearly growth rate of 2% means I have to multiply by 1.02 for each year. So, 1.02 will be the common ratio for this exponential function.
Question 3.
Derek throws a baseball upward from an initial height of 3 ft . The baseball hits the ground after 2 seconds.
a. What was the initial velocity of the baseball?
Answer:
h(t) = – 16t2 + v0t + 3
h(2) = – 16(2)2 + 2v0 + 3 = 0
v0 = 30.5
The initial velocity of the baseball was 0.5 ft/sec.
b. What is the function that models the height, h (in feet), of the baseball over a period of time t (in seconds)?
Answer:
h(t) = – 16t2 + 30.5t + 3
c. At what time did the baseball reach its maximum height? What was the maximum height of the baseball?
Answer:
The baseball reached its maximum height after 0.953125 seconds. The maximum height of the baseball was approximately 17.535 feet.
Eureka Math Algebra 1 Module 5 Lesson 3 Exit Ticket Answer Key
Question 1.
Create a model to compare these two texting plans :
a. Plan A costs $15 a month, including 200 free texts. After 200, they cost $0.15 each.
b. Plan B costs $20 a month, including 250 free texts. After 250, they cost $0.10 each.
Answer:
Monthly cost of Plan A: 
where t represents the number of texts per month
Monthly cost of Plan B: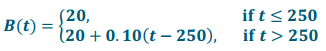 
where t represents the number of texts per month