Engage NY Eureka Math Algebra 1 Module 4 Lesson 7 Answer Key
Eureka Math Algebra 1 Module 4 Lesson 7 Example Answer Key
Example 1.
The length of a rectangle is 5 in. more than twice a number. The width is 4 in. less than the same number. If the area of the rectangle is 15 in2, find the unknown number.
Answer:
lw = A
(2n + 5)(n – 4) = 15
2n2 – 3n – 20 = 15
2n2 – 3n – 35 = 0
(2n + 7)(n – 5) = 0
n = 5 or – \(\frac{7}{2}\)
For this context (area), only positive values make sense. So, only n = 5 is possible.
Example 2.
A picture has a height that is \(\frac{4}{3}\) its width. It is to be enlarged so that the ratio of height to width remains the same, but the area is 192 in2. What are the dimensions of the enlargement?
Answer:
Let 4x to 3x represent the ratio of height to width. A = (h)(w), so we have
(4x)(3x) = 192
12x2 = 192
x = 4 or – 4,
which means that h = 16 and w = 12 because only positive values make sense in the context of area. Therefore, the dimensions of the enlargement are 16 inches and 12 inches.
Eureka Math Algebra 1 Module 4 Lesson 7 Exercise Answer Key
Opening Exercise
The length of a rectangle is 5 in. more than twice a number. The width is 4 in. less than the same number. The perimeter of the rectangle is 44 in. Sketch a diagram of this situation, and find the unknown number.
Answer:
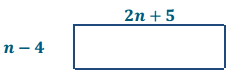
2l + 2w = P
2(2n + 5) + 2(n – 4) = 44
6n + 2 = 44
n = 7
Exercises
Solve the following problems. Be sure to indicate if a solution is to be rejected based on the contextual situation.
Exercise 1.
The length of a rectangle is 4 cm more than 3 times its width. If the area of the rectangle is 15 cm2, find the width.
Answer:
(4 + 3w)(w) = 15
3w2 + 4w – 15 = 0
(w + 3)(3w – 5) = 0
w = \(\frac{5}{3}\) or – 3
However, in this context only the positive value makes sense. Therefore, the width of the rectangle is \(\frac{5}{3}\) cm.
Exercise 2.
The ratio of length to width in a rectangle is 2:3. Find the length of the rectangle when the area is 150 in2.
Answer:
(2x)(3x) = 150
6x2 – 150 = 0
6(x2 – 25) = 0
6(x + 5)(x – 5) = 0
x = 5 or – 5
In this context, only positive values make sense, which means x = 5. Therefore, the length of the rectangle is 10 inches.
Exercise 3.
One base of a trapezoid is 4 in. more than twice the length of the second base. The height of the trapezoid is 2 in. less than the second base. If the area of the trapezoid is 4 in2, find the dimensions of the trapezoid.
(Note: The area of a trapezoid is A = \(\frac{1}{2}\)(b1 + b2)h.)
Answer:
A = \(\frac{1}{2}\) (b1 + b2 )h
4 = \(\frac{1}{2}\) (2b2 + 4 + b2)(b2 – 2)
4 = (\(\frac{3}{2}\) b2 + 2)(b2 – 2)
\(\frac{3}{2}\) b22 – b2 – 8 = 0
(\(\frac{3}{2}\) b2 – 4)(b2 + 2) = 0
b2 = \(\frac{8}{3}\) or – 2
However, only positive values make sense in this context. The first base is \(\frac{28}{3}\) in.; the second base is \(\frac{8}{3}\) in.; and the height is \(\frac{2}{3}\) in.
Exercise 4.
A garden measuring 12 m by 16 m is to have a pedestrian pathway that is w meters wide installed all the way around it, increasing the total area to 285 m2. What is the width, w, of the pathway?
Answer:
(12 + 2w)(16 + 2w) = 285
4w2 + 56w – 93 = 0
(2w + 31)(2w – 3) = 0
w = \(\frac{3}{2}\) or – \(\frac{31}{2}\)
However, only the positive value makes sense in this context, so the width of the pathway is \(\frac{3}{2}\) m.
Exercise 5.
Karen wants to plant a garden and surround it with decorative stones. She has enough stones to enclose a rectangular garden with a perimeter of 68 ft., and she wants the garden to cover 240 ft2. What is the length and width of her garden?
Answer:
68 = 2l + 2w
w = 34 – l
240 = (l)(34 – l)
l2 – 34l + 240 = 0
(l – 10)(l – 24) = 0
l = 10 or 24
Important to notice here is that both solutions are positive and could represent the length. Because length and width are arbitrary distinctions here, the garden measures 24 ft. × 10 ft., with either quantity representing the width and the other representing the length.
Exercise 6.
Find two consecutive odd integers whose product is 99. (Note: There are two different pairs of consecutive odd integers and only an algebraic solution will be accepted.)
Answer:
Let n represent the first odd integer and n + 2 represent the subsequent odd integer. The product is n(n + 2), which must equal 99.
n(n + 2) = 99
n2 + 2n – 99 = 0
(n – 9)(n + 11) = 0
n = 9 or n = – 11
If n = 9, then n + 2 = 11, so the numbers could be 9 and 11. Or if n = – 11, then n + 2 = – 9, so the numbers could be – 11 and – 9.
OR
Let 2n – 1 represent the first odd integer and 2n + 1 represent the subsequent odd integer. The product is
4n2 – 1, which must equal 99.
4n2 – 1 = 99
4n2 = 100
n2 = 25
n = ±5
The two consecutive pairs of integers would be
2(5) – 1 = 9; 2(5) + 1 = 11
AND
2( – 5) – 1 = – 11; 2(5) + 1 = – 9
Exercise 7.
Challenge: You have a 500 – foot roll of chain link fencing and a large field. You want to fence in a rectangular playground area. What are the dimensions of the largest such playground area you can enclose? What is the area of the playground?
Answer:
2w + 2l = 500, so w + l = 250, and l = 250 – w. A = (l)(w), so (250 – w)(w) = 0 gives us roots at w = 0 and w = 250. This means the vertex of the equation is
w = 125 → l = 250 – 125 = 125. The area of the playground will be 125 ft. × 125 ft., or 15,625 ft2.
Eureka Math Algebra 1 Module 4 Lesson 7 Problem Set Answer Key
Solve the following problems.
Question 1.
The length of a rectangle is 2 cm less than its width. If the area of the rectangle is 35 cm2, find the width.
Answer:
(w – 2)(w) = 35
w2 – 2w – 35 = 0
(w + 5)(w – 7) = 0
w = 7 or – 5
However, since the measurement can only be positive, the width is 7 cm.
Question 2.
The ratio of length to width (measured in inches) in a rectangle is 4:7. Find the length of the rectangle if the area is known to be 700 in2.
Answer:
(4x)(7x) = 700
28x2 – 700 = 0
28(x2 – 25) = 0
28(x + 5)(x – 5) = 0
x = 5 or – 5
However, the measure can only be positive, which means x = 5, and the length is 20 inches
Question 3.
One base of a trapezoid is three times the length of the second base. The height of the trapezoid is 2 in. smaller than the second base. If the area of the trapezoid is 30 in2, find the lengths of the bases and the height of the trapezoid.
Answer:
A = \(\frac{1}{2}\) (b1 + b2)h
30 = \(\frac{1}{2}\) (3b2 + b2 )(b2 – 2)
30 = (2b2 )(b2 – 2)
2b22 – 4b2 – 30 = 0
2(b2 – 5)(b2 + 3) = 0
b2 = 5 or – 3
However, only the positive value makes sense. The first base is 15 in.; the second base is 5 in.; and the height is 3 in.
Question 4.
A student is painting an accent wall in his room where the length of the wall is 3 ft. more than its width. The wall has an area of 130 ft2. What are the length and the width, in feet?
Answer:
(w + 3)(w) = 130
w2 + 3w – 130 = 0
(w + 13)(w – 10) = 0
w = 10 or – 13
However, since the measure must be positive, the width is 10 ft., and the length is 13 ft.
Question 5.
Find two consecutive even integers whose product is 80. (There are two pairs, and only an algebraic solution will be accepted.)
Answer:
(w)(w + 2) = 80
w2 + 2w – 80 = 0
(w + 10)(w – 8) = 0
w = 8 or – 10
So, the consecutive even integers are 8 and 10 or – 10 and – 8.
Eureka Math Algebra 1 Module 4 Lesson 7 Exit Ticket Answer Key
Question 1.
The perimeter of a rectangle is 54 cm. If the length is 2 cm more than a number, and the width is 5 cm less than twice the same number, what is the number?
Answer:
2l + 2w = P
2(n + 2) + 2(2n – 5) = 54
6n – 6 = 54
n = 10
Question 2.
A plot of land for sale has a width of x ft. and a length that is 8 ft. less than its width. A farmer will only purchase the land if it measures 240 ft2. What value for x causes the farmer to purchase the land?
Answer:
(x)(x – 8) = 240
x2. – 8x – 240 = 0
(x – 20)(x + 12) = 0
x = 20 or x = – 12
Since the answer cannot be negative, the answer is x = 20. The farmer will purchase the land if the width is 20 ft.