Eureka Math Algebra 1 Module 4 Lesson 3 Answer Key

Engage NY Eureka Math Algebra 1 Module 4 Lesson 3 Answer Key

Eureka Math Algebra 1 Module 4 Lesson 3 Example Answer Key

Example 1
In Lesson 2, we saw that factoring is the reverse process of multiplication. We factor a polynomial by reversing the distribution process.
Consider the following example of multiplication:
(x + 3)(x + 5) → x² + 5x + 3x + 15 → x² + 8x + 15.
When we compare the numbers in the factored form with the numbers in the expanded form, we see that 15 is the product of the two numbers (3⋅5), and 8 is their sum (3 + 5). The latter is even more obvious when we look at the expanded form before the like terms are combined.

Can you explain why that relationship exists between the numbers in the factors and the numbers in the final expanded form?
Answer:
The coefficient of the term with a variable to the first degree (the linear term), in this case 8, is the sum of the two constant terms of the binomials. The constant term of the quadratic expression is the product of the two constant terms of the binomials. (Make sure students observe a connection rather than merely memorizing a procedure.)

Example 2.
Now compare the expansion of this binomial product to the one above:
(2x + 3)(1x + 5) → 2x² + 10x + 3x + 15 → 2x² + 13x + 15.
In the expression lying between the two arrows (before the like terms are combined), we can see the coefficients of the “split” linear terms ( + 10x + 3x). Also notice that for this example, we have coefficients on both x – terms in the factors and that one of the coefficients is not 1. We have 2 and 1 as the factors of the leading coefficient in the expanded form and 3 and 5 as the factors of the constant term. Get ready for quadratic expressions in factored form where neither of the x – term coefficients are 1.

a. How is this product different from the first example? How is it similar?
Answer:
When comparing the factored forms, we see that they are the same except for the coefficient of the first factor in Example 2 (i.e., 2). (It is important to point out that the other factor has an x term with a coefficient of 1. There will be examples in the future where both x terms have coefficients other than 1.) When comparing the expanded forms of both examples (the green numbers), the quadratic term (i.e., 2x²) and one of the linear terms (i.e., 10x) are different in this example because of the new leading coefficient of 2. The other two terms in the expanded form (i.e., 3x and 15) were not affected by the leading coefficient. Point out that the differences are by a factor of 2.

b. Why are the “split” linear terms different in the two examples?
Answer:
In the first example, the linear coefficients are 5 and 3. For the second example, they are 10 and 3. (Most students will notice that both products have a 3x, but one has a 5x and the other a 10x, or 2(5x), for the other linear term. The difference is because of the leading coefficient, which doubled two of the four terms of the expanded expression between the two arrows.)

c. Now that we have four different numbers (coefficients) in each form of the expression, how can we use the numbers in the expanded form of the quadratic expression on the right to find the numbers in the factors on the left?
Answer:
We still know that the factor pairs of 15 are the only possibilities for two of the constant terms (1 and 15 or 3 and 5). However, we now have to use the 2 as a factor with one of them to find the sum. Here are all the possibilities:
( + 2)( + 1) + ( + 1)( + 15);
( + 2)( + 15) + ( + 1)( + 1);
( + 2)( + 5) + ( + 1)( + 3);
( + 2)( + 3) + ( + 1)( + 5).
Only one of these gives 13 for the middle – term coefficient: 2(5) + (1)(3) = 13.

d. Now we need to place those numbers into the parentheses for the factors so that the product matches the expanded form of the quadratic expression. Here is a template for finding the factors using what we call the product – sum method:
(__x ± __)(__x ± __) [We have four number places to fill in this factor template.]

(__x ± 3 )(__x ± 5 ) [We know that the 3 and 5 are the correct factors for 15, so we start there.]

( 2x ± 3 )( 1x ± 5 ) [We know that 2 and 1 are the only factors of 2, with the 2 opposite the 5 so that the distribution process gives us 10x for one product.]

( 2x + 3 )( x + 5 ) [Finally, we know, at least for this example, that all the numbers are positive.]

Example 3.
Now try factoring a quadratic expression with some negative coefficients: 3x² – x – 4.
(___x ± ___)(___x ± ___) [We have four number places to fill in this factor template.]

(___x ± 1 )(___x ± 4 ) [We know that ±1 and ±4 or ±2 and ±2 are the only possible factors for the constant term, – 4, so we start there. Try 1 and 4 to start, and if that does not work, go back and try ±2 and ±2. We know that only one of the numbers can be negative to make the product negative.]

( 1 x ± 1 )( 3 x ± 4 ) [We know that 3 and 1 are the only factors of 3. We also know that both of these are positive (or both negative). But we do not know which positions they should take, so we will try both ways to see which will give a sum of – 1.]

( x + 1 )( 3x – 4) [Finally, we determine the two signs needed to make the final product 3x² – x – 4.]

Eureka Math Algebra 1 Module 4 Lesson 3 Exercise Answer Key

Opening Exercise
Carlos wants to build a sandbox for his little brother. He is deciding between a square sandbox with side lengths that can be represented by x + 3 units and a rectangular sandbox with a length 1 unit more than the side of the square and width 1 unit less than the side of the square.

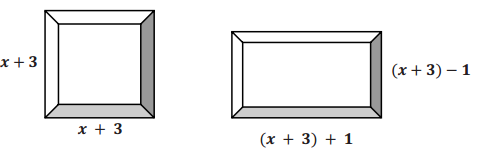
Carlos thinks the areas should be the same because one unit is just moved from one side to the other.
a. Do you agree that the two areas should be the same? Why or why not?
Answer:
Allow some class discussion of this question. Some students may agree, but it is unlikely that any students will have evidence to support their claim. Others may disagree but will also be unsure why they instinctively feel there will be a difference.

b. How would you write the expressions that represent the length and width of the rectangular sandbox in terms of the side length of the square?
Answer:
Students are likely to perform the calculation and give x + 4 and x + 2 as the length and width. Lead them to using (x + 3) as a separate entity with the length of the rectangle as (x + 3) + 1 and the width as (x + 3) – 1.

c. If you use the expressions for length and width represented in terms of the side length of the square, can you then write the area of the rectangle in the same terms?
Answer:
Area of the rectangle: [(x + 3) + 1][(x + 3) – 1]

d. How can this expression be seen as the product of a sum and difference: (a + b)(a – b)?
Answer:
This is (a + b)(a – b), where a = (x + 3) and b = 1.

e. Can you now rewrite the area expression for the rectangle as the difference of squares:
Answer:
(a + b)(a – b) = a² – b²?
(a + b)(a – b) = a² – b², so [(x + 3) + 1][(x + 3) – 1] = (x + 3)² – 1.

f. Look carefully at your answer to the last question. What does it tell you about the areas of the two shapes?
Answer:
Since the area of the square is (x + 3)² and the area of the rectangle is (x + 3)² – 1, this shows the area of the square (x + 3)² is one more square unit than the area of the rectangle.

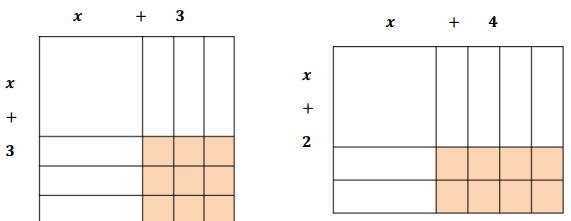
g. Can you verify that our algebra is correct using a diagram or visual display?
Answer:
Use the visual diagram below in the same configuration to demonstrate the difference visually. Notice that there is the same number of smaller shapes for x² and for x square units: 1 square each with x² square units and 6 small rectangles each with dimensions 1 by x, or x square units. However, if you count the smaller 1 by 1 square unit, the square has 9 and the rectangle has 8, making it 1 square unit less in area.

Exercises
For Exercises 1–6, factor the expanded form of these quadratic expressions. Pay particular attention to the negative and positive signs.
Exercise 1.
3x² – 2x – 8
Answer:
(3x + 4)(x – 2)

Exercise 2.
3x² + 10x – 8
Answer:
(x + 4)(3x – 2)

Exercise 3.
3x² + x – 14 [Notice that there is a 1 as a coefficient in this one.]
Answer:
(3x + 7)(x – 2)

Exercise 4.
2x² – 21x – 36 [This might be a challenge. If it takes too long, try the next one.]
Answer:
(2x + 3)(x – 12)

Exercise 5.
– 2x² + 3x + 9 [This one has a negative on the leading coefficient.]
Answer:
(2x + 3)( – x + 3)

Exercise 6.
r² + \(\frac{6}{4}\) r + \(\frac{9}{16}\) [We need to try one with fractions, too.]
Answer:
(r + \(\frac{3}{4}\))(r + \(\frac{3}{4}\))

For Exercises 7–10, use the structure of these expressions to factor completely.
Exercise 7.
100x² – 20x – 63
Answer:
(10x)² – 2(10x) – 63
Factored form: (10x + 7)(10x – 9)

Exercise 8.
y⁴ + 2y² – 3
Answer:
(y²)² + 2(y² ) – 3
(y² – 1)(y² + 3)
Factored form: (y – 1)(y + 1)(y² + 3)

Exercise 9.
9x² – 3x – 12
Answer:
(3x)² – (3x) – 12
(3x + 3)(3x – 4)
Factored form: 3(x + 1)(3x – 4)

Exercise 10.
16a² b⁴ + 20ab² – 6
Answer:
(4ab²)² + 5(4ab² ) – 6
(4ab² + 6)(4ab² – 1)
Factored form: 2(2ab² + 3)(4ab² – 1)

Eureka Math Algebra 1 Module 4 Lesson 3 Problem Set Answer Key

Factor the following quadratic expressions.
Question 1.
x² + 9x + 20
Answer:
(x + 4)(x + 5)

Question 2.
3x² + 27x + 60
Answer:
3(x + 4)(x + 5)

Question 3.
4x² + 9x + 5
Answer:
(4x + 5)(x + 1)

Question 4.
3x² – 2x – 5
Answer:
(3x – 5)(x + 1)

Question 5.
– 2x² + 5x
Answer:
x( – 2x + 5) or – x(2x – 5)

Question 6.
– 2x² + 5x – 2
Answer:
(x – 2)( – 2x + 1) or – (2x – 1)(x – 2)

Question 7.
5x² + 19x – 4
Answer:
(5x – 1)(x + 4)

Question 8.
4x² – 9
Answer:
(2x + 3)(2x – 3)

Question 9.
4x² – 12x + 9 [This one is tricky, but look for a special pattern.]
Answer:
(2x – 3)(2x – 3) or (2x – 3)²

Question 10.
3x² – 13x + 12
Answer:
(x – 3)(3x – 4)

Factor each expression completely.
Question 11.
a⁴ – b⁴
Answer:
a⁴ – b⁴ = (a² )² – (b² )² = (a² + b² )(a² – b² ) = (a² + b²)(a + b)(a – b)

Question 12.
16a⁴ – b⁴
Answer:
16a⁴ – b⁴ = (4a² )² – (b² )² = (4a² + b² )(4a² – b² ) = (4a² + b²)(2a + b)(2a – b)

Question 13.
a² – 5a + 4
Answer:
a² – 5a + 4 = (a – 4)(a – 1)

Question 14.
a⁴ – 5a² + 4
Answer:
a⁴ – 5a² + 4 = (a² )² – 5(a²) + 4 = (a² – 4)(a² – 1) = (a + 2)(a – 2)(a + 1)(a – 1)

Question 15.
9a² – 15a + 4
Answer:
9a² – 15a + 4 = (3a)² – 5(3a) + 4 = (3a – 4)(3a – 1)

Eureka Math Algebra 1 Module 4 Lesson 3 Exit Ticket Answer Key

Question 1.
Use algebra to explain how you know that a rectangle with side lengths one less and one more than a square will always be 1 square unit smaller than the square.
Answer:
If a is the length of the side of the square, then a² is the area of the square. The rectangle’s side lengths will be (a – 1) and (a + 1). That product, which represents the area of the rectangle, is a² – 1, or 1 square unit less than the area of the square.

Question 2.
What is the difference in the areas of a square and rectangle if the rectangle has side lengths 2 less and 2 more than a square? Use algebra or a geometric model to compare the areas and justify your answer.
Answer:
Using the same logic as for Problem 1, the rectangle dimensions will be (a + 2) and (a – 2) with an area of a² – 4. Therefore, the area of the rectangle is 4 square units less than the area of the original square.

Question 3.
Explain why the method for factoring shown in this lesson is called the product – sum method.
Answer:
It is called the product – sum method because you look for the two numbers with a product equal to the constant term of the quadratic expression and a sum equal to the coefficient of the linear term.