Engage NY Eureka Math Algebra 1 Module 4 Lesson 23 Answer Key
Eureka Math Algebra 1 Module 4 Lesson 23 Exercise Answer Key
Mathematical Modeling Exercise 1
Use the information in the Opening to answer the following questions.
Chris stands on the edge of a building at a height of 60 ft. and throws a ball upward with an initial velocity of 68 ft/s. The ball eventually falls all the way to the ground. What is the maximum height reached by the ball? After how many seconds will the ball reach its maximum height? How long will it take the ball to reach the ground?
a. What units will we be using to solve this problem?
Answer:
Feet for height, seconds for time, and feet per second for velocity
b. What information from the contextual description do we need to use in the function equation?
Answer:
Gravity = – 32 ft/s2
Initial Velocity (v0) = 68 ft/s
Initial Height (h0) = 60 ft.
So, the function is h(t) = – 16t2 + 68t + 60.
c. What is the maximum point reached by the ball? After how many seconds will it reach that height? Show your reasoning.
Answer:
The maximum function value is at the vertex. To find this value, we first notice that this function is factorable and is not particularly friendly for completing the square. So, we will rewrite the function in factored form, f(t) = – 4(4t2 – 17t – 15) f(t) = – 4(4t + 3)(t – 5).
Second, we find the zeros, or the t – intercepts, of the function by equating the function to zero (zero height).
So, – 4(4t + 3)(t – 5) = 0.
Then, (4t + 3) = 0 or (t – 5) = 0.
t – intercepts are t = – \(\frac{3}{4}\) or t = 5.
Then, using the concept of symmetry, we find the midpoint of the segment connecting the two t – intercepts (find the average of the t – coordinates): t = \(\frac{ – \frac{3}{4} + 5}{2}\) = 2 \(\frac{1}{8}\), or 2.125.
Now, we find h(2.125) in the original function, h(t) = – 16t2 + 68t + 60, h(2.125) = 132.25.
Therefore, the ball reached its maximum height of 132.25 ft. after 2.125 sec.
(Note that students may try to complete the square for this function. The calculations are very messy, but the results will be the same:
h(t) = – 16(t – \(\frac{17}{8}\))2 + \(\frac{529}{4}\) = – 16(t – 2.125)2 + 132.25. Students may also opt to use the vertex formula.)
d. How long will it take the ball to land on the ground after being thrown? Show your work.
Answer:
We factored in the previous question and found the zeros of this function to be t = – \(\frac{3}{4}\) and t = 5. The ball begins its flight at 0 sec. and ends at 5 sec. Therefore, it will be in flight for 5 sec.
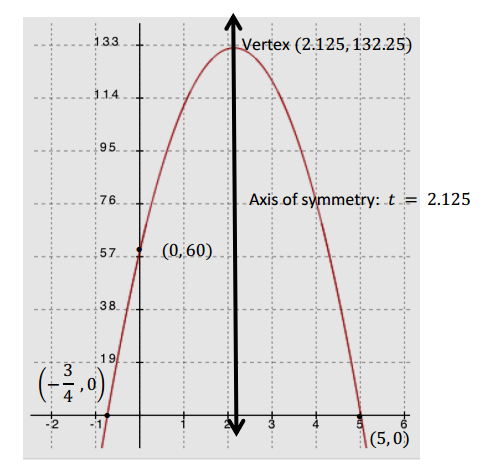
e. Graph the function of the height, h, of the ball in feet to the time, t, in seconds. Include and label key features of the graph such as the vertex, axis of symmetry, and t – and y – intercepts.
Answer:
The graph should include identification of the intercepts, vertex, and axis of symmetry.
Vertex: (2.125,132.25)
t – intercepts: ( – 0.75,0) and (5,0)
y – intercept: (0,60) (See the graph of y = h(t).)
Mathematical Modeling Exercise 2
Read the following information about Business Applications:
Many business contexts can be modeled with quadratic functions. This is because the expressions representing price (price per item), the cost (cost per item), and the quantity (number of items sold) are typically linear. The product of any two of those linear expressions will produce a quadratic expression that can be used as a model for the business context. The variables used in business applications are not as traditionally accepted as variables that are used in physics applications, but there are some obvious reasons to use c for cost, p for price, and q for quantity (all lowercase letters). For total production cost we often use C for the variable, R for total revenue, and P for total profit (all uppercase letters). You have seen these formulas in previous lessons, but we will review them here since we use them in the next two lessons.
Business Application Vocabulary
UNIT PRICE (PRICE PER UNIT): The price per item a business sets to sell its product, sometimes represented as a linear expression.
QUANTITY: The number of items sold, sometimes represented as a linear expression.
REVENUE: The total income based on sales (but without considering the cost of doing business).
UNIT COST (COST PER UNIT) OR PRODUCTION COST: The cost of producing one item, sometimes represented as a linear expression.
PROFIT: The amount of money a business makes on the sale of its product. Profit is determined by taking the total revenue (the quantity sold multiplied by the price per unit) and subtracting the total cost to produce the items (the quantity sold multiplied by the production cost per unit): Profit = Total Revenue – Total Production Cost.
The following business formulas will be used in this lesson:
Total Production Costs = (cost per unit)(quantity of items sold)
Total Revenue = (price per unit)(quantity of items sold)
Profit = Total Revenue – Total Production Costs
Now answer the questions related to the following business problem:
A theater decided to sell special event tickets at $10 per ticket to benefit a local charity. The theater can seat up to 1,000 people, and the manager of the theater expects to be able to sell all 1,000 seats for the event. To maximize the revenue for this event, a research company volunteered to do a survey to find out whether the price of the ticket could be increased without losing revenue. The results showed that for each $1 increase in ticket price, 20 fewer tickets will be sold.
a. Let x represent the number of $1.00 price – per – ticket increases. Write an expression to represent the expected price for each ticket.
Answer:
Let x represent the number of $1 increases. If each ticket is $10, plus a possible price increase in $1 increments, the price per ticket will be 10 + 1x.
b. Use the survey results to write an expression representing the possible number of tickets sold.
Answer:
Since 20 fewer seats will be sold for each $1 increase in the ticket price, 20x represents the number of seats fewer than 1,000 that will be sold.
1000 – 20x represents the expected number of tickets sold at this higher price.
c. Using x as the number of $1 – ticket price increases and the expression representing price per ticket, write the function, R, to represent the total revenue in terms of the number of $1 – ticket price increases.
Answer:
Total Revenue = (price per ticket)(number of tickets)
R(x) = (10 + x)(1000 – 20x) = 10 000 + 1000x – 200x – 20x2 = – 20x2 + 800x + 10 000
d. How many $1 – ticket price increases will produce the maximum revenue? (In other words, what value for x produces the maximum R value?)
Answer:
We need to find the vertex of the revenue equation. The equation is originally in factored form, so we can just go back to that form, or we can complete the square (which seems to be pretty efficient).
1. By completing the square: R(x) = – 20(x2 – 40x + ) + 10 000
– 20(x2 – 40x + 400) + 10 000 + 8000
– 20(x – 20)2 + 18 000, so the vertex is (20,18 000).
2. Using the factors, set the equation equal to zero to find the zeros of the function:
R(x) = (1000 – 20x)(10 + x) = 0
x = – 10 and 50 are the zeros, and the vertex will be on the axis of symmetry (at the midpoint between – 10 and 50), which is x = 20.
Finally, we reach the conclusion that after 20 price increases, the theater will maximize its revenue.
e. What is the price of the ticket that will provide the maximum revenue?
Answer:
Price per ticket expression is 10 + x. For x = 20, we have 10 + 20 = 30. The price per ticket that will provide the maximum revenue is $30.
f. What is the maximum revenue?
Answer:
According to the R – value at the vertex, the maximum revenue will be $18,000.
g. How many tickets will the theater sell to reach the maximum revenue?
Answer:
With the maximum revenue of $18,000 at $30/ticket, the theater is selling 600 tickets.
h. How much more will the theater make for the charity by using the results of the survey to price the tickets than they would had they sold the tickets for their original $10 price?
Answer:
At $10 per ticket, the theater would have brought in $10,000 after selling all 1,000 seats. The theater will make an additional $8,000 by using the survey results to price their tickets.
Exercise 1.
Two rock climbers try an experiment while scaling a steep rock face. They each carry rocks of similar size and shape up a rock face. One climbs to a point 400 ft. above the ground, and the other climbs to a place below her at 300 ft. above the ground. The higher climber drops her rock, and 1 second later the lower climber drops his. Note that the climbers are not vertically positioned. No climber is injured in this experiment.
a. Define the variables in this situation, and write the two functions that can be used to model the relationship between the heights, h1 and h2, of the rocks, in feet, after t seconds.
Answer:
h1 represents the height of the rock dropped by the higher climber,
h2 represents the height of the rock dropped by the lower climber,
t represents the number of seconds passed since the higher climber dropped her rock,
t – 1 represents the number of seconds since the lower climber dropped his rock.
h1 (t) = – 16t2 + 400 and h2 (t) = – 16(t – 1)2 + 300
b. Assuming the rocks fall to the ground without hitting anything on the way, which of the two rocks will reach the ground last? Show your work, and explain how you know your answer is correct.
Answer:
We are looking for the zeros in this case. Setting each function equal to zero we get:
h1 (t) = – 16t2 + 400 = 0
– 16(t2 – 25) = 0
– 16(t + 5)(t – 5) = 0
t = – 5 or 5
For this context, it will take 5 seconds for the higher climber’s rock to hit the ground.
h2 (t) = – 16(t – 1)2 + 300 = 0
The standard form for this equation is h2 (t) = – 16t2 + 32t + 284, which is not factorable. We will solve from the completed – square form.
– 16(t – 1)2 + 300 = 0
– 16(t – 1)2 = – 300
(t – 1)2 = \(\frac{300}{16}\) [square root both sides]
t – 1 = ±\(\frac{\sqrt{300}}{4}\)
t = 1±\(\frac{\sqrt{300}}{4}\) ≈ – 3.3 or 5.3
For this context, it will take approximately 5.3 seconds for the lower climber’s rock to hit the ground.
The rock dropped from the higher position will hit the ground approximately 0.3 seconds before the rock dropped from the lower position. (Notice that the first function equation is easy to factor, but the other is not. Students may try to factor but may use the completed – square form to solve or may opt to use the quadratic formula on the second one.)
c. Graph the two functions on the same coordinate plane, and identify the key features that show that your answer to part (b) is correct. Explain how the graphs show that the two rocks hit the ground at different times.
Answer:
The two times are indicated on the x – axis as the x – intercepts. The red graph shows the height – to – time relationship for the rock dropped from 300 ft., and the blue graph shows the same for the rock dropped from 400 ft. For the red graph, h(t) = 0 when t = 5.3, and for the blue graph, h(t) = 0 when t = 5.
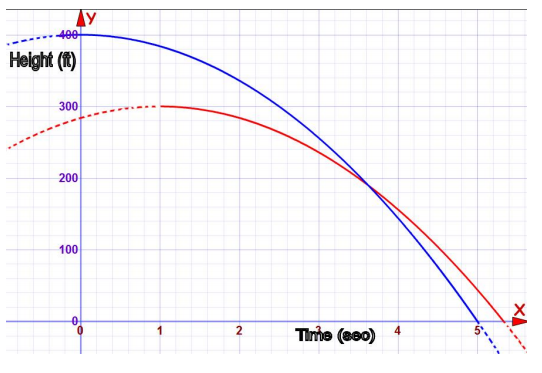
d. Does the graph show how far apart the rocks were when they landed? Explain.
Answer:
No, the graph only shows the height of the rocks with respect to time. Horizontal position and movement are not indicated in the function or the graph.
Exercise 2.
Amazing Photography Studio takes school pictures and charges $20 for each class picture. The company sells an average of 12 class pictures in each classroom. They would like to have a special sale that will help them sell more pictures and actually increase their revenue. They hired a business analyst to determine how to do that. The analyst determined that for every reduction of $2 in the cost of the class picture, there would be an additional 5 pictures sold per classroom.
a. Write a function to represent the revenue for each classroom for the special sale.
Answer:
Let x represent the number of $2 reductions in price.
Then the price expression would be 20 – 2x.
The quantity expression would be 12 + 5x.
So, the revenue is R(x) = (20 – 2x)(12 + 5x) = 240 + 100x – 24x – 10x2 = – 10x2 + 76x + 240.
b. What should the special sale price be?
Answer:
Find the vertex for R(x) = – 10x2 + 76x + 240.
– 10(x2 – 7.6x + ____) + 240
– 10(x2 – 7.6x + 3.82) + 240 + 3.82 (10) = – 10(x – 3.8)2 + 240 + 144.40
So, R(x) = – 10(x – 3.8)2 + 384.4, and the studio should reduce the price by between three or four
$2 – increments.
If we check the revenue amount for 3 reductions, the price is $20 – $2(3) = $14. The quantity will be
12 + 5(3) = 27 pictures per classroom, so the revenue would be $378.
Now check 4 reductions: The price is $20 – $2(4) = $12. The quantity will be 12 + 5(4) = 32 pictures per classroom, and the revenue for 4 reductions would be $384.
The special sale price should be $12 since the revenue was greater than when the price was $14.
c. How much more will the studio make than they would have without the sale?
Answer:
The revenue for each class will be $384 during the sale. Without the sale, they would make $20 per picture for 12 pictures, or $240. They will increase their revenue by $144 per classroom.
Eureka Math Algebra 1 Module 4 Lesson 23 Problem Set Answer Key
Question 1.
Dave throws a ball upward with an initial velocity of 32 ft/s. The ball initially leaves his hand 5 ft. above the ground and eventually falls back to the ground. In parts (a)–(d), you will answer the following questions: What is the maximum height reached by the ball? After how many seconds will the ball reach its maximum height? How long will it take the ball to reach the ground?
a. What units will we be using to solve this problem?
Answer:
Height is measured in feet, time is measured in seconds, and velocity is measured in feet per second.
b. What information from the contextual description do we need to use to write the formula for the function h of the height of the ball versus time? Write the formula for height of the ball in feet, h(t), where t stands for seconds.
Answer:
Gravity: – 32 ft/s2
Initial height (h0): 5 ft. above the ground
Initial velocity (v0): 32 ft/s
Function: h(t) = – 16t2 + 32t + 5
c. What is the maximum point reached by the ball? After how many seconds will it reach that height? Show your reasoning.
Answer:
Complete the square:
h(t) = – 16t2 + 32t + 5
h(t) = – 16(t2 – 2t + ▭) + 5 + ▭
h(t) = – 16(t2 – 2t + 1) + 5 + 16 Completing the square
h(t) = – 16(t – 1)2 + 21 The vertex (maximum height) is 21 ft. and is reached at 1 sec.
d. How long will it take for the ball to land on the ground after being thrown? Show your work.
Answer:
The ball will land at a time t when h(t) = 0, that is, when 0 = – 16t2 + 32t + 5:
0 = – 16(t2 – 2t – \(\frac{5}{16}\))
t = \(\frac{ – b \pm \sqrt{b^{2} – 4 a c}}{2 a}\)
t = \(\frac{ – ( – 2) \pm \sqrt{( – 2)^{2} – 4(1)\left( – \frac{5}{16}\right)}}{2(1)}\)
t = \(\frac{2 \pm \sqrt{4 + \frac{20}{16}}}{2}\)
t = \(\frac{2 \pm \sqrt{\frac{21}{4}}}{2}\)
t = 1±\(\frac{\sqrt{21}}{4}\)
t ≈ 2.146 and t ≈ – 0.146
The negative value does not make sense in the context of the problem, so the ball reaches the ground in approximately 2.1 sec.
e. Graph the function of the height of the ball in feet to the time in seconds. Include and label key features of the graph such as the vertex, axis of symmetry, and t – and y – intercepts.
Answer:
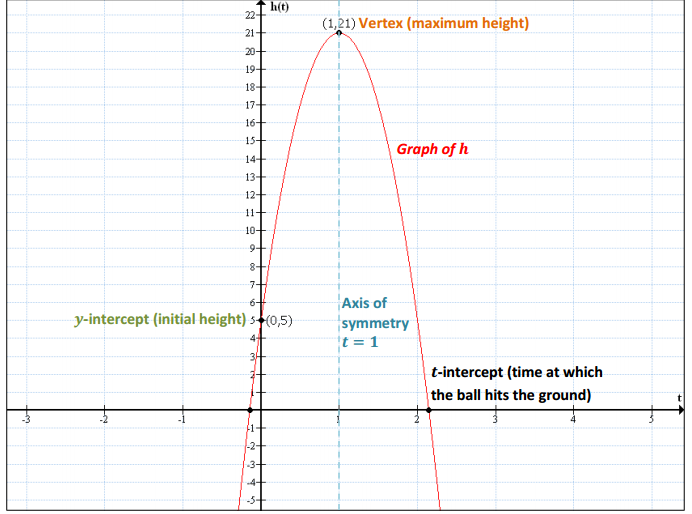
Question 2.
Katrina developed an app that she sells for $5 per download. She has free space on a website that will let her sell 500 downloads. According to some research she did, for each $1 increase in download price, 10 fewer apps are sold. Determine the price that will maximize her profit.
Answer:
Profit equals total revenue minus total production costs. Since the website that Katrina is using allows up to 500 downloads for free, there is no production cost involved, so the total revenue is the total profit.
Let x represent the number of $1 increases to the cost of a download.
Cost per download: 5 + 1x
Apps sold: 500 – 10x
Revenue = (unit price)(quantity sold)
R(x) = (5 + 1x)(500 – 10x)
0 = (5 + 1x)(500 – 10x)
0 = 5 + x or 0 = 500 – 10x
x = – 5 or x = 50
The average of the zeros represents the axis of symmetry.
\(\frac{ – 5 + 50}{2}\) = 22.5 Katrina should raise the cost by $22.50 to earn the greatest revenue.
R(x) = (5 + x)(500 – 10x)
R(x) = – 10x2 + 450x + 2500 Written in standard form
R(22.5) = – 10(22.5)2 + 450(22.5) + 2500
R(22.5) = 7562.50
Katrina will maximize her profit if she increases the price per download by $22.50 to $27.50 per download. Her total revenue (and profit) would be $7,562.50.
Question 3.
Edward is drawing rectangles such that the sum of the length and width is always six inches.
a. Draw one of Edward’s rectangles, and label the length and width.
Answer:

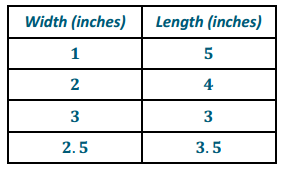
b. Fill in the following table with four different possible lengths and widths.
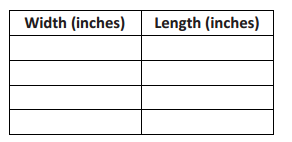
Answer:
c. Let x be the width. Write an expression to represent the length of one of Edward’s rectangles.
Answer:
If x represents the width, then the length of the rectangle would be 6 – x.
d. Write an equation that gives the area, y, in terms of the width, x.
Answer:
Area = length × width
y = x(6 – x)
e. For what width and length will the rectangle have maximum area?
Answer:
y = x(6 – x)
y = – x2 + 6x
y = – 1(x2 – 6x + ▭) + ▭
y = – 1(x2 – 6x + 9) + 9 By completing the square
y = – 1(x – 3)2 + 9 The vertex is (3,9).
The rectangle with the maximum area has a width of 3 in. (also length 3 in.) and an area of 9 in2.
f. Are you surprised by the answer to part (e)? What special name is given for the rectangle in your answer to part (e)?
Answer:
Responses will vary. The special rectangle in part (e) is a square.
Eureka Math Algebra 1 Module 4 Lesson 23 Exit Ticket Answer Key
Question 1.
What is the relevance of the vertex in physics and business applications?
Answer:
By finding the vertex, we know the highest or lowest value for the function and also the x – value that gives that minimum or maximum. In physics, that could mean the highest point for an object in motion. In business, that could mean the minimum cost or the maximum profit or revenue.