Engage NY Eureka Math Algebra 1 Module 4 Lesson 14 Answer Key
Eureka Math Algebra 1 Module 4 Lesson 14 Exercise Answer Key
Opening Exercise
a. Solve for x by completing the square: x2 + 2x = 8.
Answer:
To solve by completing the square, factor out the leading coefficient, complete the square, and balance the equality.
(x2 + 2x + ) = 8 +
(x2 + 2x + 1) = 8 + 1
(x + 1)2 = 9
(x + 1) = ±\(\sqrt{9}\)
x = – 1±\(\sqrt{9}\)
x = – 1 + 3 or – 1 – 3
x = 2 or – 4
Note: This equation can also be solved by factoring.
b. Solve for p by completing the square: 7p2 – 12p + 4 = 0.
Answer:
To solve by completing the square, first gather the variable terms to one side of the equation and factor out the leading coefficient.
7p2 – 12p = – 4
7(p2 – \(\frac{12}{7}\) p + (\(\frac{6}{7}\))2 ) = – 4 + \(\frac{7(36)}{49}\)
7(p–\(\frac{6}{7}\))2 = – 4 + 3\(\frac{6}{7}\)
7(p – \(\frac{6}{7}\) )2 = \(\frac{8}{7}\)
(p – \(\frac{6}{7}\) )2 = \(\frac{8}{49}\)
(p – \(\frac{6}{7}\)) = ±\(\frac{\sqrt{8}}{7}\)
p = \(\frac{6}{7}\) ± \(\frac{\sqrt{8}}{7}\) OR approximately 1.26 or 0.45
Discussion
Solve ax2 + bx + c = 0.
Answer:

Exercises 1–4
Use the quadratic formula to solve each equation.
Exercise 1.
x2 – 2x = 12→a = 1, b = – 2, c = – 12 [Watch the negatives.]
Answer:
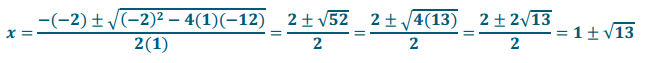
Exercise 2.
\(\sqrt{\frac{1}{9}}\) r2 – 6r = 2→a = \(\frac{1}{2}\), b = – 6, c = – 2 [Did you remember the negative?]
Answer:
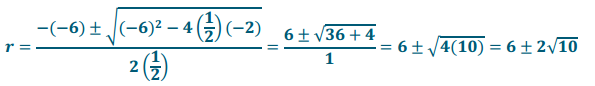
Exercise 3.
2p2 + 8p = 7→a = 2, b = 8, c = – 7
Answer:
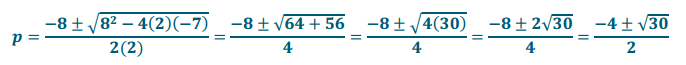
Note: In the Lesson 13 problem, the radical in the final answer was \(\sqrt{\frac{15}{2}}\), which is equivalent to \(\sqrt{\frac{30}{2}}\).
Exercise 4.
2y2 + 3y – 5 = 4→a = 2, b = 3, c = – 9
Answer:
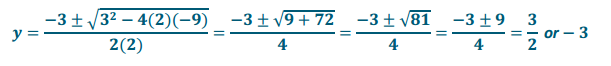
Exercise 5.
Solve these quadratic equations, using a different method for each: solve by factoring, solve by completing the square, and solve using the quadratic formula. Before starting, indicate which method you will use for each.
Method ______________
2x2 + 5x – 3 = 0
Method ______________
x2 + 3x – 5 = 0
Method ______________
\(\frac{1}{2}\) x2 – x – 4 = 0
Answer:
(Students may choose any method to solve. However, the first and third are factorable, but the middle expression is not.)
Method by factoring
2x2 + 5x – 3 = 0
(2x – 1)(x + 3) = 0
x = \(\frac{1}{2}\) or – 3
Method by quadratic formula
x2 + 3x – 5 = 0
x = \(\frac{ – 3 \pm \sqrt{3^{2} – 4(1)( – 5)}}{2(1)}\)
x = \(\frac{ – 3 \pm \sqrt{29}}{2}\)
x = \(\frac{ – 3 + \sqrt{29}}{2}\) or \(\frac{ – 3 – \sqrt{29}}{2}\)
x≈1.19 or – 4.19
Method by completing the square
\(\frac{1}{2}\) x2 – x – 4 = 0
\(\frac{1}{2}\) (x2 – 2x ) = 4
\(\frac{1}{2}\) (x2 – 2x + 1) = 4 + \(\frac{1}{2}\)
\(\frac{1}{2}\) (x – 1)2 = 4.5
(x – 1)2 = 9
(x – 1) = ±3
x = 1±3
x = 4 or – 2
Eureka Math Algebra 1 Module 4 Lesson 14 Problem Set Answer Key
Use the quadratic formula to solve each equation.
Question 1.
Solve for z: z2 – 3z – 8 = 0.
Answer:
a = 1, b = – 3, c = – 8
z = \(\frac{ – ( – 3) \pm \sqrt{( – 3)^{2} – 4(1)( – 8)}}{2(1)}\) = \(\frac{3 \pm \sqrt{41}}{2}\)
Question 2.
Solve for q: 2q2 – 8 = 3q.
Answer:
a = 2, b = – 3, c = – 8
q = \(\frac{ – ( – 3) \pm \sqrt{( – 3)^{2} – 4(2)( – 8)}}{2(2)}\) = \(\frac{3 \pm \sqrt{73}}{4}\)
Question 3.
Solve for m: \(\frac{1}{3}\) m2 + 2m + 8 = 5.
Answer:
a = \(\frac{1}{3}\), b = 2, c = 3
m = \(\frac{ – 2 \pm \sqrt{2^{2} – 4\left(\frac{1}{3}\right)(3)}}{2\left(\frac{1}{3}\right)}\) = \(\frac{ – 2 \pm \sqrt{0}}{\frac{2}{3}}\) = – 3
Eureka Math Algebra 1 Module 4 Lesson 14 Exit Ticket Answer Key
Question 1.
Solve for R using any method. Show your work.
\(\frac{3}{2}\) R2 – 2R = 2
Answer:
Let’s start each method by multiplying both sides of the equation by 2 to eliminate the fraction.
3R2 – 4R = 4
