Eureka Math Algebra 1 Module 4 Lesson 12 Answer Key

Engage NY Eureka Math Algebra 1 Module 4 Lesson 12 Answer Key

Eureka Math Algebra 1 Module 4 Lesson 12 Example Answer Key

Example 1.
Now complete the square for 2x² + 16x + 3.
Answer:
Now that students are comfortable with rewriting expressions by completing the square, we can introduce expressions with leading coefficients other than 1. Start by writing the quadratic expression below on the board or screen. Then, walk students through the process of completing the square.
2x² + 16x + 3
Since students already know how to complete the square when the leading coefficient is 1, one way to deal with the leading coefficient is to group the x – terms and factor out the leading coefficient. Then, they can proceed exactly as they did in the previous lesson. Students should be careful to pay attention to the multiplier on the outside of the parentheses and also to the signs involved.
2(x² + 8x ) + 3
Now complete the square of the quadratic expression in the parentheses, and offset the addition on the outside of the parentheses.
2(x² + 8x + 4² ) + 3 – 2(4²)
Make sure all agree that the two operations will reverse each other and that the new expression is equivalent to the old.
2(x + 4)² + 3 – 32 → 2(x + 4)² – 29
Check:
2(x + 4)² – 29=2(x² + 8x + 16) – 29=2x² + 16x + 32 – 29=2x² + 16x + 3
Yes, this matches our original expression.

Example 2.
Business Application Vocabulary
UNIT PRICE (PRICE PER UNIT): The price per item a business sets to sell its product, which is sometimes represented as a linear expression.
QUANTITY: The number of items sold, sometimes represented as a linear expression.
REVENUE: The total income based on sales (but without considering the cost of doing business).
UNIT COST (COST PER UNIT) OR PRODUCTION COST: The cost of producing one item, sometimes represented as a linear expression.
PROFIT: The amount of money a business makes on the sale of its product. Profit is determined by taking the total revenue (the quantity sold multiplied by the price per unit) and subtracting the total cost to produce the items (the quantity sold multiplied by the production cost per unit): Profit=Total Revenue – Total Production Costs.
Answer:
We can integrate the linear relationship of selling price to quantity and the profit formula to create a quadratic equation, which we can then maximize.

The following business formulas are used in this and the remaining lessons in the module:
Total Production Costs=(cost per unit)(quantity of items sold)
Total Revenue=(price per unit)(quantity of items sold)
Profit=Total Revenue – Total Production Costs
Now solve the following problem:
A certain business is marketing its product and has collected data on sales and prices for the past few years. The company determined that when it raised the selling price of the product, the number of sales went down. The cost of producing a single item is $10.
a. Using the data the company collected in this table, determine a linear expression to represent the quantity sold, q.

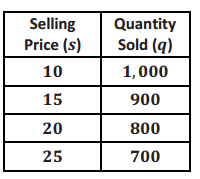
Answer:
q= – 20s + 1200
Use any two of the points of the data to find the slope of the linear relationship, as found in the data, to be – 20. Substitute the coordinates of any (s,q) ordered pair from the table into the equation q= – 20s + b, and solve for b to find the y – intercept, which is 1,200.

Or use a graphic method to find the linear equation. Plot the data on a coordinate plane with s on the horizontal axis and q on the vertical axis. Use any two known points to determine the slope to be – 20.
The y – intercept will be visible, but students should use an algebraic method to verify rather than just estimate from the graph. Substitute these values into slope – intercept form, y=mx + b.

b. Now find an expression to represent the profit function, P.
Answer:
Let q represent the quantity sold, s represent the selling price, and P represent the total profit. The expression P(s) represents the total profit with respect to the selling price.
P=(s)(q) – 10q
The profit formula is
P=Total Revenue – Production Costs, where
Total Revenue=price∙quantity sold and
Production Costs=cost per item∙quantity sold.

P(s)=s( – 20s + 1200) – 10( – 20s + 1200) Substitute – 20s + 1200 for q in the profit formula. (Note that if we factor the common factor from this form of P(s), we get P(s)=( – 20 + 1200)(s – 10). This could save time later when we need to factor.)

P(s)= – 20s² + 1200s + 200s – 12 000 Multiply the expressions, and combine like terms. We now have a quadratic function relating the price per item, s, to profit, P.

P(s)= – 20s² + 1400s – 12 000 This is the expression that represents the profit function.

Eureka Math Algebra 1 Module 4 Lesson 12 Exercise Answer Key

Opening Exercise
Rewrite each expression by completing the square.
a. z² – 5z + 8
Answer:
(z – \(\frac{5}{2}\))² + \(\frac{7}{4}\) OR (z – 2.5)² + 1.75

b. x² + 0.6x + 1
Answer:
(x + 0.3)² + 0.91

Exercises
For Exercises 1–5, rewrite each expression by completing the square.
Exercise 1.
3x² + 12x – 8
Answer:
3(x² + 4x) – 8 → 3(x + 2)² – 8 – 12 → 3(x + 2)² – 20

Exercise 2.
4p² – 12p + 13
Answer:
4(p² – 3p) + 13 → 4(p – \(\frac{3}{2}\))² + 13 – 9 → 4(p – \(\frac{3}{2}\))² + 4

Exercise 3.
\(\frac{1}{2}\) y² + 3y – 4
Answer:
\(\frac{1}{2}\) (y² + 6y) – 4 → \(\frac{1}{2}\) (y + 3)² – 4 – \(\frac{9}{2}\) → \(\frac{1}{2}\) (y + 3)² – \(\frac{17}{2}\)

Exercise 4.
1.2n² – 3n + 6.5
Answer:
1.2(n² – 2.5n) + 6.5 → 1.2(n – 1.25)² + 6.5 – 1.875 → 1.2(n – 1.25)² + 4.625

Exercise 5.
\(\frac{1}{3}\) v² – 4v + 10
\(\frac{1}{3}\) (v² – 12v) + 10 → \(\frac{1}{3}\) (v – 6)² + 10 – 12 → \(\frac{1}{3}\) (v – 6)² – 2

Exercise 6.
A fast food restaurant has determined that its price function is 3 – x/(20 000), where x represents the number of hamburgers sold.
a. The cost of producing x hamburgers is determined by the expression 5000 + 0.56x. Write an expression representing the profit for selling x hamburgers.
Answer:
Profit=Total Revenue – Total Production Costs=(quantity)(price) – cost
=(x)(3 – \(\frac{x}{20000}\)) – (5000 + 0.56x)
=3x – \(\frac{x^{2}}{20000}\) – 5000 – 0.56x
= – \(\frac{x^{2}}{20000}\) + 2.44x – 5000

b. Complete the square for your expression in part (a) to determine the number of hamburgers that need to be sold to maximize the profit, given this price function.
Answer:
– \(\frac{1}{20000}\)(x² – 48 800x + ) – 5000=\(\frac{1}{20000}\) (x² – 48 800x + 24 400² ) – 5000 + \(\frac{24400^{2}}{20000}\)
=\(\frac{1}{20000}\) (x – 24 400)² – 5000 + 29 768
=\(\frac{1}{20000}\) (x – 24 400)² + 24 768
So, 24,400 hamburgers must be sold to maximize the profit using this price expression. Note: The profit will be $24,768.

Eureka Math Algebra 1 Module 4 Lesson 12 Problem Set Answer Key

Question 1.
– 2x² + 8x + 5
Answer:
– 2(x² – 4x + 4) + 5 + 8 → – 2(x – 2)² + 13

Question 2.
2.5k² – 7.5k + 1.25
Answer:
2.5(k² – 3k + 2.25) + 1.25 – 5.625 → 2.5(k – 1.5)² – 4.375

Question 3.
\(\frac{4}{3}\) b² + 6b – 5
Answer:
\(\frac{4}{3}\) (b² + \(\frac{9}{2}\) b + \(\frac{81}{16}\)) – 5 – \(\frac{27}{4}\) → \(\frac{4}{3}\) (b + \(\frac{9}{4}\))² – \(\frac{47}{4}\)

Question 4.
1000c² – 1250c + 695
Answer:
1000(c² – 1.25c + 0.625² ) + 695 – 390.625 → 1000(c – 0.625)² + 304.375

Question 5.
8n² + 2n + 5
Answer:
8(n² + \(\frac{1}{4}\) n + \(\frac{1}{64}\)) + 5 – \(\frac{1}{8}\) → 8(n + \(\frac{1}{8}\))² + 4 \(\frac{7}{8}\)

Eureka Math Algebra 1 Module 4 Lesson 12 Exit Ticket Answer Key

Question 1.
Complete the square: ax² + x + 3.
Answer:
a(x² + \(\frac{1}{a}\) x) + 3 → a(x + \(\frac{1}{2a}\))² + 3 – \(\frac{1}{4a}\)

Question 2.
Write the expression for the profit, P, in terms of q, the quantity sold, and s, the selling price, based on the data collected below on sales and prices. Use the examples and your notes from class to then determine the function that represents yearly profit, P, in terms of the sales, s, given the production cost per item is $30.

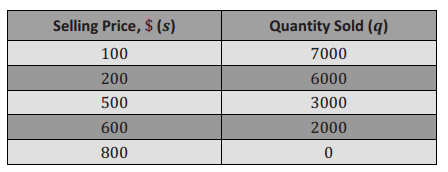
Answer:
The revenue (total income from sales) is the price per item times number of items, (s)(q), and the cost is 30q, so the profit is P = (s)(q) – 30q.
The graph showing the relationship between s and q is a line with slope – 10 and q – intercept 8,000, so
q = – 10s + 8000.
This means the profit function is P(s) = s( – 10s + 8000) – 30( – 10s + 8000).
Factoring the common factors out gives us P(s) = ( – 10s + 8000)(s – 30)= – 10(s – 800)(s – 30).
Or, multiplying and combining like terms gives us P(s) = – 10s² + 8300s – 240 000.