Engage NY Eureka Math Algebra 1 Module 3 Lesson 8 Answer Key
Eureka Math Algebra 1 Module 3 Lesson 8 Exercise Answer Key
Opening Exercise
The sequence of perfect squares {1, 4, 9, 16, 25,…} earned its name because the ancient Greeks realized these quantities could be arranged to form square shapes.

If S(n) denotes the nth square number, what is a formula for S(n)?
Answer:
S(n) = n2
Exercises 1–11
Exercise 1.
Prove whether or not 169 is a perfect square.
Answer:
169 is a perfect square because it can be arranged into a 13 row by 13 column array of dots.
Exercise 2.
Prove whether or not 200 is a perfect square.
Answer:
If 200 is a perfect square, then there is a positive integer a such that a2 = 200. But since 142 = 196, and
152 = 225, we have 14 < a < 15, which means a cannot be an integer.
Hence, 200 is not a perfect square because it cannot be arranged into an n row by n column array of dots.
Exercise 3.
If S(n) = 225, then what is n?
Answer:
n = 15 because 15 × 15 = 225.
Exercise 4.
Which term is the number 400 in the sequence of perfect squares? How do you know?
Answer:
Since 400 = 20 × 20, this number would be the 20th term in the sequence.
Instead of arranging dots into squares, suppose we extend our thinking to consider squares of side length x cm.
Exercise 5.
Create a formula for the area A(x) cm2 of a square of side length x cm: A(x) = ___________.
Answer:
A(x) = x2
Exercise 6.
Use the formula to determine the area of squares with side lengths of 3 cm, 10.5 cm, and π cm.
Answer:
A(3) = 9 The area of a square with side lengths of 3 cm is 9 cm2.
A(10.5) = 110.25 The area of a square with side lengths of 10.5 cm is 0.25 cm2.
A(π) = π2 The area of a square with side lengths of π cm is π2 cm2.
Exercise 7.
What does A(0) mean?
Answer:
In this situation, A(0) has no physical meaning since you cannot have a square whose sides measure cm.
Exercise 8.
What does A( – 10) and A(\(\sqrt{2}\)) mean?
Answer:
In this situation, A( – 10) has no physical meaning since a square cannot have sides whose measure is negative. A(\(\sqrt{2}\)) does have meaning although it would be impossible to measure that side length physically with a ruler.
The only way for the input to be negative is if we redefine what the input value represents—perhaps we just want to find the square of a number and not relate it to a geometric figure at all.
The triangular numbers are the numbers that arise from arranging dots into triangular figures as shown:

Exercise 9.
What is the 100th triangular number?
Answer:
It would be 100(101) divided by 2 or 5050 using the idea displayed in the picture in Exercise 12 below.
Exercise 10.
Find a formula for T(n), the nth triangular number (starting with n = 1).
Answer:
T(n) = \(\frac{n(n + 1)}{2}\)
Exercise 11.
How can you be sure your formula works?
Answer:
By substituting a term number into the formula, you get the correct number of dots in that figure. The formula also works because each triangular number is exactly half of a rectangular arrangement of dots whose dimensions are n by n + 1. For example:

Exercises 12–14
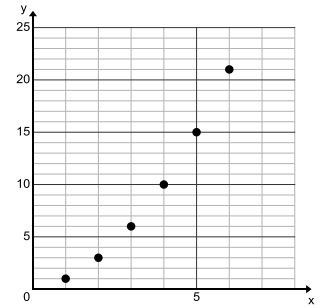
Exercise 12.
Create a graph of the sequence of triangular numbers T(n) = \(\frac{n(n + 1)}{2}\), where n is a positive integer.
Answer:
Exercise 13.
Create a graph of the triangle area formula T(x) = \(\frac{x(x + 1)}{2}\), where x is any positive real number.
Answer:
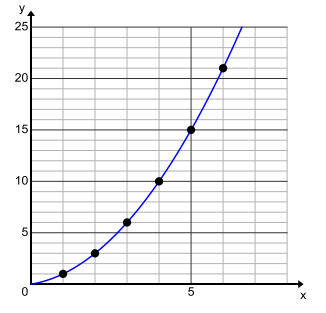
Exercise 14.
How are your two graphs alike? How are they different?
Answer:
The graph of Exercise 12 is not connected because the input values must be positive integers.
The graph of Exercise 13 is connected because the area of a triangle can be any positive real number. Both graphs have points in common at the positive integer input values. Neither graph is a linear or an exponential function.
Eureka Math Algebra 1 Module 3 Lesson 8 Problem Set Answer Key
Question 1.
The first four terms of two different sequences are shown below. Sequence A is given in the table, and sequence B is graphed as a set of ordered pairs.
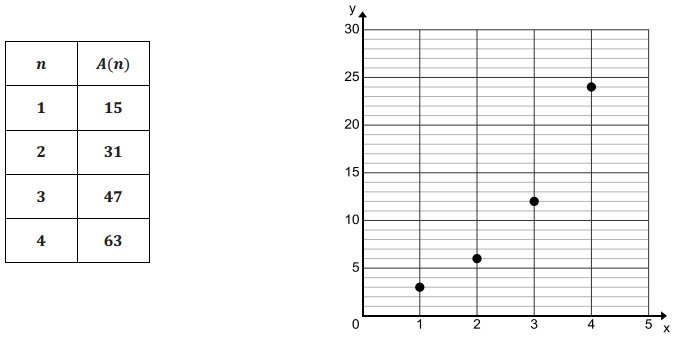
a. Create an explicit formula for each sequence.
Answer:
A(n) = 15 + 16(n – 1), where n is an integer greater than 0. B(n) = 3(2)(n – 1), where n is an integer greater than 0.
b. Which sequence will be the first to exceed 500? How do you know?
Answer:
Students may use observation of the rate of growth in the table and graph or use the formulas they wrote in part (a) to describe that the growth rate of sequence B will cause it to eventually exceed the values of sequence A and to reach 500 before sequence A does. They may also choose a more definitive proof by extending tables of values or graphs of the terms to see which sequence exceeds 500 first. Alternatively, they could choose to use trial and error or algebra skills to find the smallest value of n for which each formula yields a value of 500 or greater. For sequence A, n = 32 is the first term to yield a value greater than 500. For sequence B, n = 9 is the first term to yield a value greater than 500.
Question 2.
A tile pattern is shown below.
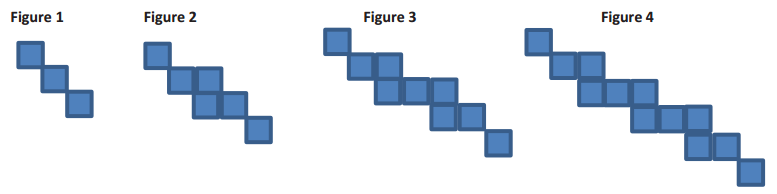
a. How is this pattern growing?
Answer:
Each figure contains three more tiles than the previous figure.
b. Create an explicit formula that could be used to determine the number of squares in the nth figure.
Answer:
F(n) = 3n, where n is a positive integer.
c. Evaluate your formula for n = 0 and n = 2.5. Draw Figure 0 and Figure 2.5, and explain how you decided to create your drawings.
Answer:
F(0) = 0, and F(2.5) = 7.5. You could draw no squares for Figure 0.
You could draw 7 squares and \(\frac{1}{2}\) of a square for Figure 2.5.
Question 3.
The first four terms of a geometric sequence are graphed as a set of ordered pairs.
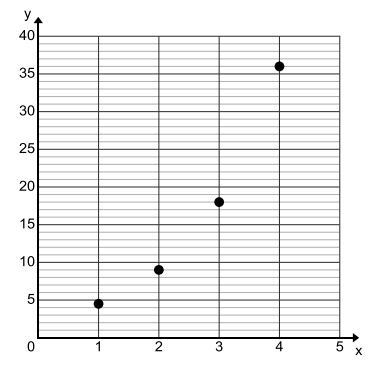
a. What is an explicit formula for this sequence?
Answer:
A(n) = 4.5(2)(n – 1) for n > 0.
b. Explain the meaning of the ordered pair (3,18).
Answer:
It means that the 3rd term in the sequence is 18, or A(3) = 18.
c. As of July 2013, Justin Bieber had over 42,000,000 Twitter followers. Suppose the sequence represents the number of people that follow your new Twitter account each week since you started tweeting. If your followers keep growing in the same manner, when will you exceed 1,000,000 followers?
Answer:
This sequence will exceed 1,000,000 followers when n > 19. At some time in the 19th week, I would have 1,000,000 followers.
Eureka Math Algebra 1 Module 3 Lesson 8 Exit Ticket Answer Key
Recall that an odd number is a number that is one more than or one less than twice an integer. Consider the sequence formed by the odd numbers {1, 3, 5, 7,…}.

Question 1.
Find a formula for O(n), the nth odd number starting with n = 1.
Answer:
O(n) = 2n – 1
Question 2.
Write a convincing argument that 121 is an odd number.
Answer:
121 is an odd number because it can be represented as 2(60) + 1 (one more than twice an integer) or as a column of 60 dots next to a column of 61 dots. Let n = 61. Then O(61) = 2(61) – 1 = 121.
Question 3.
What is the meaning of O(17)?
Answer:
That represents the 17th term of the sequence. That number is 2(17) – 1 or 33.