Eureka Math Algebra 1 Module 3 Lesson 3 Answer Key

Engage NY Eureka Math Algebra 1 Module 3 Lesson 3 Answer Key

Eureka Math Algebra 1 Module 3 Lesson 3 Exercise Answer Key

Exercise 2.
Think of a real – world example of an arithmetic or a geometric sequence. Describe it, and write its formula.
Answer:
Answers will vary. An example of an arithmetic sequence would be a person’s salary that increases by $2,000 each year. A recursive formula would be S(n + 1) = S(n) + 2,000 for n ≥ 1 for some initial salary S(1). An example of a geometric sequence would be a person’s salary that increases by 2% each year. A recursive formula would be
S(n + 1) = 1.02S(n) for n ≥ 1 for some initial salary S(1).

Exercise 3.
If we fold a rectangular piece of paper in half multiple times and count the number of rectangles created, what type of sequence are we creating? Can you write the formula?
Answer:
We are creating a geometric sequence because each time we fold, we double the number of rectangles. R(n) = 2ⁿ, where n is the number of times we have folded the paper.

Eureka Math Algebra 1 Module 3 Lesson 3 Problem Set Answer Key

For Problems 1–4, list the first five terms of each sequence, and identify them as arithmetic or geometric.
Question 1.
A(n + 1) = A(n) + 4 for n ≥ 1 and A(1) = – 2
Answer:
– 2, 2, 6, 10, 14 Arithmetic

Question 2.
A(n + 1) = \(\frac{1}{4}\) ⋅ A(n) for n ≥ 1 and A(1) = 8
Answer:
8, 2, \(\frac{1}{2}\), \(\frac{1}{8}\), \(\frac{1}{32}\) Geometric

Question 3.
A(n + 1) = A(n) – 19 for n ≥ 1 and A(1) = – 6
Answer:
– 6, – 25, – 44, – 63, – 82 Arithmetic

Question 4.
A(n + 1) = \(\frac{2}{3}\) A(n) for n ≥ 1 and A(1) = 6
Answer:
6, 4, \(\frac{8}{3}\), \(\frac{16}{9}\), \(\frac{32}{27}\) Geometric

For Problems 5–8, identify the sequence as arithmetic or geometric, and write a recursive formula for the sequence. Be sure to identify your starting value.
Question 5.
14, 21, 28, 35, …
Answer:
f(n + 1) = f(n) + 7 for n ≥ 1 and f(1) = 14 Arithmetic

Question 6.
4, 40, 400, 4000, …
Answer:
f(n + 1) = 10f(n) for n ≥ 1 and f(1) = 4 Geometric

Question 7.
49, 7, 1, \(\frac{1}{7}\), \(\frac{1}{49}\), …
Answer:
f(n + 1) = \(\frac{1}{7}\)f(n) for n ≥ 1 and f(1) = 49 Geometric

Question 8.
– 101, – 91, – 81, – 71, …
Answer:
f(n + 1) = f(n) + 10 for n ≥ 1 and f(1) = – 101 Arithmetic

Question 9.
The local football team won the championship several years ago, and since then, ticket prices have been increasing $20 per year. The year they won the championship, tickets were $50. Write a recursive formula for a sequence that models ticket prices. Is the sequence arithmetic or geometric?
Answer:
T(n) = 50 + 20n, where n is the number of years since they won the championship; n ≥ 1 (n ≥ 0 is also acceptable). The sequence is arithmetic.
OR
T(n + 1) = T(n) + 20, where n is the number of years since the year they won the championship; n ≥ 1 and T(1) = 70 (n ≥ 0 and T(0) = 50 is also acceptable). The sequence is arithmetic.

Question 10.
A radioactive substance decreases in the amount of grams by one – third each year. If the starting amount of the substance in a rock is 1,452 g, write a recursive formula for a sequence that models the amount of the substance left after the end of each year. Is the sequence arithmetic or geometric?
Answer:
A(n + 1) = \(\frac{2}{3}\) A(n) or A(n + 1) = 2A(n)÷3, where n is the number of years since the measurement started, A(0) = 1,452
The sequence is geometric.
Since the problem asked how much radioactive substance was left, students must take the original amount, divide by 3 or multiply by \(\frac{1}{3}\), and then subtract that portion from the original amount. An easier way to do this is to just multiply by the amount remaining. If \(\frac{1}{3}\) is eliminated, \(\frac{2}{3}\) remains.

Question 11.
Find an explicit form f(n) for each of the following arithmetic sequences (assume a is some real number and x is some real number).
a. – 34, – 22, – 10, 2, …
Answer:
f(n) = – 34 + 12(n – 1) = 12n – 46, where n ≥ 1

b. \(\frac{1}{5}\), \(\frac{1}{10}\), 0, – \(\frac{1}{10}\), …
Answer:
f(n) = \(\frac{1}{5}\) – \(\frac{1}{10}\)(n – 1) = \(\frac{3}{10}\) – \(\frac{1}{10}\)n, where n ≥ 1

c. x + 4, x + 8, x + 12, x + 16, …
Answer:
f(n) = x + 4 + 4(n – 1) = x + 4n, where n ≥ 1

d. a, 2a + 1, 3a + 2, 4a + 3, …
Answer:
f(n) = a + (a + 1)(n – 1) = a + an – a + n – 1 = an + n – 1, where n ≥ 1

Question 12.
Consider the arithmetic sequence 13, 24, 35, ….
a. Find an explicit form for the sequence in terms of n.
Answer:
f(n) = 13 + 11(n – 1) = 11n + 2, where n ≥ 1

b. Find the 40th term.
Answer:
f(40) = 442

c. If the nth term is 299, find the value of n.
Answer:
299 = 11n + 2 → n = 27

Question 13.
If – 2, a, b, c, 14 forms an arithmetic sequence, find the values of a, b, and c.
Answer:
14 = – 2 + (5 – 1)d
16 = 4d
d = 4

a = – 2 + 4 = 2
b = 2 + 4 = 6
c = 6 + 4 = 10

Question 14.
3 + x, 9 + 3x, 13 + 4x, … is an arithmetic sequence for some real number x.
a. Find the value of x.
Answer:
The difference between term 1 and term 2 can be expressed as (9 + 3x) – (3 + x) = 6 + 2x.
The difference between term 2 and term 3 can be expressed as (13 + 4x) – (9 + 3x) = 4 + x.
Since the sequence is known to be arithmetic, the difference between term 1 and term 2 must be equal to the difference between term 2 and term 3. Thus, 6 + 2x = 4 + x, and x = – 2; therefore, the sequence is
1, 3, 5, ….

b. Find the 10th term of the sequence.
Answer:
f(n) = 1 + 2(n – 1) = 2n – 1, where n ≥ 1
f(10) = 19

Question 15.
Find an explicit form f(n) of the arithmetic sequence where the 2nd term is 25 and the sum of the 3rd term and 4th term is 86.
Answer:
a,25,b,c
25 = a + (2 – 1)d
25 = a + d

b = 25 + d
b = a + 2d

c = 25 + 2d
c = a + 3d
b + c = (a + 2d) + (a + 3d) = 2a + 5d = 86
a + d = 25
Solving this system: d = 12, a = 13, so f(n) = 13 + 12(n – 1), where n ≥ 1
b = 13 + 2(12) = 37
c = 13 + 3(12) = 49
OR
b + c = (25 + d) + (25 + 2d) = 50 + 3d = 86 → d = 12
25 = a + 12 → a = 13
b = 25 + 12 → b = 37
c = 25 + 2(12) → c = 49
So, f(n) = 13 + 12(n – 1).

Question 16.
Challenge: In the right triangle figure below, the lengths of the sides a cm, b cm, and c cm of the right triangle form a finite arithmetic sequence. If the perimeter of the triangle is 18 cm, find the values of a, b, and c.

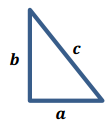
Answer:
a + b + c = 18 b = a + d c = a + 2d
a + (a + d) + (a + 2d) = 18
3a + 3d = 18
a + d = 6 = b
Now, do not forget that it is a right triangle, so the Pythagorean theorem must apply: a² + b² = c².
Since we know that b = 6, the perimeter equation becomes a + c = 12 once b is substituted. So, substituting
c = 12 – a and b into the Pythagorean theorem equation gives us a² + 36 = (12 – a)², which gives us the following answer: a = \(\frac{9}{2}\), b = 6, c = \(\frac{15}{2}\).

Question 17.
Find the common ratio and an explicit form in each of the following geometric sequences.
a. 4, 12, 36, 108, …
Answer:
r = 3 f(n) = 4(3)^{(n – 1)}, where n ≥ 1

b. 162, 108, 72, 48, …
Answer:
r = \(\frac{108}{162}\) = \(\frac{2}{3}\) f(n) = 162(\(\frac{2}{3}\))^{(n – 1)}, where n ≥ 1

c. \(\frac{4}{3}\), \(\frac{2}{3}\), \(\frac{1}{3}\), \(\frac{1}{6}\), …
Answer:
r = \(\frac{1}{2}\) f(n) = (\(\frac{4}{3}\)) (\(\frac{1}{2}\))^{(n – 1)} = (\(\frac{4}{3}\)) (2)^{(1 – n)}, where n ≥ 1

d. xz, x² z³, x³ z⁵, x⁴ z⁷, …
Answer:
r = xz² f(n) = xz(xz² )^{(n – 1)}, where n ≥ 1

Question 18.
The first term in a geometric sequence is 54, and the 5th term is 2/3. Find an explicit form for the geometric sequence.
Answer:
\(\frac{2}{3}\) = 54(r)⁴
\(\frac{1}{81}\) = r⁴
r = \(\frac{1}{3}\) or – \(\frac{1}{3}\)
f(n) = 54(\(\frac{1}{3}\))^{(n – 1)}

Question 19.
If 2, a, b, – 54 forms a geometric sequence, find the values of a and b.
Answer:
a = 2r
b = 2(r)²
– 54 = 2(r)³
– 27 = r³
– 3 = r, so a = – 6 and b = 18

Question 20.
Find the explicit form f(n) of a geometric sequence if f(3) – f(1) = 48 and \(\frac{f(3)}{f(1)}\) = 9.
Answer:
f(3) = f(1) (r)²
\(\frac{f(3)}{f(1)}\) = r² = 9
r = 3 or – 3 f(1) r² – f(1) = 48
f(1)(r² – 1) = 48
f(1)(8) = 48
f(1) = 6
f(n) = 6(3)^{(n – 1)}, where n ≥ 1 or f(n) = 6( – 3)^{(n – 1)}, where n ≥ 1

Eureka Math Algebra 1 Module 3 Lesson 3 Exit Ticket Answer Key

Question 1.
Write the first three terms in the following sequences. Identify them as arithmetic or geometric.
a. A(n + 1) = A(n) – 5 for n ≥ 1 and A(1) = 9
Answer:
9, 4, – 1 Arithmetic

b. A(n + 1) = \(\frac{1}{2}\) A(n) for n ≥ 1 and A(1) = 4
Answer:
4, 2, 1 Geometric

c. A(n + 1) = A(n)÷10 for n ≥ 1 and A(1) = 10
Answer:
10, 1, \(\frac{1}{10}\) or 10, 1, 0.1 Geometric

Question 2.
Identify each sequence as arithmetic or geometric. Explain your answer, and write an explicit formula for the sequence.
a. 14, 11, 8, 5, …
Answer:
Arithmetic
– 3 pattern
17 – 3n, where n starts at 1

b. 2, 10, 50, 250, …
Answer:
Geometric
×5 pattern
2(5^{(n – 1)}), where n starts at 1

c. – \(\frac{1}{2}\), – \(\frac{3}{2}\), – \(\frac{5}{2}\), – \(\frac{7}{2}\), …
Answer:
Arithmetic
– 1 pattern
\(\frac{1}{2}\) – n, where n starts at 1