Engage NY Eureka Math Algebra 1 Module 3 Lesson 24 Answer Key
Eureka Math Algebra 1 Module 3 Lesson 24 Exercise Answer Key
Opening Exercise
Here are two different parking options in the city.

The cost of a 2.75-hour stay at 1-2-3 Parking is $6 + $5 + $4 = $15. The cost of a 2.75-hour stay at Blue Line Parking is $5(2.75) = $13.75.
Which garage costs less for a 5.25-hour stay? Show your work to support your answer.
Answer:
1-2-3 Parking: $6 + $5 + $4(4) = $27
Blue Line Parking: $5(5) + $4(0.25) = $26
Mathematical Modeling Exercise
Helena works as a summer intern at the Albany International Airport. She is studying the parking rates and various parking options. Her department needs to raise parking revenues by 10% to help address increased operating costs. The parking rates as of 2008 are displayed below. Your class will write piecewise linear functions to model each type of rate and then use those functions to develop a plan to increase parking revenues.
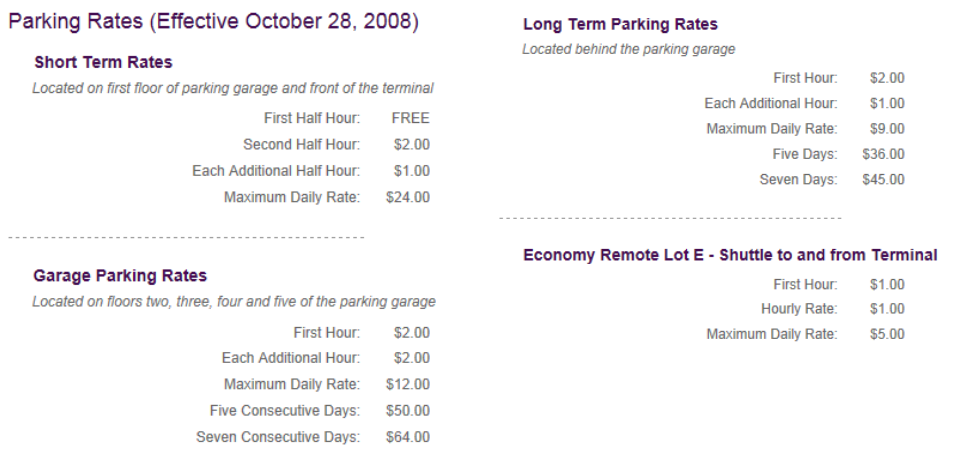
Exercise 1.
Write a piecewise linear function using step functions that models your group’s assigned parking rate. As in the Opening Exercise, assume that if the car is there for any part of the next time period, then that period is counted in full (i.e., 3.75 hours is counted as 4 hours, 3.5 days is counted as 4 days, etc.).
Answer:
Answers may vary. Each function models the parking rate (in dollars) as a function of the number of hours parked.
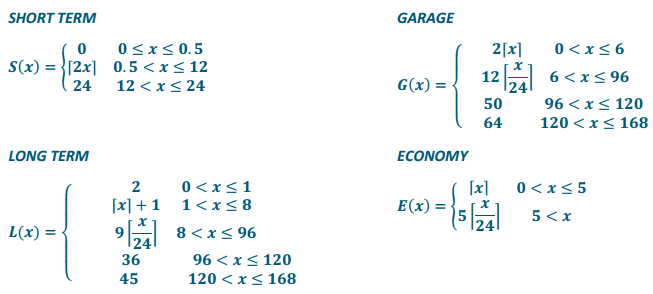
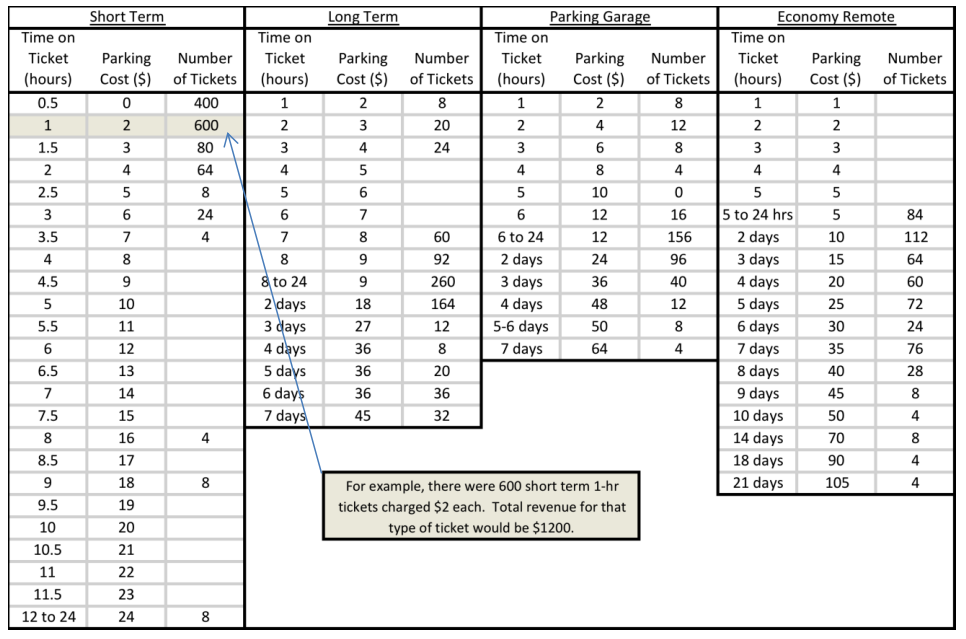
Helena collected all the parking tickets from one day during the summer to help her analyze ways to increase parking revenues and used that data to create the table shown below. The table displays the number of tickets turned in for each time and cost category at the four different parking lots.
Parking Tickets Collected on a Summer Day at the Albany International Airport
Exercise 2.
Compute the total revenue generated by your assigned rate using the given parking ticket data.
Answer:
Total revenue for Short Term: $2, 308
Total revenue for Long Term: $10, 840
Total revenue for Parking Garage: $7, 184
Total revenue for Economy Remote: $11, 900
Total revenue from all lots: $32, 232
Exercise 3.
The Albany International Airport wants to increase the average daily parking revenue by 10%. Make a recommendation to management of one or more parking rates to change to increase daily parking revenue by 10%. Then, use the data Helena collected to show that revenue would increase by 10% if they implement the recommended change.
Answer:
A 10% increase would be a total of $35, 455.20. Student solutions will vary but should be supported with a calculation showing that their changes will result in a 10% increase in parking revenue. The simplest solution would be to raise each rate by 10% across the board. However, consumers may not like the strange-looking parking rates. Another proposal would be to raise short-term rates by $0.50 per half hour and raise economy rates to $6 per day instead of $5.
Eureka Math Algebra 1 Module 3 Lesson 24 Problem Set Answer Key
Question 1.
Recall the parking problem from the Opening Exercise.
a. Write a piecewise linear function P using step functions that models the cost of parking at 1-2-3 Parking for x hours.
Answer:
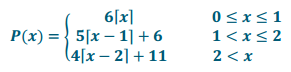
b. Write a piecewise linear function B that models the cost of parking at Blue Line parking for x hours.
Answer:
![]()
c. Evaluate each function at 2.75 and 5.25 hours. Do your answers agree with the work in the Opening Exercise? If not, refine your model.
Answer:
P(2.75) = 15, and B(2.75) = 13.75
P(5.25) = 27, and B(5.25) = 26
d. Is there a time where both models have the same parking cost? Support your reasoning with graphs and/or equations.
Answer:
When x = 5.5, 6.5, 7.5, …
e. Apply your knowledge of transformations to write a new function that would represent the result of a $2 across-the-board increase in hourly rates at 1-2-3 Parking. (Hint: Draw its graph first, and then use the graph to help you determine the step functions and domains.)
Answer:
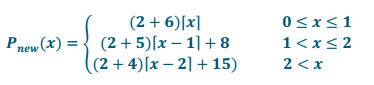
Question 2.
There was no snow on the ground when it started falling at midnight at a constant rate of 1.5 inches per hour. At 4:00 a.m., it starting falling at a constant rate of 3 inches per hour, and then from 7:00 a.m. to 9:00 a.m., snow was falling at a constant rate of 2 inches per hour. It stopped snowing at 9:00 a.m. (Note: This problem models snow falling by a constant rate during each time period. In reality, the snowfall rate might be very close to constant but is unlikely to be perfectly uniform throughout any given time period.)
a. Write a piecewise linear function that models the depth of snow as a function of time since midnight.
Answer:
Let S be a function that gives the depth of snow S(x) on the ground x hours after midnight.
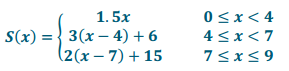
b. Create a graph of the function.
Answer:
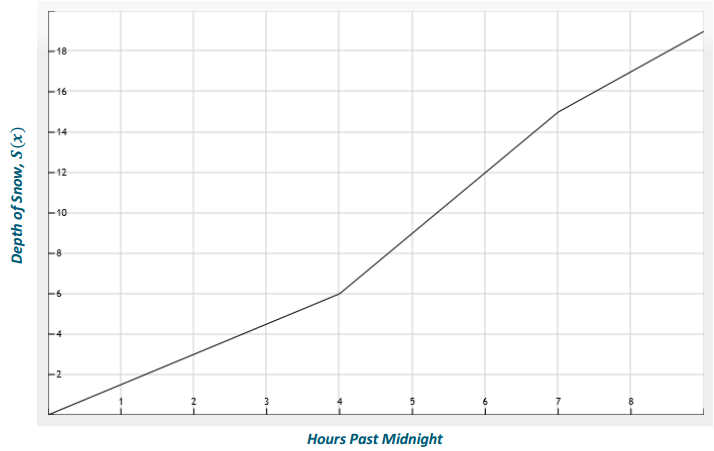
c. When was the depth of the snow on the ground 8 inches?
Answer:
S(x) = 8 when 3(x-4) + 6 = 8
The solution of this equation is x = \(\frac{14}{3}\) hours after midnight or at 4:40 a.m.
d. How deep was the snow at 9:00 a.m.?
Answer:
S(9) = 19 in.
Question 3.
If you earned up to $113, 700 in 2013 from an employer, your social security tax rate was 6.2% of your income. If you earned over $113, 700, you paid a fixed amount of $7, 049.40.
a. Write a piecewise linear function to represent the 2013 social security taxes for incomes between $0 and $500, 000.
Let ![]()
where x is income in dollars and f(x) is the 2013 social security tax.
b. How much social security tax would someone who made $50, 000 owe?
Answer:
f(50000) = 3100; the person would owe $3, 100.
c. How much money would you have made if you paid $4, 000 in social security tax in 2013?
Answer:
f(x) = 4000 when x = 64516.129; you would have made $64, 516.13.
d. What is the meaning of f(150, 000)? What is the value of f(150, 000)?
Answer:
The amount of social security tax you would owe if you earned $150, 000
f(150 000) = $7049.40
Question 4.
The function f gives the cost to ship x lb. via FedEx standard overnight rates to Zone 2 in 2013.
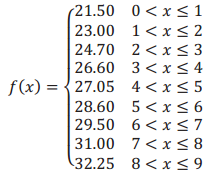
a. How much would it cost to ship a 3 lb. package?
Answer:
f(3) = 24.7; the cost is $24.70.
b. How much would it cost to ship a 7.25 lb. package?
Answer:
f(7.25) = 31; the cost is $31.00.
c. What is the domain and range of f?
Answer:
Domain: x∈(0, 9]
Range: f(x)∈{21.5, 23, 24.7, 26.6, 27.05, 28.6, 29.5, 31, 32.25}
d. Could you use the ceiling function to write this function more concisely? Explain your reasoning.
Answer:
No. The range values on the ceiling function differ by a constant amount. The rates in function f do not increase at a constant rate.
Question 5.
Use the floor or ceiling function and your knowledge of transformations to write a piecewise linear function f whose graph is shown below.
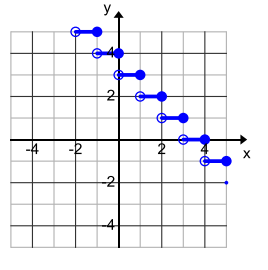
Answer:
f(x) = -⌈x⌉ + 3 or f(x) = ⌊-x⌋ + 4
Eureka Math Algebra 1 Module 3 Lesson 24 Exit Ticket Answer Key
Question 1.
Use the graph to complete the table.
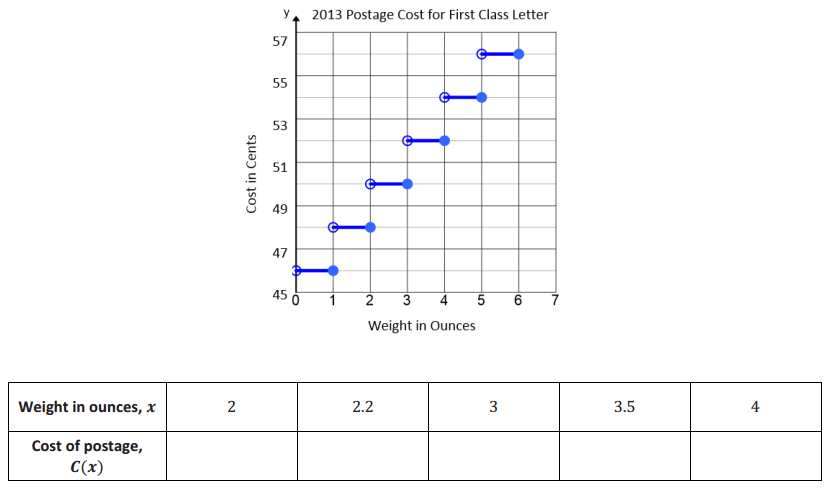
Answer:

Question 2.
Write a formula involving step functions that represents the cost of postage based on the graph shown above.
Answer:
f(x) = 2⌈x⌉ + 44, 0 < x ≤ 6
Question 3.
If it cost Trina $0.54 to mail her letter, how many ounces did it weigh?
Answer:
It weighed more than 4 oz. but less than or equal to 5 oz.