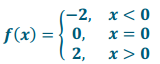Eureka Math Algebra 1 Module 3 Lesson 15 Answer Key

Engage NY Eureka Math Algebra 1 Module 3 Lesson 15 Answer Key

Eureka Math Algebra 1 Module 3 Lesson 15 Exploratory Challenge Answer Key

Exploratory Challenge 1
For parts (a)–(c), create graphs of the solution set of each two – variable equation from Opening Exercise 2.
a. y = |x|

Answer:

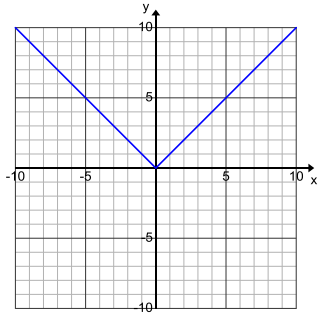
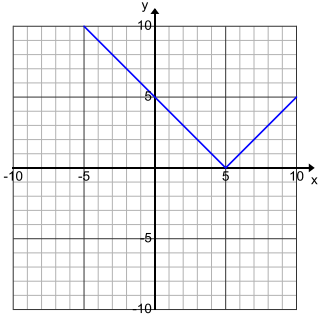
b. y = |x – 5|

Answer:

c. x = |y|

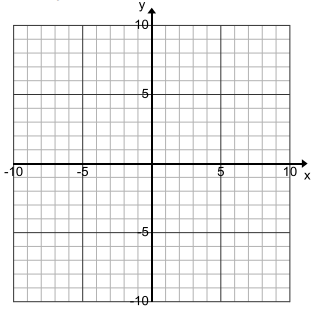
Answer:

d. Write a brief summary comparing and contrasting the three solution sets and their graphs.
Answer:
The graphs of parts (a) and (b) are the same except that part (b) has point of the vee (the vertex of angle) at (5, 0) instead of (0, 0). The graph for part (c) looks like a 90° clockwise rotation of the graph from part (a) about the point (0, 0). The points in the solution sets to parts (a) and (b) are a function, but the points in the solution set for part (c) are not.

For parts (e)–(j), consider the function f(x) = |x|, where x can be any real number.
e. Explain the meaning of the function f in your own words.
Answer:
This function assigns every real number to its absolute value, which is the distance the point is located from 0 on the real number line. Each number and its opposite will have the same range element. The number 0 will be assigned to 0.

f. State the domain and range of this function.
Answer:
Domain: All real numbers
Range: All nonnegative real numbers

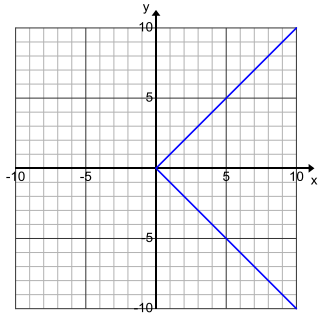
g. Create a graph of the function f. You might start by listing several ordered pairs that represent the corresponding domain and range elements.

Answer:

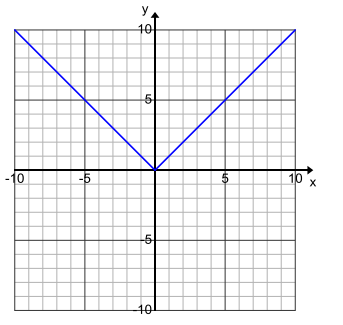
h. How does the graph of the absolute value function compare to the graph of y = |x|?
Answer:
The two graphs are identical. They are identical because each ordered pair in the function would make the equation y = |x| a true number sentence if the domain value were substituted for x, and the range value were substituted for y. Therefore, the graph of the function is the graph of the solution set of the equation.

i. Define a function whose graph would be identical to the graph of y = |x – 5|.
Answer:
Let g(x) = |x – 5|, where x can be any real number.

j. Could you define a function whose graph would be identical to the graph of x = |y|? Explain your reasoning.
Answer:
No. The graph of x = |y| does not meet the definition of a graph of a function. If it were the graph of a function (say, the function h), it would be the set of ordered pairs {(x, h(x)) | x∈D}, which means there would be only one y – value for each x in the domain D. However, in the graph of x = |y| there is a number x (in fact, there are infinitely many x’s) associated with two different y – values. (3, 3) and (3, – 3) are both solutions to the equation x = |y|.

k. Let f₁ (x) = – x for x < 0, and let f₂ (x) = x for ≥ 0 . Graph the functions f₁ and f₂ on the same Cartesian plane. How does the graph of these two functions compare to the graph in part (g)?

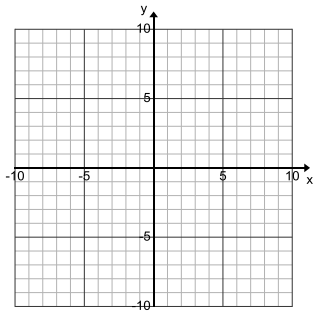
Answer:

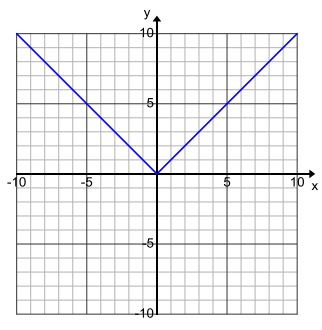
The graph of these two functions when graphed on the same Cartesian plane is identical to the graph of the absolute value function.

Exploratory Challenge 2
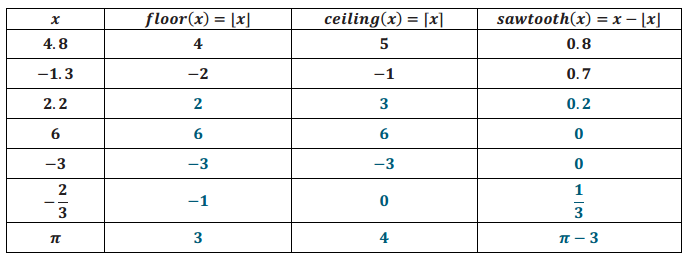
The floor of a real number x, denoted by |x|, is the largest integer not greater than x. The ceiling of a real number x, denoted by |x|, is the smallest integer not less than x. The sawtooth number of a positive number is the fractional part of the number that is to the right of its floor on the number line. In general, for a real number x, the sawtooth number of x is the value of the expression x – |x|. Each of these expressions can be thought of as functions with the domain being the set of real numbers.
a. Complete the following table to help you understand how these functions assign elements of the domain to elements of the range. The first and second rows have been done for you.

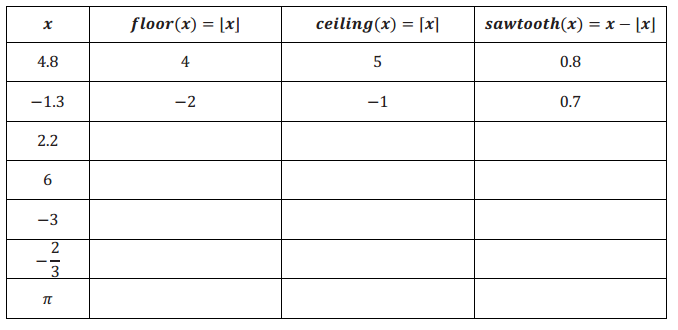
Answer:

b. Create a graph of each function.

Answer:

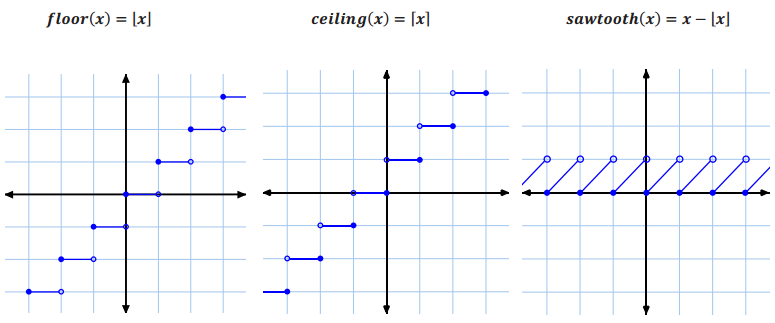
c. For the floor, ceiling, and sawtooth functions, what would be the range values for all real numbers x on the interval [0, 1)? The interval (1, 2]? The interval [ – 2, – 1)? The interval [1.5, 2.5]?
Answer:
Floor: {0}, Ceiling: {0, 1}, Sawtooth: [0, 1).
Floor: {1, 2}, Ceiling: {2}, Sawtooth: [0, 1).
Floor: {–2}, Ceiling: {–2, –1}, Sawtooth: [0, 1).
Floor: {1, 2}, Ceiling: {2, 3}, Sawtooth: [0, 1).

Eureka Math Algebra 1 Module 3 Lesson 15 Example Answer Key

Example 1.
Let g(x) = |x – 5|. The graph of g is the same as the graph of the equation y = |x – 5| you drew in Exploratory Challenge 1, part (b). Use the redrawn graph below to rewrite the function g as a piecewise function.

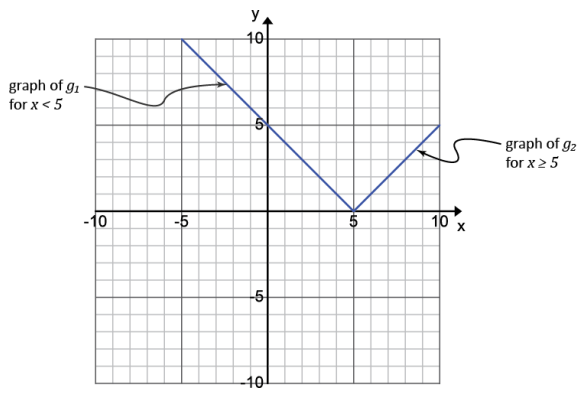
Label the graph of the linear function with negative slope by g₁ and the graph of the linear function with positive slope by g₂, as in the picture above.
Function g₁: The slope of g₁ is – 1 (why?), and the y – intercept is 5; therefore, g₁ (x) = – x + 5.
Function g₂: The slope of g₂ is 1 (why?), and the y – intercept is – 5 (why?); therefore, g₂ (x) = x – 5.
Writing g as a piecewise function is just a matter of collecting all of the different “pieces” and the intervals upon which they are defined:

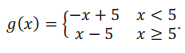
Answer:
→ How does this graph compare to the graph of the translated absolute value function?
→ The graphs are congruent, but the graph of g has been translated to the right 5 units. (Using terms like congruent and translated reinforces concepts from Grade 8 and prepares students for high school Geometry.)
→ How can you use your knowledge of the graph of f(x) = |x| to quickly determine the graph of g(x) = |x – 5|?
→ Watch where the vertex of the graph of f has been translated. In this case, g(x) = |x – 5| has translated the vertex point from (0, 0) to (5, 0). → Then, graph a line with a slope of – 1 for the piece where x < 5 and a line with a slope of 1 for the piece where x > 5.
→ Can we interpret in words what this function does?
→ The range values are found by finding the distance between each domain element and the number 5 on the number line.

Eureka Math Algebra 1 Module 3 Lesson 15 Opening Exercise Answer Key

Opening Exercise
For each real number a, the absolute value of a is the distance between 0 and a on the number line and is denoted |a|.
Question 1.
Solve each one variable equation.
a. |x| = 6
Answer:
{-6, 6}

b. |x – 5| = 4
Answer:
{9, 1}

c. 2|x + 3| = -10
Answer:
No solution.

Question 2.
Determine at least five solutions for each two-variable equation. Make sure some of the solutions include negative values for either x or y.
a. y = |x|
Answer:
{(-2, 2), (-1, 1), (0, 0), (1, 1), (2, 2)}

b. y =|x – 5|
Answer:
{(-1, 6),(0, 5),(1, 4),(5, 0),(6, 1)}

c. x = |y|
Answer:
{(1, 1),(1, -1),(0, 0),(2, 2),(2, -2)}

Eureka Math Algebra 1 Module 3 Lesson 15 Problem Set Answer Key

Question 1.
Explain why the sawtooth function, sawtooth(x) = x – |x| for all real numbers x, takes only the fractional part of a number when the number is positive.
Answer:
If you subtract the integer part of a number from the number, only the fractional par” will remain.

Question 2.
Let g(x) = |x| – |x|, where x can be any real number. In otherwords, g is the difference between the ceiling and floor functions. Express g as a piecewise function.
Answer:

Question 3.
The Heaviside function is defined using the formula below.

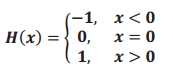
Graph this function, and state its domain and range.
Answer:
Domain: All real numbers
Range: { – 1, 0, 1}

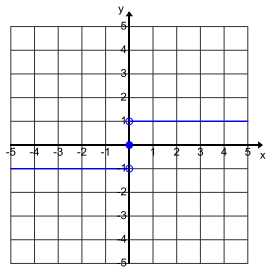
Question 4.
The following piecewise function is an example of a step function.

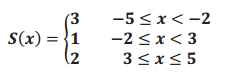
a. Graph this function, and state the domain and range.
Answer:
Domain: [ – 5, 5]
Range: {1, 2, 3}

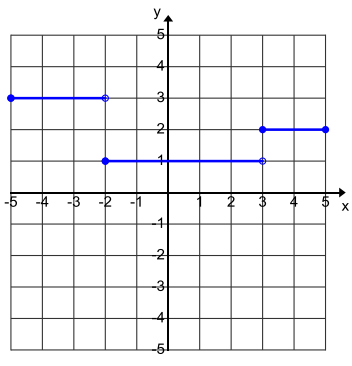
b. Why is this type of function called a step function?
Answer:
The horizontal line segments step up and down like steps.

Question 5.
Let f(x) = \(\frac{|\mathcal{X}|}{\boldsymbol{x}}\), where x can be any real number except 0.
a. Why is the number 0 excluded from the domain of f?
Answer:
If x = 0, then the expression would not be defined.

b. What is the range of f?
Answer:
{ – 1, 1}

c. Create a graph of f.
Answer:

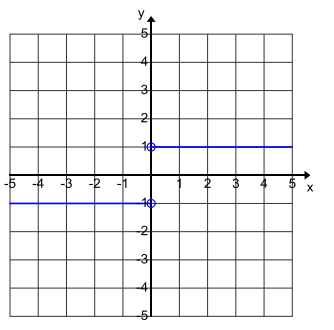
d. Express f as a piecewise function.
Answer:

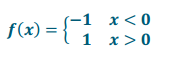
e. What is the difference between this function and the Heaviside function?
Answer:
The domain of the Heaviside function is all real numbers. The Heaviside function has a value of 0 when x = 0. This function excludes the real number 0 from the domain

Question 6.
Graph the following piecewise functions for the specified domain.
a. f(x) = |x + 3| for – 5 ≤ x ≤ 3
Answer:

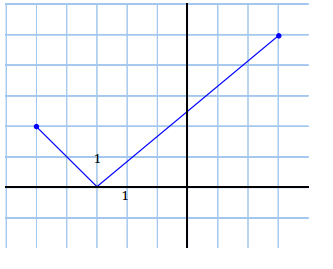
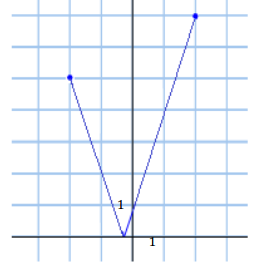
b. f(x) = |2x| for – 3 ≤ x ≤ 3
Answer:

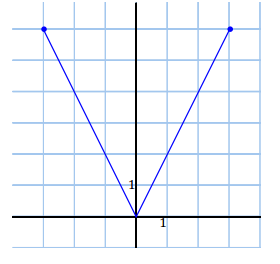
c. f(x) = |2x – 5| for 0 ≤ x ≤ 5
Answer:

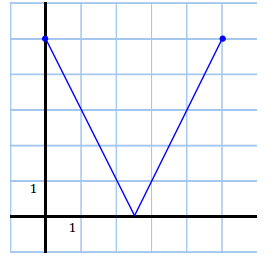
d. f(x) = |3x + 1| for – 2 ≤ x ≤ 2
Answer:

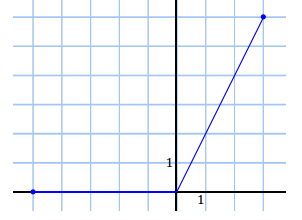
e. f(x) = |x| + x for – 5 ≤ x ≤ 3
Answer:

f.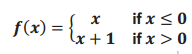
Answer:

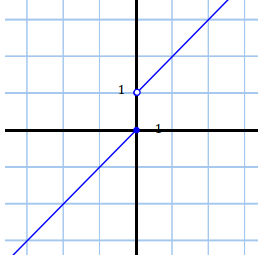
g.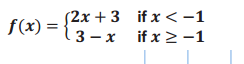
Answer:

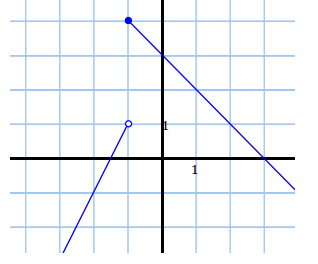
Question 7.
Write a piecewise function for each graph below.
a.

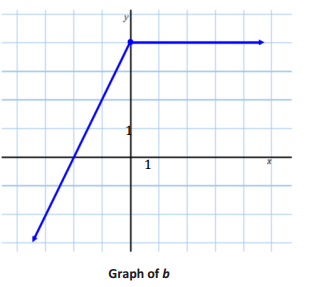
Answer:

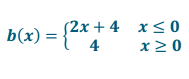
b.

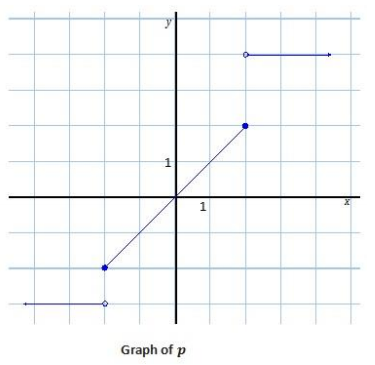
Answer:

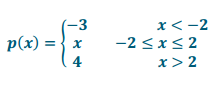
c.

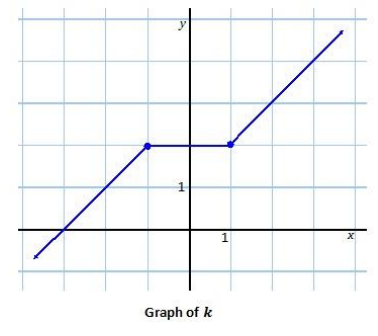
Answer:

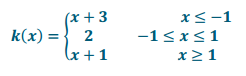
d.

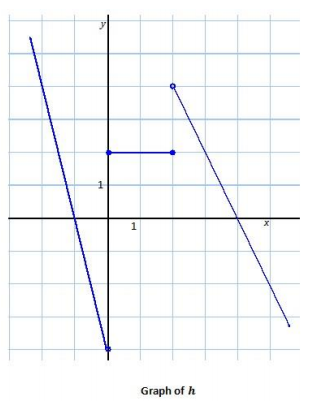
Answer:

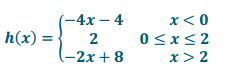
Eureka Math Algebra 1 Module 3 Lesson 15 Exit Ticket Answer Key

Each graph shown below represents the solution set to a two – variable equation.

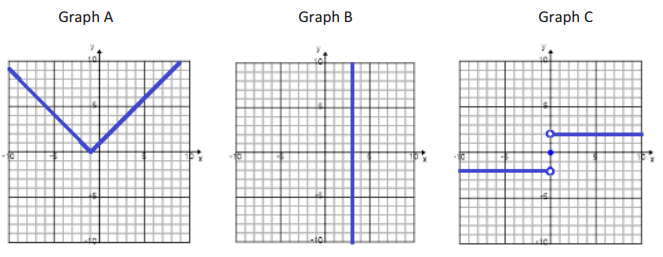
Question 1.
Which of these graphs could be represented by a function? Explain your reasoning.
Answer:
Graphs A and C could be represented by a function because each x in the domain is paired with exactly one y in the range.

Question 2.
For each one that can be represented by a function, define a piecewise function whose graph would be identical to the solution set shown.
Answer:
Graph A: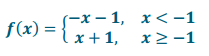
Graph C: