Eureka Math Algebra 1 Module 3 Lesson 12 Answer Key

Engage NY Eureka Math Algebra 1 Module 3 Lesson 12 Answer Key

Eureka Math Algebra 1 Module 3 Lesson 12 Exploratory Challenge Answer Key

Exploratory Challenge 1
Next we write code that generates a graph of a two – variable equation y = x(x – 2)(x + 2) for x in { – 2, – 1, 0, 1, 2} and y in { – 3, 0, 3}. The solution set of this equation is generated by testing each ordered pair (x, y) in the set,
{( – 2, – 3), ( – 2, 0), ( – 2, 3), ( – 1, – 3), ( – 1, 0), ( – 1, 3), …, (2, – 3), (2, 0), (2, 3)},
to see if it is a solution to the equation y = x(x – 2)(x + 2). Then the graph is just the plot of solutions in the Cartesian plane. We can instruct a computer to find these points and plot them using the following program.

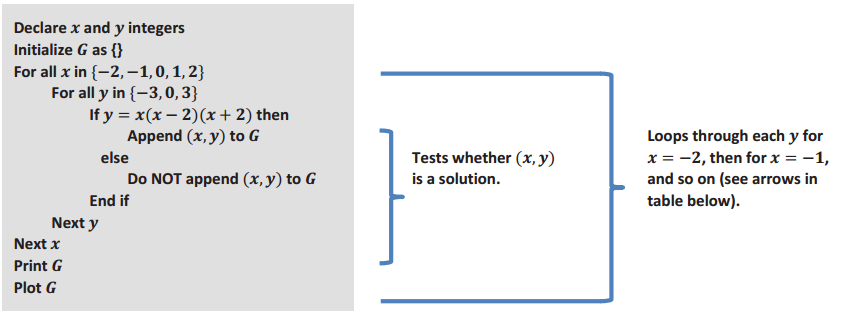
a. Use the table below to record the decisions a computer would make when following the program instructions above. Fill in each cell with “Yes” or “No” depending on whether the ordered pair (x, y) would be appended or not. (The step where x = – 2 has been done for you.)

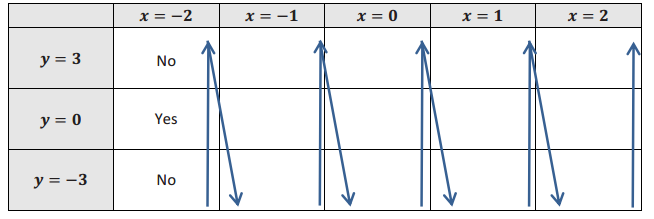
Answer:

b. What would be the output to the Print G command? (The first ordered pair is listed for you.)
Output:
{ ( – 2, 0) , __________, __________, __________, __________ }
Answer:
{ ( – 2, 0), ( – 1, 3), (0, 0), (1, – 3), (2, 0)}

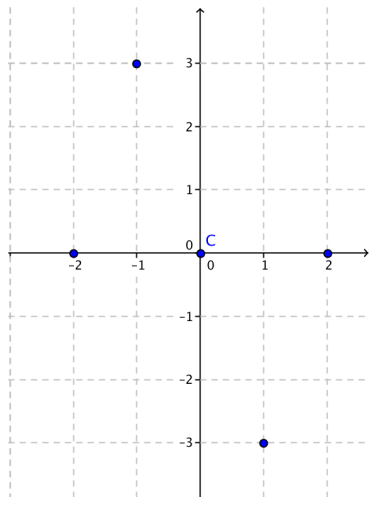
c. Plot the solution set G in the Cartesian plane. (The first ordered pair in G has been plotted for you.)

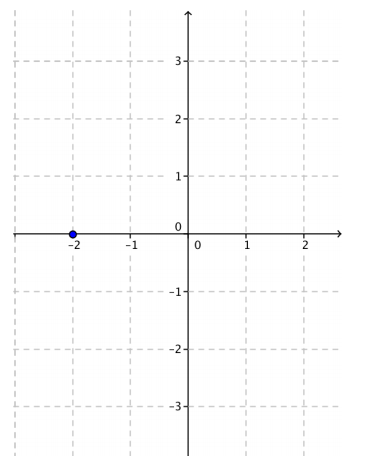
Answer:

Exploratory Challenge 2
The program code in Exercise 3 is a way to imagine how set – builder notation generates solution sets and figures in the plane. Given a function f(x) = x(x – 2)(x – 3) with domain and range all real numbers, a slight modification of the program code above can be used to generate the graph of the equation y = f(x):
{(x, y) | x real and y = f(x)}.
Even though the code below cannot be run on a computer, students can run the following thought code in their minds.

a. Plot G on the Cartesian plane (the figure drawn is called the graph of y = f(x)).

Answer:

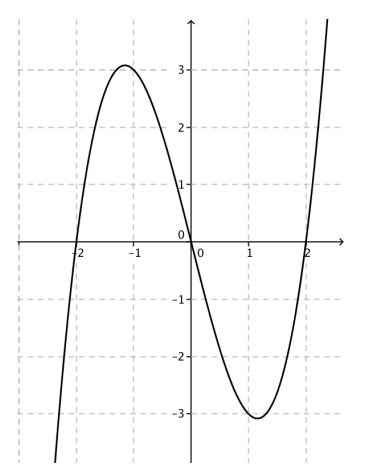
b. Describe how the thought code is similar to the set – builder notation {(x, y) | x real and y = f(x)}.
Answer:
Answer: Both generate sets by checking every point (x, y) in the Cartesian plane, searching for points (x, y) for which the equation y = x(x – 2)(x + 2) is true.

c. A relative maximum for the function f occurs at the x – coordinate of ( – \(\frac{2}{3}\) \(\sqrt{3}\), \(\frac{16}{9}\) \(\sqrt{3}\)). Substitute this point into the equation y = x(x² – 4) to check that it is a solution to y = f(x), and then plot the point on your graph.
Answer:
Check that 16/9 \(\sqrt{3}\) = – \(\frac{2}{3}\) \(\sqrt{3}\) (( – \(\frac{2}{3}\) \(\sqrt{3}\))² – 4) is a true number sentence.
Divide both sides by \(\sqrt{3}\), multiply both sides by \(\frac{9}{2}\) , and evaluate the square to get 8 = – 3(\(\frac{4}{3}\) – 4). Distributing the – 3 shows that ( – \(\frac{2}{3}\) \(\sqrt{3}\), \(\frac{16}{9}\) \(\sqrt{3}\)) is a solution.

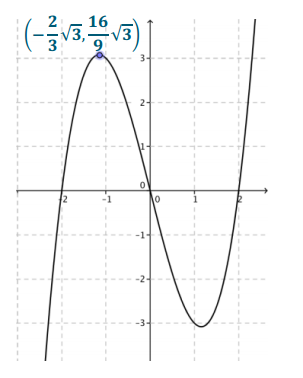
d. A relative minimum for the function f occurs at the x – coordinate of (\(\frac{2}{3}\) \(\sqrt{3}\), – \(\frac{16}{9}\) \(\sqrt{3}\)). A similar calculation as you did above shows that this point is also a solution to y = f(x). Plot this point on your graph.
Answer:
Students should plot the point (\(\frac{2}{3}\) \(\sqrt{3}\), – \(\frac{16}{9}\)9 \(\sqrt{3}\)) on their graphs approximately at (1.15, – 3.08).

e. Look at your graph. On what interval(s) is the function f decreasing?
Answer:
– \(\frac{2}{3}\) \(\sqrt{3}\) ≤ x ≤ \(\frac{2}{3}\) \(\sqrt{3}\) or [ – \(\frac{2}{3}\) \(\sqrt{3}\), \(\frac{2}{3}\) \(\sqrt{3}\)]

f. Look at your graph. On what interval(s) is the function f increasing?
Answer:
x ≤ – \(\frac{2}{3}\) \(\sqrt{3}\) or \(\frac{2}{3}\) \(\sqrt{3}\) ≤ x or ( – ∞, – \(\frac{2}{3}\) \(\sqrt{3}\)] or [\(\frac{2}{3}\) \(\sqrt{3}\), ∞)

Eureka Math Algebra 1 Module 3 Lesson 12 Problem Set Answer Key

Question 1.
Perform the instructions in the following programming code as if you were a computer and your paper were the computer screen.
Declare x integer
For all x from 1 to 6
If x² – 2 = 7 then
Print True
else
Print False
End if
Next x
Answer:
False
False
True
False
False
False

Question 2.
Answer the following questions about the computer programming code.
Declare x integer
Initialize G as { }
For all x from – 3 to 3
If 2^x + 2 ^{– x} = \(\frac{17}{4}\) then
Append x to G
else
Do NOT append x to G
End if
Next x
Print G

a. Perform the instructions in the programming code as if you were a computer and your paper were the computer screen.
Answer:
{ – 2, 2}

b. Write a description of the set G using set – builder notation.
Answer:
{x integer | – 3 ≤ x ≤ 3 and 2^x + 2 ^{– x} = \(\frac{17}{4}\)}

Question 3.
Answer the following questions about the computer programming code.
Declare x and y integers
Initialize G as { }
For all x in {0, 1, 2, 3}
For all y in {0, 1, 2, 3}
If y = \(\sqrt{4 + 20 x – 19 x^{2} + 4 x^{3}}\) then
Append (x, y) to G
else
Do NOT append (x, y) to G
End if
Next y
Next x
Plot G

a. Use the table below to record the decisions a computer would make when following the program instructions above. Fill in each cell with “Yes” or “No” depending on whether the ordered pair (x, y) would be appended or not.

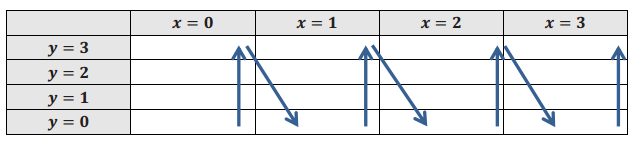
Answer:

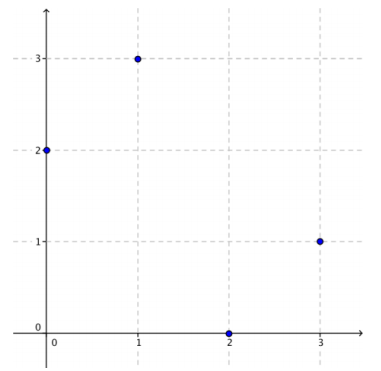
b. Plot the set G in the Cartesian plane.

Answer:

Question 4.
Answer the following questions about the thought code.
Declare x and y real
Let f(x) = – 2x + 8
Initialize G as { }
For all x in the real numbers
For all y in the real numbers
If y = f(x) then
Append (x, y) to G
else
Do NOT append (x, y) to G
End if
Next y
Next x
Plot G

a. What is the domain of the function f(x) = – 2x + 8?
Answer:
All real numbers

b. What is the range of the function f(x) = – 2x + 8?
Answer:
All real numbers

c. Write the set G generated by the thought code in set – builder notation.
Answer:
{(x, y) | y = – 2x + 8}

d. Plot the set G to obtain the graph of the function f(x) = – 2x + 8.
Answer:

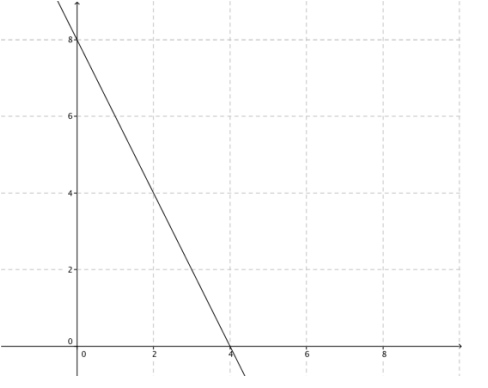
e. The function f(x) = – 2x + 8 is clearly a decreasing function on the domain of the real numbers. Show that the function satisfies the definition of decreasing for the points 8 and 10 on the number line; that is, show that since 8 < 10, then f(8) > f(10).
Answer:
f(8) = – 8 and f(10) = – 12. Since – 8 > – 12, f(8) > f(10).

Question 5.
Sketch the graph of the functions defined by the following formulas, and write the graph of y = f(x) as a set using set – builder notation. (Hint: For each function below, you can assume the domain is all real numbers.)

a. f(x) = – \(\frac{1}{2}\) x + 6
Answer:

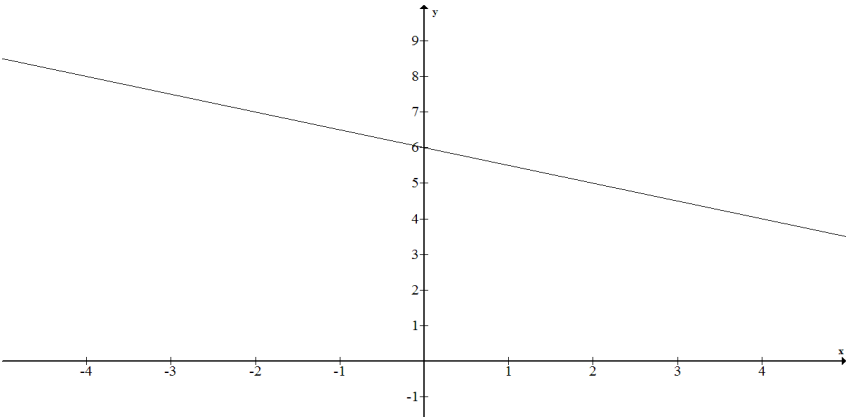
{(x, y) | x real and y = – \(\frac{1}{2}\) x + 6}

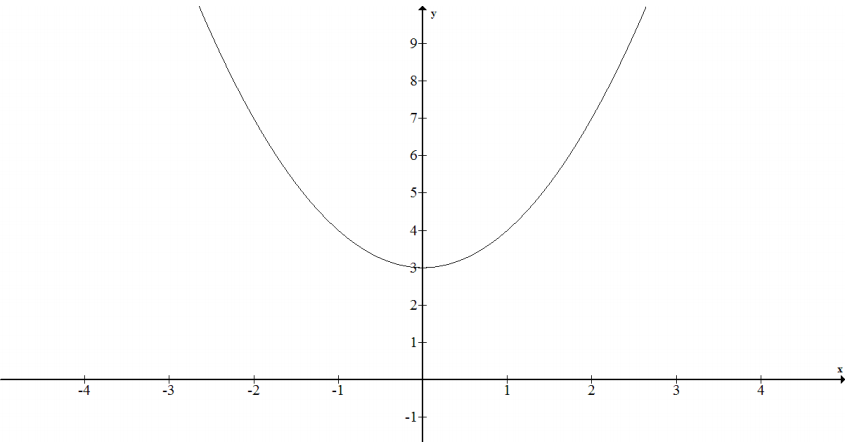
{(x, y) | x real and y = x² + 3}

b. f(x) = x² – 5x + 6
Answer:

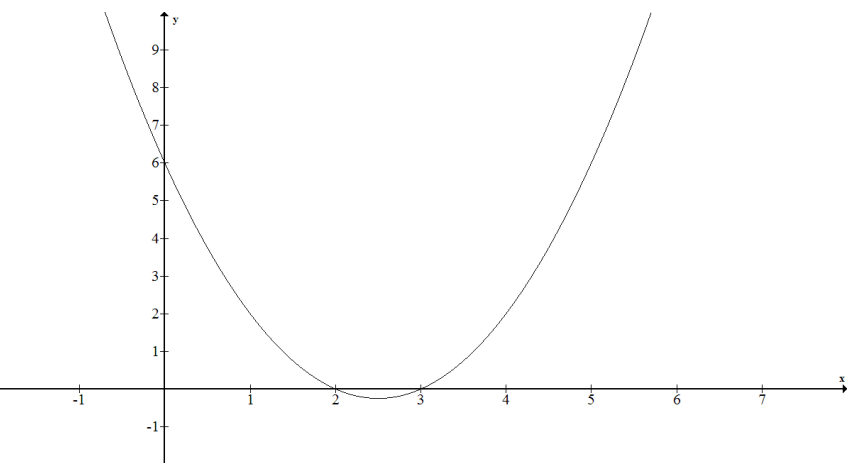
{(x, y) | x real and y = x² – 5x + 6}

c. f(x) = x³ – x
Answer:

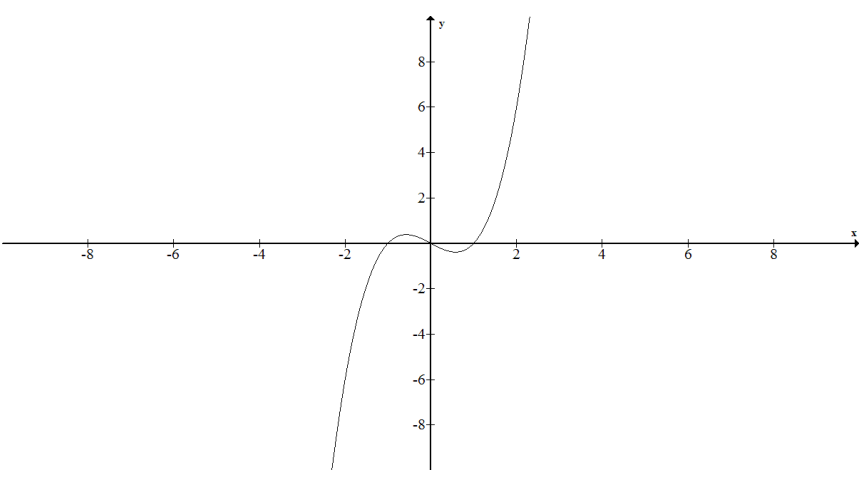
{(x, y) | x real and y = x³ – x}

d. f(x) = – x² + x – 1
Answer:

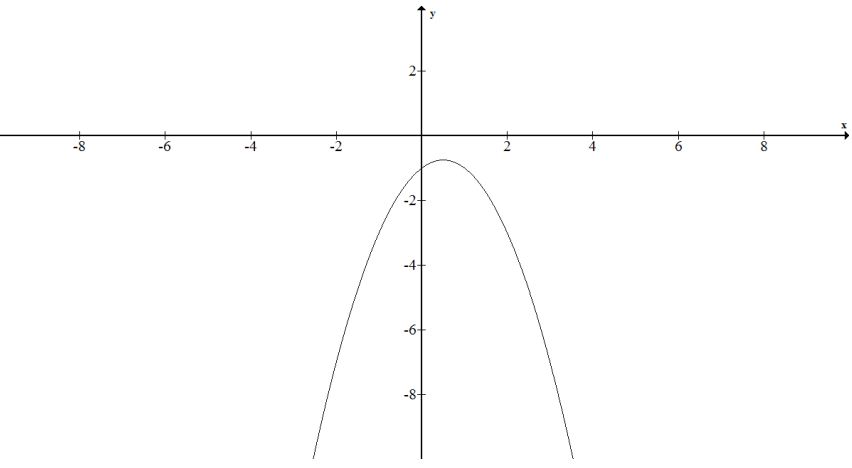
{(x, y) | x real and y = – x² + x – 1}

e. f(x) = (x – 3)² + 2
Answer:

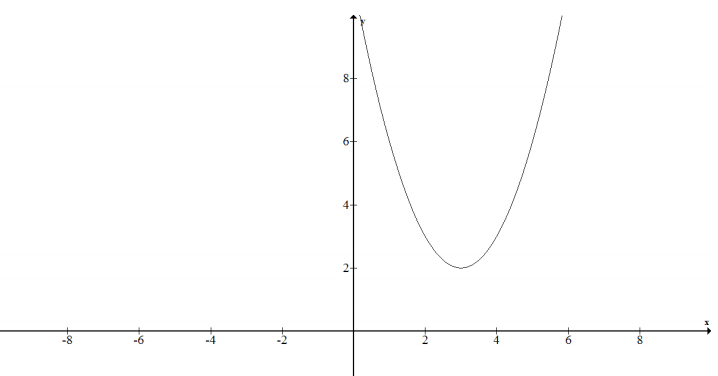
{(x, y) | x real and y = (x – 3)² + 2}

f. f(x) = x³ – 2x² + 3
Answer:

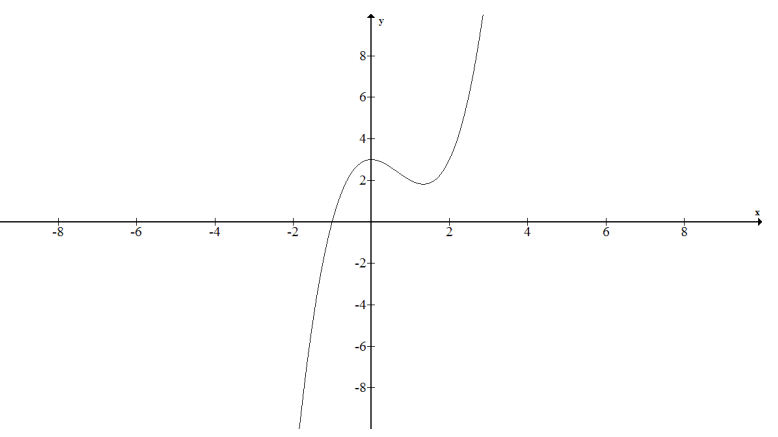
{(x, y) | x real and y = x³ – 2x² + 3}

Question 6.
Answer the following questions about the set:
{(x, y) | 0 ≤ x ≤ 2 and y = 9 – 4x²}.

a. The equation can be rewritten in the form y = f(x) where f(x) = 9 – 4x². What are the domain and range of the function f specified by the set?
i. Domain:
Answer:
0 ≤ x ≤ 2

ii. Range:
Answer:
– 7 ≤ y ≤ 9 or – 7 ≤ f(x) ≤ 9 for x in the domain

b. Write thought code such as that in Problem 4 that will generate and then plot the set.
Answer:
Declare x and y real
Let f(x) = 9 – 4x²
Initialize G as { }
For all x such that 0 ≤ x ≤ 2
For all y such that – 7 ≤ y ≤ 9
If y = f(x) then
Append (x, y) to G
else
Do NOT append (x, y) to G
End if
Next y
Next x
Plot G

Question 7.
Answer the following about the graph of a function below.

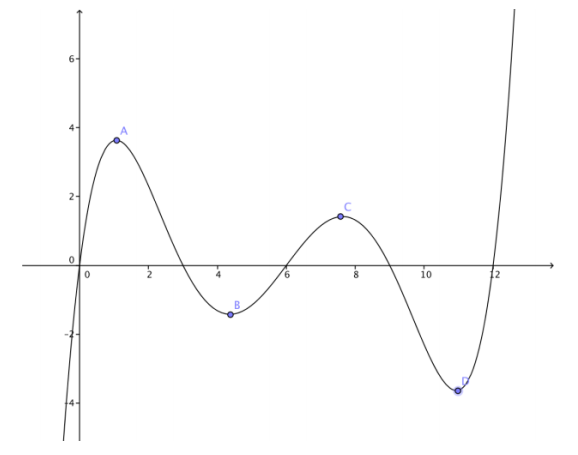
a. Which points (A, B, C, or D) are relative maxima?
Answer:
A and C

b. Which points (A, B, C or D) are relative minima?
Answer:
B and D

c. Name any interval where the function is increasing.
Answer:
Answers may vary. Example: [5, 7]

d. Name any interval where the function is decreasing.
Answer:
Answers may vary. Example: [2, 4]

Eureka Math Algebra 1 Module 3 Lesson 12 Exit Ticket Answer Key

Question 1.
Perform the instructions in the following programming code as if you were a computer and your paper were the computer screen:
Declare x integer
For all x from 2 to 7
If x + 2 = 7 then
Print True
else
Print False
End if
Next x
Answer:
False
False
False
True
False
False

Question 2.
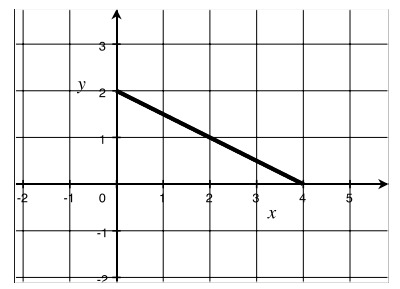
Let f(x) = – \(\frac{1}{2}\) x + 2 for x in the domain 0 ≤ x ≤ 4.
a. Write out in words the meaning of the set notation:
{(x, y) | 0 ≤ x ≤ 4 and y = f(x)}.
Answer:
The set of all points (x, y) in the Cartesian plane such that x is between 0 and 4 inclusively and y = – \(\frac{1}{2}\) x + 2 is true.

b. Sketch the graph of y = f(x).

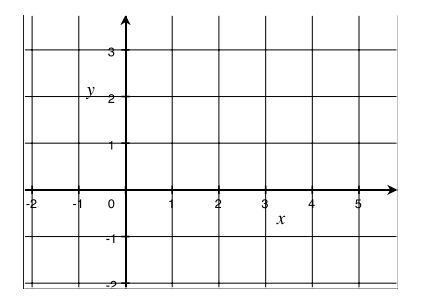
Answer: