Engage NY Eureka Math Algebra 1 Module 3 Lesson 11 Answer Key
Eureka Math Algebra 1 Module 3 Lesson 11 Exercise Answer Key
Exercise 1.
Perform the instructions in the following programming code as if you were a computer and your paper were the computer screen.
Declare x integer
For all x from 2 to 8
Print 2x + 3
Next x
Answer:
7
9
11
13
15
17
19
Exercise 2.
We can also build a set by appending ordered pairs. Perform the instructions in the following programming code as if you were a computer and your paper were the computer screen (the first few are done for you).
Declare x integer
Initialize G as {}
For all x from 2 to 8
Append (x, 2x + 3) to G
Next x
Print G
Output:
{(2, 7), (3, 9), __________________________________________}
Answer:
{(2, 7), (3, 9), (4, 11), (5, 13), (6, 15), (7, 17), (8, 19)}
Exercise 3.
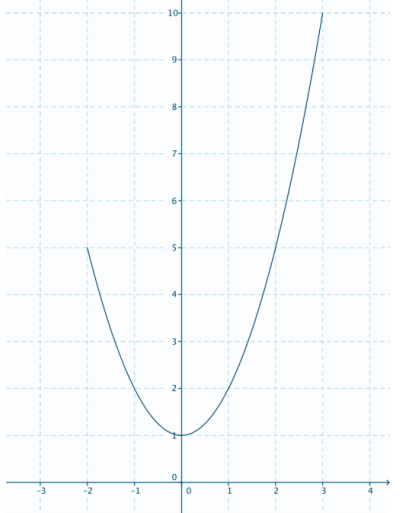
Plot the function f on the Cartesian plane using the following for-next thought code.
Declare x real
Let f(x) = x2 + 1
Initialize G as {}
For all x such that -2 ≤ x ≤ 3
Append (x, f(x) ) to G
Next x
Plot G
Answer:
b. For each step of the for-next loop, what is the input value?
Answer:
The number x
c. For each step of the for-next loop, what is the output value?
Answer:
f(x) or the value of x2 + 1
d. What is the domain of the function f?
Answer:
The interval -2 ≤ x ≤ 3
e. What is the range of the function f?
Answer:
The interval 1 ≤ f(x) ≤ 10 for all x in the domain
Eureka Math Algebra 1 Module 3 Lesson 11 Problem Set Answer Key
Question 1.
Perform the instructions for each of the following programming codes as if you were a computer and your paper were the computer screen.
Declare x integer
For all x from 0 to 4
Print 2x
Next x
Answer:
0, 2, 4, 6, 8
(Note that if replicating a computer the numbers would be printed vertically, as shown below.)
0
2
4
6
8
b.
Declare x integer
For all x from 0 to 10
Print 2x + 1
Next x
Answer:
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21
c.
Declare x integer
For all x from 2 to 8
Print x2
Next x
Answer:
4, 9, 16, 25, 36, 49, 64
d.
Declare x integer
For all x from 0 to 4
Print 10∙3x
Next x
Answer:
10, 30, 90, 270, 810
Question 2.
Perform the instructions for each of the following programming codes as if you were a computer and your paper were the computer screen.
a.
Declare x integer
Let f(x) = (x + 1)(x – 1) – x2
Initialize G as {}
For all x from -3 to 3
Append (x, f(x)) to G
Next x
Plot G
Answer:
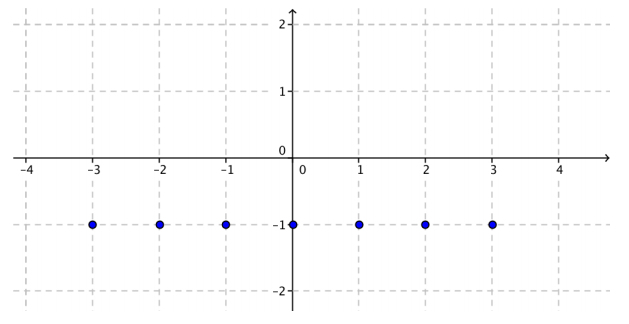
b.
Declare x integer
Let f(x) = 3-x
Initialize G as {}
For all x from -3 to 3
Append (x, f(x)) to G
Next x
Plot G
Answer:
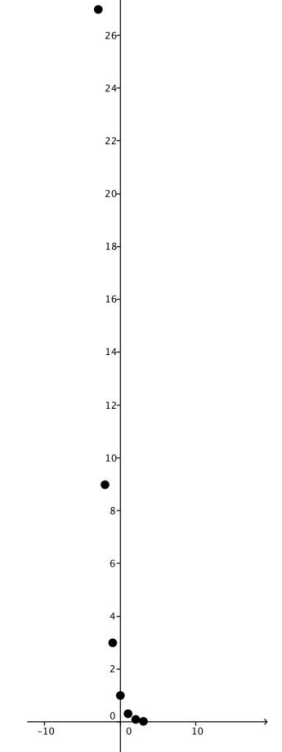
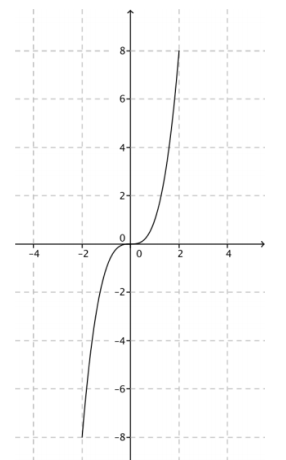
c.
Declare x real
Let f(x) = x3
Initialize G as {}
For all x such that -2 ≤ x ≤ 2
Append (x, f(x)) to G
Next x
Plot G
Answer:
Question 3.
Answer the following questions about the thought code:
Declare x real
Let f(x) = (x – 2)(x – 4)
Initialize G as {}
For all x such that 0 ≤ x ≤ 5
Append (x, f(x)) to G
Next x
Plot G
a. What is the domain of the function f?
Answer:
0 ≤ x ≤ 5
b. Plot the graph of f according to the instructions in the thought code.
Answer:
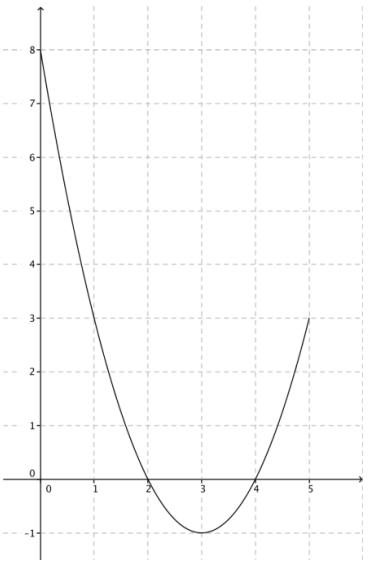
c. Look at your graph of f. What is the range of f?
Answer:
-1 ≤ f(x) ≤ 8 for all x in the domain.
d. Write three or four sentences describing in words how the thought code works.
Answer:
First, the domain of the variable x is stated as the real numbers, the formula for f is given, and the set G is initialized with nothing in it. Then the for-next loop goes through each number between 0 and 5 inclusive and appends the point (x, f(x)) to the set G. After every point is appended to G, the graph of f is plotted on the Cartesian plane.
Question 4.
Sketch the graph of the functions defined by the following formulas, and write the graph of f as a set using set-builder notation. (Hint: Assume the domain is all real numbers unless specified in the problem.)
a. f(x) = x + 2
Answer:
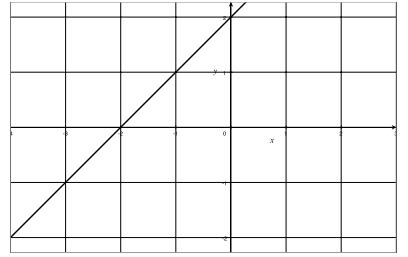
Graph of f = {(x, x + 2) | x real}
b. f(x) = 3x + 2
Answer:
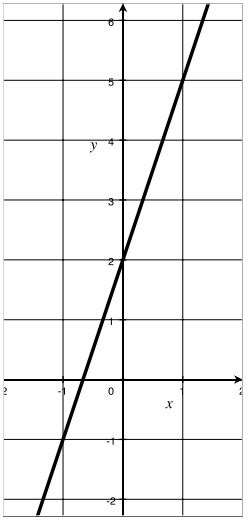
Graph of f = {(x, 3x + 2) | x real}
c. f(x) = 3x – 2
Answer:
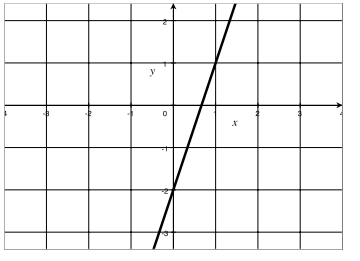
Graph of f = {(x, 3x – 2) | x real}
d. f(x) = -3x-2
Answer:
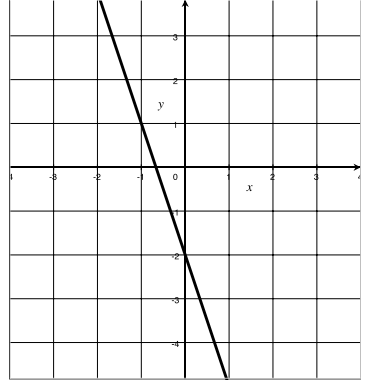
Graph of f = {(x, -3x – 2) | x real}
e. f(x) = -3x + 2
Answer:
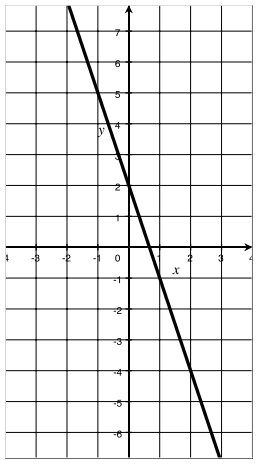
Graph of f = {(x, -3x + 2) | x real}
f. f(x) = –\(\frac{1}{3}\) x + 2, -3 ≤ x ≤ 3
Answer:
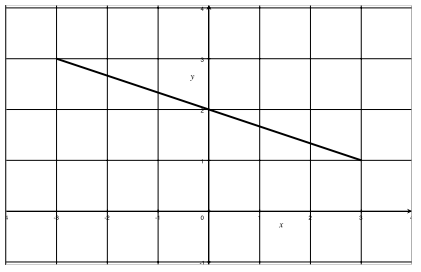
Graph of f = {(x, –\(\frac{1}{3}\) x + 2) | x real, -3 ≤ x ≤ 3} or Graph of f = {(x, –\(\frac{1}{3}\) x + 2) |-3 ≤ x ≤ 3}
g. f(x) = (x + 1)2 – x2, -2 ≤ x ≤ 5
Answer:
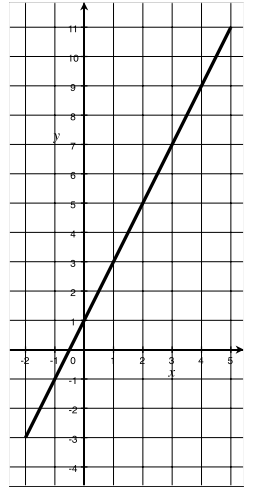
Graph of f = {(x, (x + 1)2 – x2 ) | x real, -2 ≤ x ≤ 5}
OR
Graph of f = {(x, (x + 1)2 – x2 ) |-2 ≤ x ≤ 5}
h. f(x) = (x + 1)2 – (x – 1)2, -2 ≤ x ≤ 4
Answer:
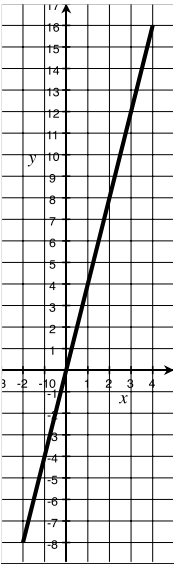
Graph of f = {(x, (x + 1)2-(x-1)2 ) | x real, -2 ≤ x ≤ 4}
OR
Graph of f = {(x, (x + 1)2-(x-1)2 ) |-2 ≤ x ≤ 4}
Question 5.
The figure shows the graph of f(x) = -5x + c.
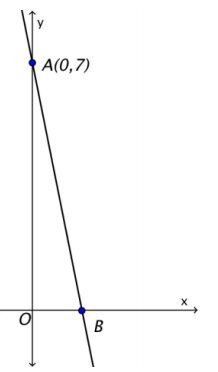
a. Find the value of c.
Answer:
c = 7
b. If the graph of f intersects the x-axis at B, find the coordinates of B.
Answer:
B(\(\frac{7}{5}\), 0)
Question 6.
The figure shows the graph of f(x) = \(\frac{1}{2}\) x + c.
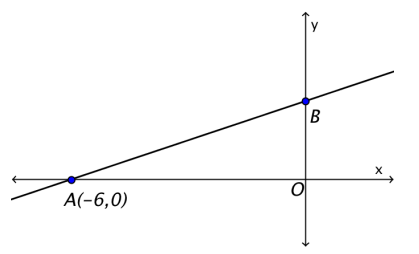
a. Find the value of c.
Answer:
c = 3
b. If the graph of f intersects the y-axis at B, find the coordinates of B.
Answer:
B(0, 3)
c. Find the area of triangle AOB.
Answer:
9 square units
Eureka Math Algebra 1 Module 3 Lesson 11 Exit Ticket Answer Key
Question 1.
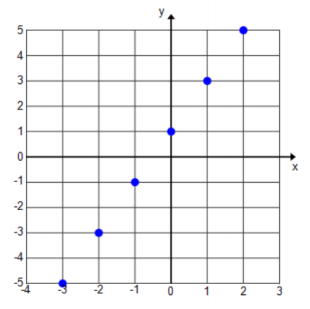
Perform the instructions for the following programming code as if you were a computer and your paper were the computer screen.
Declare x integer
Let f(x) = 2x + 1
Initialize G as {}
For all x from -3 to 2
Append (x, f(x)) to G
Next x
Plot G
Answer:
Question 2.
Write three or four sentences describing in words how the thought code works.
Answer:
The first three lines declare the domain of the variable x to be the integers, specifies the formula for f, and sets G to be the empty set with no points in it. Then the for-next loop goes through each integer between -3 and 2 inclusive and appends the point (x, f(x)) to the set G. After every point is appended to G, the graph of f is plotted on the Cartesian plane.