Engage NY Eureka Math Algebra 1 Module 3 Lesson 10 Answer Key
Eureka Math Algebra 1 Module 3 Lesson 10 Exercise Answer Key
Opening Exercise
Study the 4 representations of a function below. How are these representations alike? How are they different?
TABLE:

FUNCTION:
Let f:{0, 1, 2, 3, 4, 5} → {1, 2, 4, 8, 16, 32} such that x → 2x.
SEQUENCE:
Let a(n + 1) = 2an, a0 = 1 for 0 ≤ n ≤ 4 where n is an integer.
DIAGRAM:
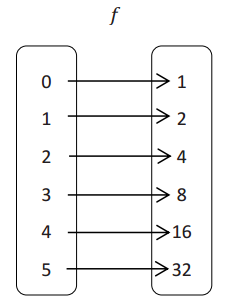
Answer:
These representations are alike because they all match the same pairs of numbers (0, 1), (1, 2), (2, 4), (3, 8), (4, 16), and (5, 32). They are different because they describe the domain, range, and correspondence differently. The table and the function look similar; the input and output are related to domain and range of a function. Evaluating the expression for the given x values returns the output values in the table, and the sequence also generates the output values for the first 6 terms starting at n = 0.
Exercise 1.
Let X = {0, 1, 2, 3, 4, 5}. Complete the following table using the definition of f.
f:X → Y
Assign each x in X to the expression 2x.

Answer:

What are f(0), f(1), f(2), f(3), f(4), and f(5)?
Answer:
f(0) = 1, f(1) = 2, f(2) = 4, f(3) = 8, f(4) = 16, and f(5) = 32
What is the range of f?
Answer:
{1, 2, 4, 8, 16, 32}
Exercise 2.
The squaring function is defined as follows:
Let f:X → Y be the function such that x → x2, where X is the set of all real numbers.
What are f(0), f(3), f( – 2), f(\(\sqrt{3}\)), f( – 2.5), f(\(\frac{2}{3}\)), f(a), and f(3 + a)?
Answer:
f(0) = 0, f(3) = 9, f( – 2) = 4, f(\(\sqrt{3}\)) = 3, f( – 2.5) = 6.25, f(\(\frac{2}{3}\)) = \(\frac{4}{9}\). To understand f(a), remind students
that x is a placeholder or a blank: (___) → (___)2, so f(a) = a2, and f(3 + a) = (3 + a)2, or f(3 + a) = 9 + 6a + a2.
What is the range of f?
Answer:
All real numbers greater than or equal to 0
What subset of the real numbers could be used as the domain of the squaring function to create a range with the same output values as the sequence of square numbers {1, 4, 9, 16, 25, …} from Lesson 9?
Answer:
Let X be the set of nonzero integers. Both the set of nonzero integers and the set of positive integers can both be domains for the squaring function. Are there any others? For example, {1, – 2, 3, – 4, 5, …}. Have a discussion with the class about why they might want to restrict the domain to just the positive integers. For example, if we wish to think about it as a sequence, we might want to restrict the domain in such a way.
Exercise 3.
Recall that an equation can either be true or false. Using the function defined by f:{0, 1, 2, 3, 4, 5} → {1, 2, 4, 8, 16, 32} such that x → 2x, determine whether the equation f(x) = 2x is true or false for each x in the domain of f.
Answer:
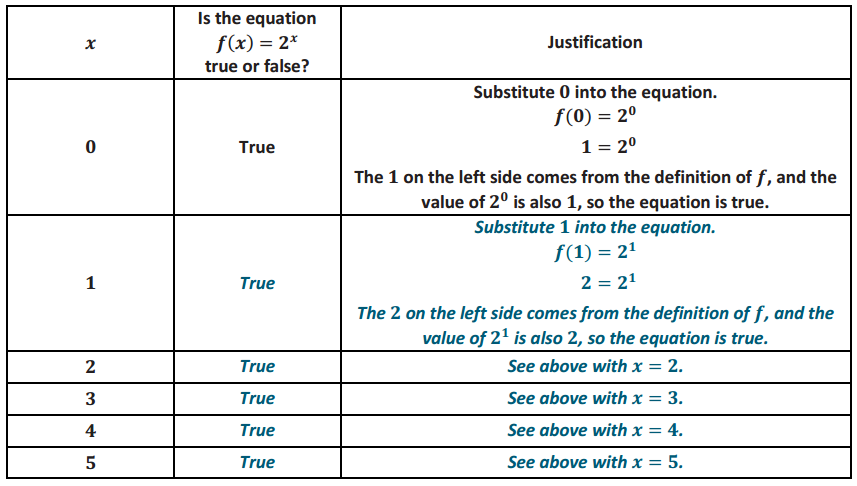
If the domain of f were extended to all real numbers, would the equation still be true for each x in the domain of f? Explain your thinking.
Answer:
Yes. Since fmaps each x → 2x, and we agreed to substitute and evaluate the expression to determine the range value for each x in the domain, the equation will always be true for every real number x.
Exercise 4.
Write three different polynomial functions such that f(3) = 2.
Answer:
f(x) = x2 – 7
f(x) = x2 – x – 4
f(x) = – 3x + 11
Exercise 5.
The domain and range of this function are not specified. Evaluate the function for several values of x. What subset of the real numbers would represent the domain of this function? What subset of the real numbers would represent its range?
Let f(x) = \(\sqrt{x – 2}\)
Answer:
f(2) = 0, f(5) = \(\sqrt{3}\), f(1) = \(\sqrt{ – 1}\). The square root of a negative number is not a real number. Therefore, the domain of this function must be real numbers greater than or equal to 2. The range is real numbers greater than or equal to 0 since the principal square root of a number is always positive. Using set notation, the domain would be D:x∈[2, ∞) and the range would be R:f(x)∈[0, ∞).
Eureka Math Algebra 1 Module 3 Lesson 10 Problem Set Answer Key
Question 1.
Let f(x) = 6x – 3, and let g(x) = 0.5(4)x. Find the value of each function for the given input.
a. f(0)
Answer:
– 3
b. f( – 10)
Answer:
– 63
c. f(2)
Answer:
9
d. f(0.01)
Answer:
– 2.94
e. f(11.25)
Answer:
64.5
f. f( – \(\sqrt{2}\))
Answer:
approx. – 11.49
g. f(\(\frac{5}{3}\))
Answer:
7
h. f(1) + f(2)
Answer:
12
i. f(6) – f(2)
Answer:
24
j. g(0)
Answer:
0.5
k. g( – 1)
Answer:
\(\frac{1}{8}\)
l. g(2)
Answer:
8
m. g( – 3)
Answer:
\(\frac{1}{128}\)
n. g(4)
Answer:
128
o. g(\(\sqrt{2}\))
Answer:
approx. 3.55
p. g(\(\frac{1}{2}\))
Answer:
1
q. g(2) + g(1)
Answer:
10
r. g(6) – g(2)
Answer:
2, 040
Question 2.
Since a variable is a placeholder, we can substitute in letters that stand for numbers for x. Let f(x) = 6x – 3, and let g(x) = 0.5(4)^x, and suppose a, b, c, and h are real numbers. Find the value of each function for the given input.
a. f(a)
Answer:
6a – 3
b. f(2a)
Answer:
12a – 3
c. f(b + c)
Answer:
6b + 6c – 3
d. f(2 + h)
Answer:
9 + 6h
e. f(a + h)
Answer:
6a + 6h – 3
f. f(a + 1) – f(a)
Answer:
6
g. f(a + h) – f(a)
Answer:
6h
h. g(b)
Answer:
0.5(4)b
i. g(b + 3)
Answer:
32(4)b
j. g(3b)
Answer:
0.5(64)b
k. g(b – 3)
Answer:
\(\frac{1}{128}\) (4)b
l. g(b + c)
Answer:
0.5(4)b + c or 0.5(4)b (4)c
m. g(b + 1) – g(b)
Answer:
\(\frac{3}{2}\) (4)b
Question 3.
What is the range of each function given below?
a. Let f(x) = 9x – 1.
Answer:
Range: All real numbers
b. Let g(x) = 32x.
Answer:
Range: All positive real numbers
c. Let f(x) = xb – 4.
Answer:
Range: f(x) ∈ [ – 4, ∞)
d. Let h(x) = \(\sqrt{x}\) + 2.
Answer:
Range: h(x)∈[2, ∞)
e. Let a(x) = x + 2 such that x is a positive integer.
Answer:
Range: a(x) is a positive integer greater than 2.
f. Let g(x) = 5x for 0 ≤ x ≤ 4.
Answer:
Range: 1 ≤ g(x) ≤ 625
Question 4.
Provide a suitable domain and range to complete the definition of each function.
a. Let f(x) = 2x + 3.
Answer:
Domain: All real numbers; Range: All real numbers
b. Let f(x) = 2x.
Answer:
Domain: All real numbers; Range: All positive real numbers
c. Let C(x) = 9x + 130, where C(x) is the number of calories in a sandwich containing x grams of fat.
Answer:
Domain: All nonnegative real numbers; Range: all real numbers greater than or equal to 130
d. Let B(x) = 100(2)x, where B(x) is the number of bacteria at time x hours over the course of one day.
Answer:
Domain: x∈[0, 24]; Range: B(x) = [100, 100 ∙ 224]
Question 5.
Let f:X → Y, where X and Y are the set of all real numbers, and x and h are real numbers.
a. Find a function f such that the equation f(x + h) = f(x) + f(h) is not true for all values of x and h. Justify your reasoning.
Answer:
Let f(x) = x2. Then, f(h) = h2, and f(x + h) = (x + h)2. The equation (x + h)2 = x2 + h2 is not true because the expression (x + h)2 is equivalent to x2 + 2xh + h2.
b. Find a function f such that equation f(x + h) = f(x) + f(h) is true for all values of x and h. Justify your reasoning.
Answer:
Let f(x) = 2x. Then f(x + h) = 2(x + h), and f(h) = 2h.
By the distributive property, 2(x + h) = 2x + 2h, and that is equal to f(x) + f(h).
c. Let f(x) = 2x. Find a value for x and a value for h that makes f(x + h) = f(x) + f(h) a true number sentence.
Answer:
If x = 1 and h = 1, then the equation f(x + h) = f(x) + f(h) can be transformed into 21 + 1 = 21 + 21, which is a true number sentence because both expressions are equal to 4.
Question 6.
Given the function f whose domain is the set of real numbers, let f(x) = 1 if x is a rational number, and let
f(x) = 0 if x is an irrational number.
a. Explain why f is a function.
Answer:
Each element of the domain (the real numbers) is assigned to one element in the range (the number 0 OR the number 1).
b. What is the range of f?
Answer:
Range: {0, 1}
c. Evaluate f for each domain value shown below.

Answer:

d. List three possible solutions to the equation f(x) = 0.
Answer:
Answers may vary. \(\sqrt{5}\), \(\sqrt{8}\), – \(\sqrt{3}\)
Eureka Math Algebra 1 Module 3 Lesson 10 Exit Ticket Answer Key
Question 1.
Let f(x) = 4(3)x. Complete the table shown below.

Answer:

Question 2.
Jenna knits scarves and then sells them on Etsy, an online marketplace. Let C(x) = 4x + 20 represent the cost C in dollars to produce 1 to 6 scarves.
a. Create a table to show the relationship between the number of scarves x and the cost C.
Answer:

b. What are the domain and range of C?
Answer:
{1, 2, 3, 4, 5, 6} and {24, 28, 32, 36, 40, 44}
c. What is the meaning of C(3)?
Answer:
The cost to produce 3 scarves
d. What is the meaning of the solution to the equation C(x) = 40?
Answer:
The number of scarves Jenna can knit for a cost of $40