Engage NY Eureka Math Algebra 1 Module 1 Lesson 4 Answer Key
Eureka Math Algebra 1 Module 1 Lesson 4 Example Answer Key
Example
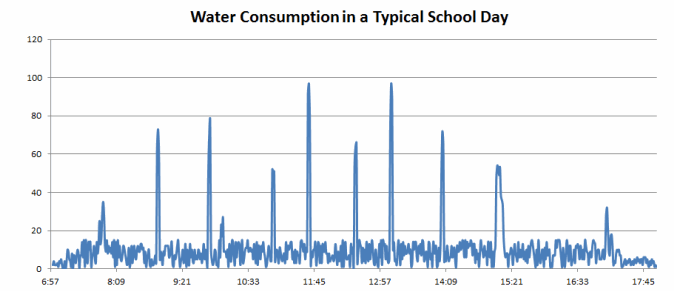
Direct students to the following graph that appears in their student materials, and ask questions about the kind of data it represents.
→ The title of the graph is “Water Consumption in a Typical School Day.” For what purposes is water used at a school?
→ Primarily through bathroom use.
→ What do you think the numbers along the horizontal axis represent?
→ Time of day.
→ What might the numbers along the vertical axis represent? Do we have any indication of the units being used?
→ Answers will vary. We have no indication of the units being used. We would assume that these numbers are related, in some way, to a volume of water.
→ What could be the reason for the spikes in the graph?
→ Student bathroom use between class periods.
→ What might be the reason for the smaller spikes between the large ones?
→ Some student use during class time.
Example
Now, offer the following further information about the typical school day for the school from which this data was recorded.
→ Regular school day hours: 8:00 a.m.–3:04 p.m.
→ After school activities: 3:15 p.m.–5:15 p.m.
→ Around 10:00 a.m. there is a 13 min. advisory or homeroom period.
Ask students:
→ Can you see features of this information appearing in the graph?
Be sure students notice the large peaks at the times just before 8:00 a.m., near 10:00 a.m., just after 3:00 p.m., and near 5:15 p.m., which can be explained by bathroom use just before and just after activities.
Ask students:
→ Is it possible to deduce the time of lunch at this school?
Students might conjecture that lunch comes in two or three shifts so as to explain the multiple large peaks in the middle of the day.
Now, return to the question of the numbers on the vertical axis:
→ Around 10:00 a.m. the graph indicates a peak of 80 units. What is the number 80 representing?
Students will likely answer “gallons of water used” or “volume of water used.” But what do we mean by used? Lead to the idea that the amount used is measured by the volume of water that drains through the pipes and leaves the school.
Then ask the question:
→ How does one actually measure the amount of water flowing out through the pipes precisely at 10:00 a.m.? What does 80 units of water leaving the school right at 10:00 a.m. mean?
→ The issue to be discussed next is that 80 units of water must take some period of time to flow out through the pipes.
Ask students to think about the bell for the end of class. At this time, they all rise and begin to walk out of the classroom, flowing through the door of the classroom. If there are 25 students in the class, would I say that a volume of 25 students is flowing through the door right at an instant? No, we have instead a flow of 25 students over a short period of time.
Ask students to consider again what the number 80 at the 10:00 a.m. mark might mean.
Now add the following information:
→ The researchers who collected this data watched the school’s water meter during a 12 hr. period. The meter shows the total amount of water (in gallons) that has left the school since the time the meter was last set to zero. Since the researchers did not know when this resetting last occurred, they decided, at each minute mark during the day, to measure how much the meter reading increased over the next minute of time. Thus, the value 80 at the 10:00 a.m. mark on the graph means that 80 gal. of water flowed through the meter and left the school during the period from 10:00 a.m. to 10:01 a.m.
Ask students:
→ What are the units for the numbers on the vertical axis?
→ The units for the numbers on the vertical axis are gallons per minute.
→ Ignoring the large spikes in the graph, what seems to be the typical range of values for water use during the school day?
Help students notice that the value of the graph between the large spikes seems to oscillate between the flow of 0 gal. of water per minute and about 15 gal. of water per minute.
Now have students complete Exercises 1 and 2 independently and then work in pairs or in small groups to discuss approaches and compare answers. Ask students to volunteer their answers to a general class discussion. Discuss any assumptions that were made to arrive at answers.
Eureka Math Algebra 1 Module 1 Lesson 4 Exercise Answer Key
Exercises 1–2
Exercise 1.
The bulk of water usage is due to the flushing of toilets. Each flush uses 2.5 gal. of water. Samson estimates that 2% of the school population uses the bathroom between 10:00 a.m. and 10:01 a.m. right before homeroom. What is a good estimate of the population of the school?
Answer:
We know that 80 gallons of water are used during that minute. This corresponds to \(\frac{80}{2.5}\)=32 flushes. Assuming that each student flushes just once, we can say that 32 students used the bathroom during this time. This represents 2% of the school population, which is one fiftieth of the school population. Thus, there are about 1,600 people at the school.
Exercise 2.
Samson then wonders this: If everyone at the school flushed a toilet at the same time, how much water would go down the drain (if the water pressure of the system allowed)? Are we able to find an answer for Samson?
Answer:
Answers will vary based on assumptions made. If there were enough toilets that everyone could flush a toilet at the same time, and using the estimated school population of 1,600 (there would have to be 1,600 toilets), then 1600×2.5 gal.=4000 gal. of water.
Exercise 3:
Estimation Exercise
a. Make a guess as to how many toilets are at the school.
Answer:
80
b. Make a guess as to how many students are in the school, and what percentage of students might be using the bathroom at break times between classes, just before the start of school, and just after the end of school. Are there enough toilets for the count of students wishing to use them?
Answer:
Of 1,600 students, at any given break time, 20% are using the restroom. That means that during a break time 320 students wish to use the toilet. Since there are only approximately 80 toilets, there are not enough toilets if all of the students go at the same time (say at the beginning of the break).
c. Using the previous two considerations, estimate the number of students using the bathroom during the peak minute of each break.
320 students are using the bathroom during a break, but maybe only \(\frac{1}{4}\) of them at any one minute, so 80 at any one minute.
d. Assuming each flush uses 2.5 gal. of water, estimate the amount of water being used during the peak minute of each break.
Answer:
80 flushes×2.5 \(\frac{\text { gal }}{\text { flush }}\)=200 gal.
e. What time of day do these breaks occur? (If the school schedule varies, consider today’s schedule.)
Answer:
Answers will vary by school; an example: 8:00, 9:45, 11:30, 12:00, 1:45, 3:30
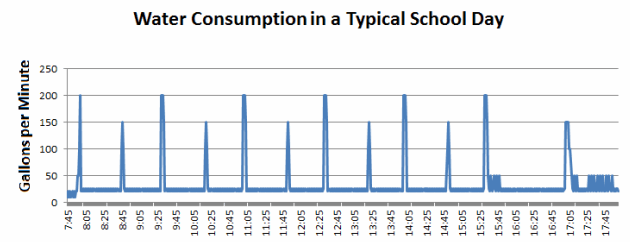
f. Draw a graph that could represent the water consumption in a typical school day of your school.
Answer:
Eureka Math Algebra 1 Module 1 Lesson 4 Exit Ticket Answer Key
Suppose the researchers collecting data for water consumption during a typical school day collected data through the night too.
Question 1.
For the period between the time the last person leaves the building for the evening and the time of the arrival of the first person the next morning, how should the graph of water consumption appear?
Answer:
Since no toilets are being used, the graph should be a horizontal line of constant value zero.
Question 2.
Suppose the researchers see instead, from the time 1:21 a.m. onward, the graph shows a horizontal line of constant value, 4. What might have happened during the night?
Answer:
Perhaps one toilet started to leak at 1:21 a.m., draining water at a rate of 4 gallons per minute.
Eureka Math Algebra 1 Module 1 Lesson 4 Problem Set Answer Key
Question 1.
The following graph shows the temperature (in degrees Fahrenheit) of La Honda, CA in the months of August and September of 2012. Answer the questions following the graph.
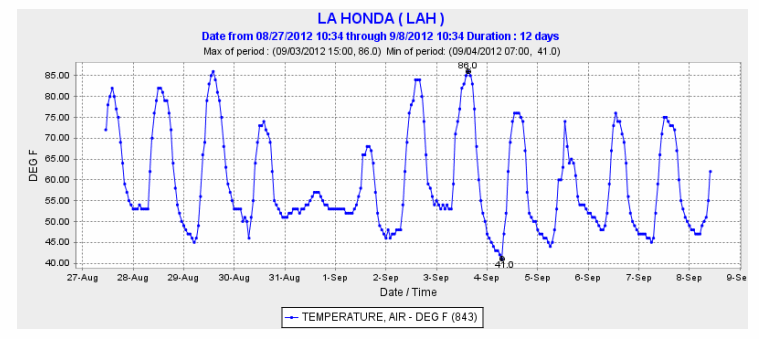
a. The graph seems to alternate between peaks and valleys. Explain why.
Answer:
The temperature increases during the day and drops during the night, and the difference between the high and low temperatures can be very large.
b. When do you think it should be the warmest during each day? Circle the peak of each day to determine if the graph matches your guess.
Answer:
The warmest time should be before sunset, a few hours after noon, since heating occurs throughout the day while the sun is up.
c. When do you think it should be the coldest during each day? Draw a dot at the lowest point of each day to determine if the graph matches your guess.
Answer:
Similarly, the coldest temperature should be before sunrise, since cooling occurs throughout the night.
d. Does the graph do anything unexpected such as not following a pattern? What do you notice? Can you explain why it is happening?
Answer:
The graph seems to follow the expected pattern with natural variations, except for the unusually low daytime temperatures on August 31.
Question 2.
The following graph shows the amount of precipitation (rain, snow, or hail) that accumulated over a period of time in La Honda, CA.
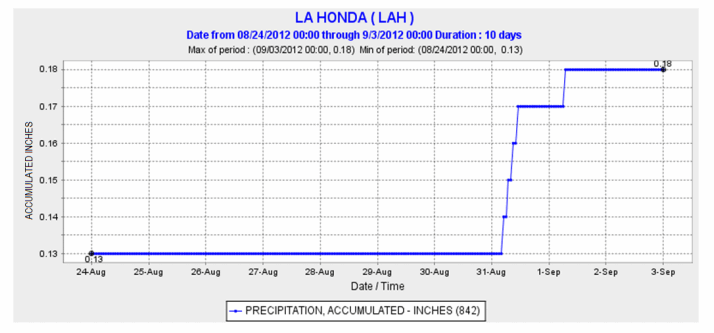
a. Tell the complete story of this graph.
Answer:
On August 24, the measurement started with an initial cumulative data of 0.13 in. It stands for the precipitation accumulated before the current measurement. Nothing else happened until August 31, when there was 0.04 in. of precipitation. On September 1, there was 0.01 in. more of precipitation.
b. The term accumulate, in the context of the graph, means to add up the amounts of precipitation over time. The graph starts on August 24. Why didn’t the graph start at 0 in. instead of starting at 0.13 in.?
Answer:
On August 24, the measurement started with an initial cumulative data of 0.13 in. It stands for the precipitation accumulated before the current measurement.
Question 3.
The following graph shows the solar radiation over a period of time in La Honda, CA. Solar radiation is the amount of the sun’s rays that reach the earth’s surface.
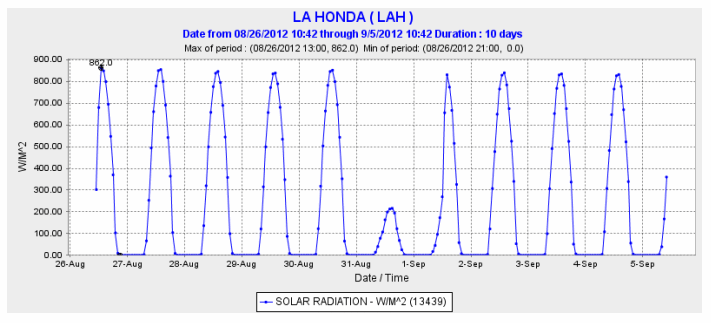
a. What happens in La Honda when the graph is flat?
Answer:
This represents time periods during which the solar radiation per unit area is constant. For example, during nighttime, there is no sunlight, and hence there are flat regions on the curve.
b. What do you think is happening when the peaks are very low?
Answer:
It could be an overcast day. Other less common events, such as a solar eclipse, would also cause this.
c. Looking at all three graphs, what do you conclude happened on August 31, 2012 in La Honda, CA?
Answer:
The lower temperature, increase in accumulated precipitation, and the low solar radiation makes me think that August 31, 2012 was overcast and rainy for most of the day.
Question 4.
The following graph shows the velocity (in centimeters per second) and turbidity of the Logan River in Queensland, Australia during a flood. Turbidity refers to the clarity of the water (higher turbidity means murkier water) and is related to the total amount of suspended solids, such as clay, silt, sand, and phytoplankton, present in the water.
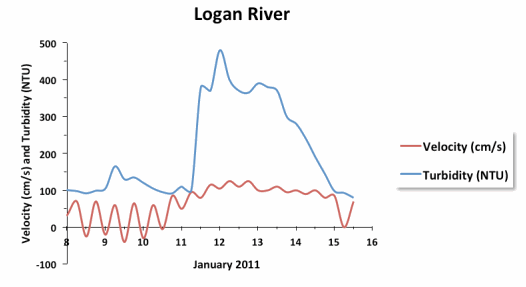
a. For recreation, Jill visited the river during the month of January and saw clean and beautiful water. On which day do you think she visited?
Answer:
The fifteenth appears to be the best choice because of the low turbidity. The eighth and tenth are also good choices.
b. What do the negative velocities (below the grey line) that appear periodically at the beginning represent?
Answer:
This shows normal tidal flow, which is disturbed during the flood.
c. The behavior of the river seems to follow a normal pattern at the beginning and at the very end of the time period shown. Approximately when does the flood start? Describe its effects on velocity and turbidity.
Answer:
The flood starts on the eleventh. It increases the velocity so that it is always positive, disturbing the tide, and it increases the turbidity of the water.