Engage NY Eureka Math Algebra 1 Module 1 Lesson 25 Answer Key
Eureka Math Algebra 1 Module 1 Lesson 25 Exercise Answer Key
Exercise 1.
a. Solve the following problem first using a tape diagram and then using an equation: In a school choir, \(\frac{1}{2}\) of the members were girls. At the end of the year, 3 boys left the choir, and the ratio of boys to girls became 3:4. How many boys remained in the choir?
Answer:
Using a tape diagram: Using an equation:
Initially:
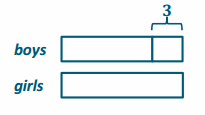
Using an equation:
# of boys initially: b
# of girls initially: b
# of boys at the end of the year: b-3
Ratio of boys to girls at the end of the year: b-3:b=3:4
At end of year:
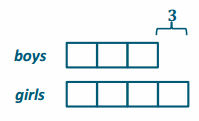
1 unit =3 boys
3 units =9 boys
There are 9 boys in the choir.
Therefore,
\(\frac{b-3}{b}\)=\(\frac{3}{4}\)
b∙(\(\frac{b-3}{b}\))=(\(\frac{3}{4}\))∙b
b-3=\(\frac{3}{4}\) b
b-3-\(\frac{3}{4}\) b=\(\frac{3}{4}\) b-\(\frac{3}{4}\) b
\(\frac{1}{4}\) b-3=0
\(\frac{1}{4}\) b-3+3=0+3
4(\(\frac{1}{4}\) b)=(3)4
b=12
The number of boys remaining in the choir is 12-3, or 9.
b. Which problem solution, the one using a tape diagram or the one using an equation, was easier to set up and solve? Why?
Answer:
Answers will vary. Most should say the tape diagram since it requires significantly less work than solving the problem algebraically. Point out that this may not always be the case.
→ Modify the question so that the tape diagram solution would definitely not be the easier way to solve the problem.
Sample question: In a school choir, \(\frac{6}{11}\) of the members were girls. At the end of the year, 3 boys had left the choir, and the ratio of the number of boys to the number of girls was 3:4. How many boys remained in the choir?
Mathematical Modeling Exercise/Exercise 2
Read the following problem:
All the printing presses at a print shop were scheduled to make copies of a novel and a cookbook. They were to print the same number of copies of each book, but the novel had twice as many pages as the cookbook. All of the printing presses worked for the first day on the larger book, turning out novels. Then, on day two, the presses were split into two equally sized groups. The first group continued printing copies of the novel and finished printing all the copies by the evening of the second day. The second group worked on the cookbook but did not finish by evening. One printing press, working for two additional full days, finished printing the remaining copies of the cookbooks. If all printing presses printed pages (for both the novel and cookbook) at the same constant rate, how many printing presses are there at the print shop?
Analyze the problem with your students, rereading the problem together as you answer questions like:
→ What is this story about?
→ Printing novels and cookbooks.
→ Will more novels be printed than cookbooks or fewer?
→ Neither. The same number of each will be printed.
→ How many pages does the novel have compared to the cookbook?
→ Twice as many as the cookbook.
→ How much longer would one printing press take to print a novel versus a cookbook?
→ Twice as long.
→ Is it important to know how many pages each book has or how many of each book will need to be printed? Why?
→ No. Answers will vary.
→ How many of the printing presses are used to print the novel on the first day?
→ All of them.
→ How many of the printing presses are used to print the novel on the second day?
→ One half of them.
→ How many of the printing presses are used to print the cookbook on the second day?
→ One half of them.
→ How many printing presses are used to print the remainder of the cookbooks on the third and fourth days?
→ One.
→ How many printing presses could be used to print the remainder of the cookbooks in one day instead of two?
→ Two printing presses could have finished the cookbooks on the third day.
→ What are we trying to find in this problem?
→ The number of printing presses at the print shop.
a. Solve the problem working with rates to setup a tape diagram or an area model.
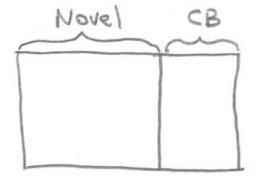
One of the keys to a (somewhat) simple solution using an area model is recognizing that the novel has twice as many pages as the cookbook, so the area that represents the novel job should be twice the size as the area used to represent the cookbook job.
Draw a rectangular region to represent the work needed to complete the novel job and another rectangular region, half the size, to represent the work needed to complete the cookbook job.
On the first day, all the printing presses were used on printing copies of the novel, and on the second day, half completed the novel while half worked on the cookbook.
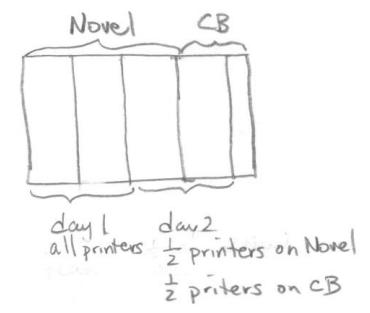
Students can test conjectures on why the novel job is split into thirds. For example, if all printing presses completed \(\frac{1}{2}\) of the novel job on day one, then \(\frac{1}{2}\) of the printing presses would only complete \(\frac{1}{4}\) of the job on day two. Therefore, only \(\frac{3}{4}\) of the novel job would be complete by the end of day two. But the story says the whole novel job is complete by the end of day two (i.e., something is wrong with that conjecture).
Once students understand that the novel job must be split into thirds, label the novel job as the “whole unit” and each third unit as the fractional unit “\(\frac{1}{3}\) of the whole.” The cookbook job is then “\(\frac{1}{2}\) of the whole.” The same \(\frac{1}{3}\) unit must have
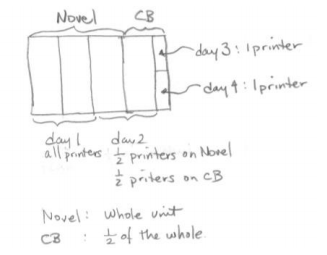
also been completed on the cookbook job on day two, leaving \(\frac{1}{2}\)–\(\frac{1}{3}\)=\(\frac{1}{6}\) of the whole unit left for days three and four.
Each of the small rectangles in the picture above represents how much of the whole job (i.e., the novel job) one printing press can do in one day. Drawing in the small rectangle units into the rest of the diagram, one sees that eight printing presses worked on the novel job on day one, which was all of the printing presses. Hence, there are eight printing presses at the print shop. Students now know there are eight printing presses at the workshop. This should help them confirm their solution paths in Exercise 2 part (b).
b. Solve the problem by setting up an equation.
Start by asking students to write down all variables for the quantities they see in the problem, giving an appropriate letter for each. While it does not matter if they work with the number of copies of cookbooks or the number of pages per cookbook, guide them to use the number of copies of cookbooks as you walk around your class. (Tell students not to worry about writing down too many letters—there is no need to write all of them.)
Be careful not to write “printing presses =x” on the board. Such a statement abuses how the = symbol should be used. Such statements do not make sense—printing presses are not numbers. It is a good idea to require students to develop the habit of always properly labeling their variables using short descriptions (e.g., number of printing presses: x). This habit can help them significantly in setting up equations and solving algebra problems.
Answer:
Number of printing presses: x. (This is what we wish to find.)
Number of copies of cookbooks printed by one printing press in one day: r.
Number of copies of novels printed by one printing press in one day: \(\frac{1}{2}\) r. (Only half the number of novels can be produced each day.)
Number of copies in the cookbook job: c.
Number of copies in the novel job: c.
Next, ask students to write down important expressions using the variables above. There are many valid possible expressions they can write down that can be used to solve the problem. Here is one possible list:
Answer:
Novels:
Number of copies of novels printed in one day by the entire print shop: \(\frac{1}{2}\) rx.
Number of copies of novels printed in one day by half of the entire print shop: \(\frac{1}{4}\) rx.
Total number of copies of novels printed: \(\frac{1}{2}\) rx+\(\frac{1}{4}\) rx, or \(\frac{3}{4}\) rx.
Cookbooks:
Number of copies of cookbooks printed in one day by half of the entire print shop: \(\frac{1}{2}\) rx.
Number of copies of cookbooks printed in two days by one printing press: 2r.
Total number of copies of cookbooks printed: \(\frac{1}{2}\) rx+2r.
Since the number of cookbooks and novels is the same, we can equate the expressions of the totals above to get:
\(\frac{3}{4}\) rx=\(\frac{1}{2}\) rx+2r.
Since r is known not to be zero, we can divide both sides of the equation by r, and solve the resulting equation for x:
Answer:
\(\frac{3}{4}\) x=\(\frac{1}{2}\) x+2
\(\frac{3}{4}\) x-\(\frac{1}{2}\) x=\(\frac{1}{2}\) x+2-\(\frac{1}{2}\) x
\(\frac{1}{4}\) x=2
4(\(\frac{1}{4}\) x)=4(2)
x=8
Check by substituting 8 back into the original equation. The left-hand side is \(\frac{3}{4}\) r(8)=6r, which is equal to the right-hand side, \(\frac{1}{2}\) r(8)+2r=4r+2r=6r.
There are 8 printing presses in the print shop.
Because there are a number of ways to set up a correct equation, students will inevitably create several solution paths. If time permits, explore the different solution paths with students. Help them see that their solutions are just as valid as the teacher’s.
Eureka Math Algebra 1 Module 1 Lesson 25 Problem Set Answer Key
Question 1.
Solve the following problems first using a tape diagram and then by setting up an equation. For each, give your opinion on which solution method was easier. Can you see the connection(s) between the two methods? What does each “unit” in the tape diagram stand for?
a. 16 years from now, Pia’s age will be twice her age 12 years ago. Find her present age.
Tape:
Answer:
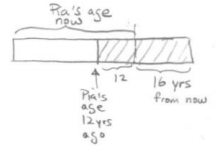
1 unit = 12 + 16 = 28
28 + 12 = 40
Pia is 40 years old.
Equation:
Answer:
Pia’s age now : P years old
p + 16 = 2(p – 12)
p + 16 = 2p – 24
p + 16 + 24 = 2p – 24 + 24
p + 40 = 2p
p + 40 – p = 2p – p
40 = p
Check: 40 + 16 = 2(40 – 12)
56 = 56 ✓
Pia is 40 years old.
b. The total age of a woman and her son is 51 years. Three years ago, the woman was eight times as old as her son. How old is her son now?
Answer:
Tape:
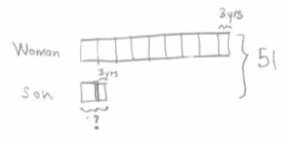
9 units + 6 = 51
9 units = 45
1 unit = 5
5 + 3 = 8
Equation:
Answer:
Son’s age : S years old
Woman’s age: 51 – S
Equation : 51 – S – 3 = 8(S – 3)
Solve:
48 – S = 8S – 24
48 – S + S = 8S – 24 + S
48 = 9S – 24 + 24
48 + 24 = 9S – 24 + 24
72 = 9S
8 = S
Check:
If son is 8 year old now, then the woman is 43 year old.
Three year ago :
woman – 40
Son – 5
The sun is 8 years old.
c. Five years from now, the sum of the ages of a woman and her daughter will be 40 years. The difference in their present age is 24 years. How old is her daughter now?
Tape:
Answer:
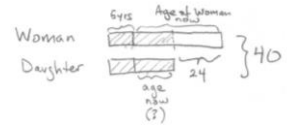
shaded part is a unit
2 units + 24 = 40
2 units = 16
1 unit = 8
8 – 5 = 3
The daughter is 3 years old.
Equation:
Answer:
Daughter’s age now = d years old
Woman’s age now = d + 24
Equation : (d + 5) + (d + 24 + 5) = 40
Solve:
2d + 34 = 40
2d + 34 – 34 = 40 – 34
2d = 6
\(\frac{1}{2}\)(2d) = \(\frac{1}{2}\)(6)
d = 3
Check: Woman’s age now = 27 years
In 5 years,
Woman is 32
daughter is 8
Sum is 40
Daughter is 3 years old
d. Find three consecutive integers such that their sum is 51.
Tape:
Answer:
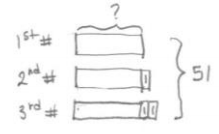
3 units + 3 = 51
3 units = 48
1 unit = 16
The consecutive numbers are 16, 17, 18.
Equation:
Answer:
1st number = x
2nd number = x + 1
31rd number = x + 2
Equation:
x + (x + 1) + (x + 2) = 51
Solve:
3x + 3 = 51
3x + 3 – 3 = 51 – 3
3x = 48
\(\frac{1}{3}\)(3x) = \(\frac{1}{3}\)(48)
x = 16
Check: 16 + 17 + 18 = 51 ✓
The three consecutive numbers are 16, 17, 18.
Question 2.
Solve the following problems by setting up an equation or inequality.
a. If two numbers represented by (2m+1) and (2m+5) have a sum of 74, find m.
Answer:
Equation: (2m + 1) + (2m + 5) = 74
Solve: 4m + 6 = 74
4m + 6 – 6 = 74 – 6
4m = 68
\(\frac{1}{4}\)(4m) = \(\frac{1}{4}\)(68)
m = 17
Check: 2∙17 + 1 + 2∙17 + 5 = 68 + 6 = 74 ✓
The number m is 17.
b. Find two consecutive even numbers such that the sum of the smaller number and twice the greater number is 100.
Answer:
1st number = x
2nd number = x + 2
Equation : x + 2(x + 2) = 100
3x + 4 = 100
3x = 96
\(\frac{1}{3}\)(3x) = \(\frac{1}{3}\)(96)
x = 32
Check: 32 + 2(34) = 32 + 68 = 100 ✓
The numbers are 32 and 34.
c. If 9 is subtracted from a number, and the result is multiplied by 19, the product is 171. Find the number.
Answer:
Number: n
Equation : 19(n – 9) = 171
Solve: \(\frac{1}{19}\)(19(n – 9)) = \(\frac{1}{19}\)(171)
n – 9 = 9
n = 18
Check: 19(8 -9) = 19∙19 = 171 ✓
The number is 18.
d. The product of two consecutive whole numbers is less than the sum of the square of the smaller number and 13.
Answer:
1st number = m
2nd number = m + 1
Equation: m(m + 1) < m2 + 13
Solve: m2 + m < m2 + 13 – m2
m < 13
Since m is a whole number : 0 ≤ m < 13
Check: 0.1 < 13
1.2 < 12 + 13 ✓
2.3 < 22 + 13 ✓
.
.
.
.
12.13 < 122 + 13 ✓
13.14 < 132 + 13 ✗
Question 3.
The length, 18 meters, is the answer to the following question.
“The length of a rectangle is three meters longer than its width. The area of the rectangle is 270 square meters. What is the length of the rectangle?”
Rework this problem: Write an equation using L as the length (in meters) of the rectangle that would lead to the solution of the problem. Check that the answer above is correct by substituting 18 for L in your equation.
Answer:
Length (in meters): L
Width (in meters): L-3
Equation: L(L-3)=270
Check: 18(18-3)=18∙15=270
Question 4.
Jim tells you he paid a total of $23,078.90 for a car, and you would like to know the price of the car before sales tax so that you can compare the price of that model of car at various dealers. Find the price of the car before sales tax if Jim bought the car in each of the following states:
a. Arizona, where the sales tax is 6.6%.
Answer:
Solving x(1+0.066)=2 307 8.90 results in x=21 650. The car costs $21,650.
b. New York, where the sales tax is 8.25%.
Solving x(1+0.0825)=2 307 8.90 results in x=21 320. The car costs $21,320.
c. A state where the sales tax is s%.
Answer:
Solving x(1+\(\frac{s}{100}\))=2 307 8.90 results in x=\(\frac{2307890}{100+s}\). For a sales tax of s%, the car costs \(\frac{2307890}{100+s}\) dollars.
Question 5.
A checking account is set up with an initial balance of $9,400, and $800 is removed from the account at the end of each month for rent. (No other user transactions occur on the account.)
a. Write an inequality whose solutions are the months, m, in which the account balance is greater than $3,000. Write the solution set to your equation by identifying all of the solutions.
Answer:
For m a nonnegative real number, m satisfies the inequality, 9400-800m>3000. For real numbers m, the solution set is 0≤m<8.
b. Make a graph of the balance in the account after m months and indicate on the plot the solutions to your inequality in part (a).
Answer:
Students can create a step-function (like below), or simply plot the points (with no lines drawn). Drawing a straight line through the points, however, does not accurately reflect the information in the problem.
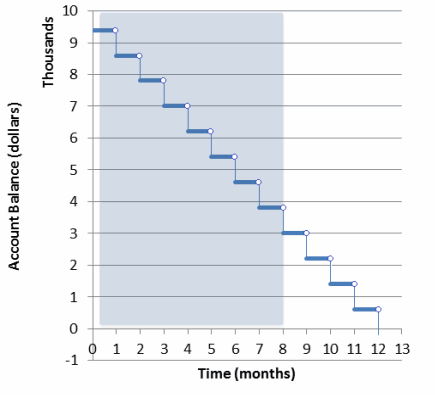
Question 6.
Axel and his brother like to play tennis. About three months ago they decided to keep track of how many games each has won. As of today, Axel has won 18 out of the 30 games against his brother.
a. How many games would Axel have to win in a row in order to have a 75% winning record?
Answer:
Solving 18+n=0.75(30+n) results in n=18. He would have to win 18 games.
b. How many games would Axel have to win in a row in order to have a 90% winning record?
Answer:
Solving 18+n=0.90(30+n) results in n=90. He would have to win 90 games.
c. Is Axel ever able to reach a 100% winning record? Explain why or why not.
Answer:
No. A 100% winning record would mean solving the equation 18+n=1(30+n), which has no solutions.
d. Suppose that after reaching a winning record of 90% in part (b), Axel had a losing streak. How many games in a row would Axel have to lose in order to drop down to a winning record of 60% again?
Answer:
Solving, 108=0.60(120+n), results in n=60. He would have to lose 60 games.
Question 7.
Omar has $84 and Calina has $12. How much money must Omar give to Calina so that Calina will have three times as much as Omar?
a. Solve the problem above by setting up an equation.
Answer:
Solution 1:
Amount Omar gives: x dollars.
Amount Omar has after giving: 84-x.
Amount Calina has after: 12+x.
Equation: 12+x=3(84-x).
Solve:
12+x=252-3x
12+x+3x=252-3x+3x
12+4x=252
12+4x-12=252-12
4x=240
\(\frac{1}{4}\)(4x)=\(\frac{1}{4}\)(240)
x=60
Check: Omar now has $24 and Calina has $72, which is three times as much as Omar.
Solution 2:
A few students might notice that if Calina has three times as much as Omar afterwards, and if we let y be the amount that Omar has after, then y+3y=96, or y=24. Now it is easy to find out how much Omar gave.
b. In your opinion, is this problem easier to solve using an equation or using a tape diagram? Why?
Answer:
Most likely, students will say it is easier to solve with an equation because it is easier to set up and solve. (They may show an attempt at drawing a tape diagram, for example.) However, students who used the second solution may respond that the tape diagram is easier.
Eureka Math Algebra 1 Module 1 Lesson 25 Exit Ticket Answer Key
Suppose we know that the print shop had 8 printing presses, and each printing press runs at a constant speed of 5,000 pages per hour for 6 hours a day.
Question 1.
Compute the total number of pages printed for the cookbook job and the total number of pages printed for the novel job following the schedule and situation described in Exercise 2(a).
Answer:
Number of pages printed by a printing press in 1 day: 30,000
Number of pages printed by 8 printing presses in 1 day: 240,000
Number of pages printed by 8 printing presses in 2 days: 480,000
Number of pages 1 printing press prints in 2 days: 60,000
Number of pages printed for both jobs: 60 000+480 000=540 000.
Ratio of number of pages of the novel to the number of pages of the cookbook: 2:1.
Therefore, 360,000 pages for the novel and 180,000 for the cookbook.
Question 2.
Describe a scenario where it would make sense for the job scheduler to schedule both jobs as described in Exercise 2 part (a).
The client for the novel job wants the print job completed by midweek, whereas the cookbook does not need to be completed until the end of the week.
BONUS
Question 3.
If the novel was 250 pages and the cookbook 125 pages, how many copies of each were printed?
Answer:
1,440 copies of each were printed.