Engage NY Eureka Math Algebra 1 Module 1 Lesson 20 Answer Key
Eureka Math Algebra 1 Module 1 Lesson 20 Exercise Answer Key
Exercises
Exercise 1.
Circle all the ordered pairs (x,y) that are solutions to the equation 4x-y=10.
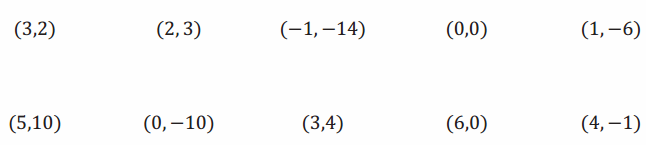
Answer:
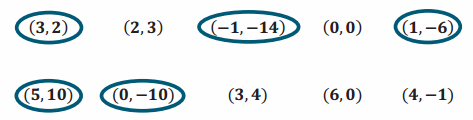
b. How did you decide whether or not an ordered pair was a solution to the equation?
Answer:
Most students will explain that they substituted and checked to see whether or not the equation was true.
Point out the two-variable equation in Exercise 1 and the possible solutions represented as ordered pairs. Working independently, students use their prior knowledge to verify which ordered pairs are solutions to an equation. Ask students to compare their solutions with a partner. Briefly share answers, and give students a chance to revise their work or add to their written responses to part (b).
Exercise 2.
Students should work in groups on Exercise 2 part (a) only. After about four minutes, have each group share their solutions and their solution strategies with the entire class. Highlight the different approaches to finding solutions. Most groups will likely start by picking a value for either x or y and then deciding what the other variable should equal to make the number sentence true. Value groups that began to organize their solutions in a meaningful way, such as by increasing x-values. Groups may even organize their solutions in a graph.
Exercise 2.
a. Discover as many additional solutions to the equation 4x-y=10 as possible. Consider the best way to organize all the solutions you have found. Be prepared to share the strategies you used to find your solutions.
Answer:
Sample answers: (-5,-30); (-2,-18); (2,-2); (4,6)
b. Now, find five more solutions where one or more variables are negative numbers or non-integer values. Be prepared to share the strategies you used to find your solutions.
Answer:
Sample answers: (-4,-26); (-3,-22); (\(\frac{1}{2}\),-8); (\(\frac{3}{2}\),-4); (\(\frac{5}{2}\),0)
c. How many ordered pairs (x,y) will be in the solution set of the equation 4x-y=10?
Answer:
Infinitely many.
d. Create a visual representation of the solution set by plotting each solution as a point (x,y) in the coordinate plane.
Answer:
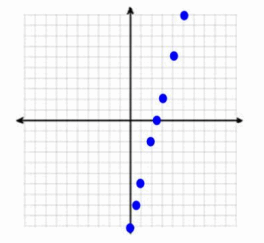
e. Why does it make sense to represent the solution to the equation 4x-y=10 as a line in the coordinate plane?
Answer:
Drawing the line is the only way to include all possible solutions. It would be impossible to plot every point that is a solution to the equation since there are infinitely many solutions.
Next, have the groups complete parts (b) through (d). Debrief the entire class by having each group share their work, or if time permits, create a class graph. Parts (c) and (e) are the most important. Students need to realize that listing all the solutions is impossible. A visual representation of a curve (in this case a line) is a way to include ALL possible solutions including those with fractional or irrational values. Prove this to students by letting x=\(\sqrt{2}\) and then solving for y=4\(\sqrt{2}\) -10. Then, use a graphing calculator or graphing software to graph the line and find the value when x=\(\sqrt{2}\) .
Exercises 3–5 (15 minutes)
These exercises ask students to create a linear equation in two variables that represents a situation. The equations in Exercises 3 and 4 are the same, but the domain of each variable is different due to the context. Require students to attend to precision in depicting answers that reflect the domain given the context. Are they using “let” statements to name each variable? Are they getting correct solutions to the equations? Notice whether or not they are using some of the strategies developed in the exercise to find their solutions. In Exercise 3, the graph should be a solid line that extends to the boundaries of the coordinate plane, but in Exercise 4, the graph should be discrete and only contain whole number values in the ordered pairs.
Exercise 3.
The sum of two numbers is 25. What are the numbers?
a. Create an equation using two variables to represent this situation. Be sure to explain the meaning of each variable.
Answer:
Let x= one number, and let y= another number.
Equation: x+y=25
Answer:
b. List at least six solutions to the equation you created in part (a).
Answer:
Answers will vary but should be pairs of numbers whose sum is 25.
c. Create a graph that represents the solution set to the equation.
Answer:
See graph to the right.
Question 4.
Gia had 25 songs in a playlist composed of songs from her two favorite artists, Beyonce and Jennifer Lopez. How many songs did she have by each one in the playlist?
a. Create an equation using two variables to represent this situation. Be sure to explain the meaning of each variable.
Answer:
Let x= the number of Beyonce songs, and let y= the number of Jennifer Lopez songs. Equation: x+y=25
b. List at least three solutions to the equation you created in part (a).
Answer:
Answers will vary but should be limited to pairs of whole numbers whose sum is 25.
c. Create a graph that represents the solution set to the equation.
Answer:
See graph to the right.
Question 5.
Compare your solutions to Exercises 3 and 4. How are they alike? How are they different?
Answer:
The solution set to Exercise 3 is an infinite number of ordered pairs, and the graph is a solid line. The solution set to Exercise 4 is a finite set of ordered pairs that also happens to be in the solution set to Exercise 3. The graph is a discrete set of points that lie on the line y=-x+25.
When debriefing these exercises with the whole class, be sure to reinforce that the domain depends on the situation. Review expectations for making a complete graph (scaling, labeling, etc.). Emphasize the difference between a discrete and continuous graph.
Eureka Math Algebra 1 Module 1 Lesson 20 Problem Set Answer Key
Question 1.
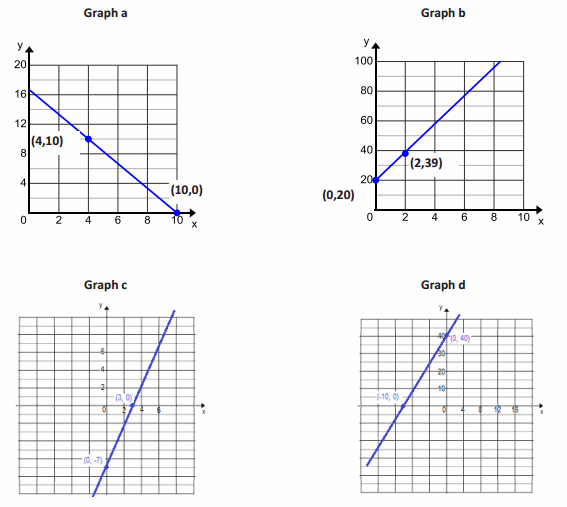
Match each equation with its graph. Explain your reasoning.
Answer:
Justifications will vary. Sample response: I identified points on each graph and substituted them into the equations. Some graphs had the same points, like (0,-6), so I needed to check the solutions with at least one other point.
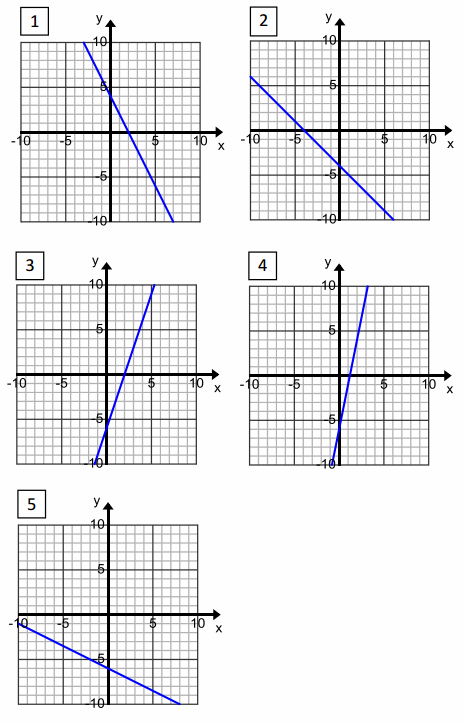
a. y=5x-6
Answer:
Graph 4
b. x+2y=-12
Answer:
Graph 5
c. 2x+y=4
Answer:
Graph 1
d. y=3x-6
Answer:
Graph 3
e. x=-y-4
Answer:
Graph 2
Question 2.
Graph the solution set in the coordinate plane. Label at least two ordered pairs that are solutions on your graph.
a. 10x+6y=100
b. y=9.5x+20
c. 7x-3y=21
d. y=4(x+10)
Answer:
Solutions are shown below.
Question 3.
Mari and Lori are starting a business to make gourmet toffee. They gather the following information from another business about prices for different amounts of toffee. Which equation and which graph are most likely to model the price, p, for x pounds of toffee? Justify your reasoning.
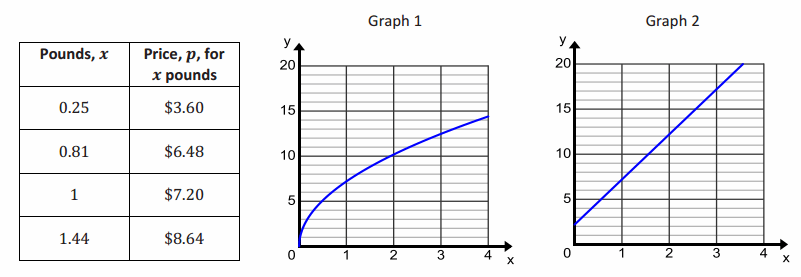
Equation A: p=5x+2.2
Equation B: p=7.2\(\sqrt{x}\)
Answer:
Graph 1 is a nonlinear function. It fits the table data better and seems to be the correct equation. I estimated a few ordered pairs on the graph, and they were close matches to the values in the table. The points on the second graph do not match the table values at all for x-values larger than 1.
Eureka Math Algebra 1 Module 1 Lesson 20 Exit Ticket Answer Key
The Math Club sells hot dogs at a school fundraiser. The club earns $108.00 and has a combination of five-dollar and one-dollar bills in its cash box. Possible combinations of bills are listed in the table below. Complete the table.
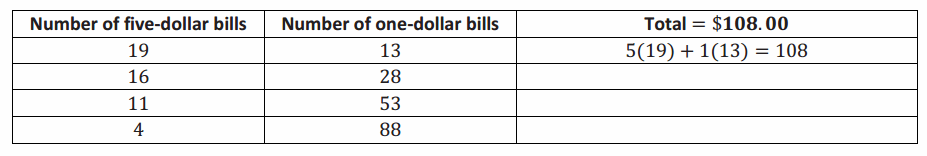
Answer:
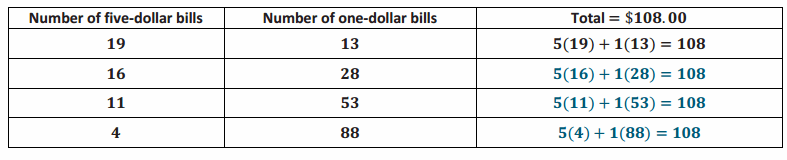
Question 1.
Find one more combination of ones and fives that totals $108.00.
Answer:
(20,8), which stands for 20 fives and 8 ones.
5(20)+1(8)=108
Answer:
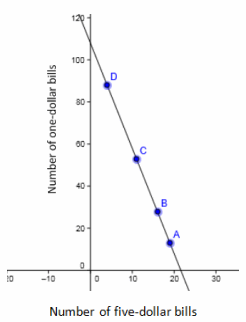
Question 2.
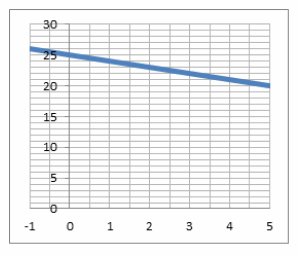
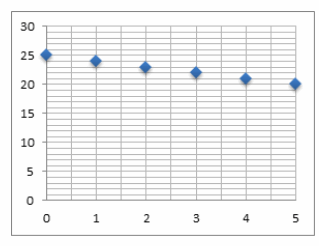
The equation 5x+1y=108 represents this situation. A graph of the line y=-5x+108 is shown. Verify that each ordered pair in the table lies on the line.
Answer:
Graph is shown with points plotted for the solutions. Verify by substituting the ordered pairs in the table into the equation for the line.
Question 3.
What is the meaning of the variables (x and y) and the numbers (1,5, and 108) in the equation 5x+1y=108?
Answer:
x is the number of 5-dollar bills; y is the number of 1-dollar bills; 1 is the value of a 1-dollar bill; 5 is the value of a 5-dollar bill, and 108 is the total dollar amount. If there are x fives, then 5x is the value of all the five-dollar bills.