Engage NY Eureka Math Algebra 1 Module 1 Lesson 14 Answer Key
Eureka Math Algebra 1 Module 1 Lesson 14 Example Answer Key
Example 1.
What is the solution set to the inequality 5q+10>20? Express the solution set in words, in set notation, and graphically on the number line.
Answer:
q can be any value that is more than 2.
q>2
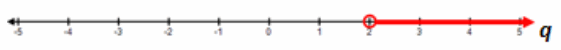
→ Point out to students that these are the only actions that we know do not affect the solution set.
→ Dividing both sides by 5 is still applying the multiplication principle (multiplying both sides by \(\frac{1}{5}\)).
Example 2.
Jojo was asked to solve 6x+12<3x+6, for x. She answered as follows:
6x+12<3x+6
6(x+2)<3(x+2) Apply the distributive property.
6<3 Multiply through by \(\frac{1}{x+2}\).
a. Since the final line is a false statement, she deduced that there is no solution to this inequality (that the solution set is empty).
What is the solution set to 6x+12<3x+6?
Answer:
x<-2
b. Explain why Jojo came to an erroneous conclusion.
Answer:
Multiplying through by \(\frac{1}{x+2}\) is dangerous, as we do not know whether or not \(\frac{1}{x+2}\) is positive or negative (or even well defined). Its value depends on the value one chooses to assign to the variable. We could, potentially, multiply through by a negative value, making the final step invalid. (The property of inequalities allows for only multiplication though by positives.) We do not know, then, if this step is actually valid. Things can, and clearly have, gone wrong.
Example 3.
Solve -q≥-7, for q.
Answer:
-q≥-7
0≥-7+q Add q to both sides.
7≥q Add 7 to both sides.
![]()
Eureka Math Algebra 1 Module 1 Lesson 14 Exercise Answer Key
Exercise 1.
Consider the inequality x2+4x≥5.
a. Sift through some possible values to assign to x that make this inequality a true statement. Find at least two positive values that work and at least two negative values that work.
Answer:
Any value such that x≤-5 or x≥1.
b. Should your four values also be solutions to the inequality x(x+4)≥5? Explain why or why not. Are they?
Answer:
Yes. The inequality can be returned to its original form by using the distributive property, so the two are equivalent.
c. Should your four values also be solutions to the inequality 4x+x2≥5? Explain why or why not. Are they?
Answer:
Yes. The terms on the left-hand side can be rearranged using the commutative property.
d. Should your four values also be solutions to the inequality 4x+x2-6≥-1? Explain why or why not. Are they?
Answer;
Yes. 6 was subtracted from both sides of the inequality. If the same principle of equality holds for inequalities, then the original solutions should still work. (Make sure students confirm this with their answers from (a)).
e. Should your four values also be solutions to the inequality 12x+3x2≥15? Explain why or why not. Are they?
Answer:
Yes. Both sides were multiplied by 3. Using the same multiplication principle of equality, the solution set should not change. (Again, make sure students test this.)
While discussing parts (b) and (c), guide the class discussion to lead to the following conclusion:
→ Just like all our previous work on equations, rewriting an inequality via the commutative, associative, and distributive properties of the real numbers does not change the solution set of that inequality.
Make the point that we are talking about >, <, ≥, and ≤. While discussing (d), point out that it appears we are choosing to accept the addition (and subtraction) property of inequality (if A>B, then A+c>B+c). Students have previously referred to this property as an if-then move.
Ask students to articulate the property as formally as they can; for example, “adding a value to each side of an inequality does not change the solution set of that inequality.”
Conduct a similar discussion to those conducted in Lesson 12. Include the following:
→ Could the solution set to an inequality be changed by applying the commutative, associative, or distributive properties to either side of an inequality?
→ No, the solution set would not change.
→ Could the solution set to an inequality be changed by applying the additive property of inequality?
→ No, the solution set would not change.
While discussing (e), make the same argument for multiplying both sides of an inequality by a positive value:
If A>B, then kA>kB provided k is positive.
This action also does not change the solution set of an inequality.
→ So, if x is a solution to an inequality, it will also be a solution to the new inequality formed when the same number is added to or subtracted from each side of the original inequality or when the two sides of the original inequality are multiplied by the same positive number. This gives us a strategy for finding solution sets.
Exercises 2–3
Exercise 2.
Find the solution set to each inequality. Express the solution in set notation and graphically on the number line.
a. x+4≤7
Answer:
x≤3

b. \(\frac{m}{3}\)+8≠9
Answer:
m≠3

c. 8y+4<7y-2
Answer:
y<-6
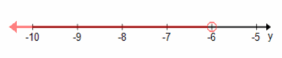
d. 6(x-5)≥30
Answer:
x≥10
![]()
e. 4(x-3)>2(x-2)
Answer:
x>4
![]()
Exercise 3.
Recall the discussion on all the strange ideas for what could be done to both sides of an equation. Let’s explore some of the same issues here but with inequalities. Recall, in this lesson, we have established that adding (or subtracting) and multiplying through by positive quantities does not change the solution set of an inequality. We’ve made no comment about other operations.
a. Squaring: Do B≤6 and B2≤36 have the same solution set? If not, give an example of a number that is in one solution set but not the other.
Answer:
No. In the first inequality, B can equal 6 or any number smaller. The second inequality can only equal numbers from 6 down to -6. For example, B=-7 is not in the solution set.
b. Multiplying through by a negative number: Do 5-C>2 and -5+C>-2 have the same solution set? If not, give an example of a number that is in one solution set but not the other.
Answer:
No. The first inequality has a solution of C<3, and the second has a solution of C>3. The number 4, for example, is a solution to the second but not the first inequality.
c. Bonzo’s ignoring exponents: Do y2<52 and y<5 have the same solution set? Answer: No. When both sides are squared, we end up introducing the possibility that y can be negative but not less than -5. For example, y=-5 is a solution for the second inequality but not the first. → Recall that we have established that making use of the properties of inequalities: If A>B, then A+c>B+c for any real number c.
If A>B, then kA>kB for any positive real number.
Along with all the usual commutative, associative, and distributive properties, to rewrite an inequality does not change the solution set of that inequality.
→ Any action different from these offers no guarantee that your work is yielding valid solutions. These may be candidates you can use to check for solutions, but they must be checked (as we saw in the previous exercise).
→ The next two examples illustrate some more dangers.
Exercises 4–7
Exercise 4.
Find the solution set to each inequality. Express the solution in set notation and graphically on the number line.
a. -2f<-16
Answer:
f>8

b. \(\frac{-x}{12}\)≤\(\frac{1}{4}\)
Answer:
x≥-3
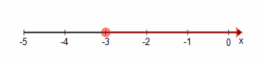
c. 6-a≥15
Answer:
a≤-9
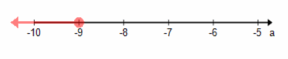
d. -3(2x+4)>0
Answer:
x<-2
![]()
Recall the properties of inequality: → Addition property of inequality: If A>B, then A+c>B+c for any real number c.
→ Multiplication property of inequality:
If A>B, then kA>kB for any positive real number k.
Exercise 5.
Use the properties of inequality to show that each of the following is true for any real numbers p and q.
a. If p≥q, then -p≤-q.
Answer:
p≥q
p-q≥q-q
p-q≥0
p-p-q≥0-p
-q≥-p
b. If p<q, then -5p>-5q.
Answer:
p<q
5p<5q
5p-5p-5q<5q-5p-5q
-5q<-5p -5p>-5q
-p≤-q
c. If p≤q, then -0.03p≥-0.03q.
Answer:
p≤q
0.03p≤0.03q
0.03p-0.03p-0.03q≤0.03q-0.03p-0.03q
-0.03q≤-0.03p
-0.03p≥-0.03q
d. Based on the results from parts (a) through (c), how might we expand the multiplication property of inequality?
Answer:
If A>B, then kA<kB for any negative real number k.
Exercise 6.
Solve -4+2t-14-18t>-6-100t, for t in two different ways: first without ever multiplying through by a negative number and then by first multiplying through by –\(\frac{1}{2}\).
-18-16t>-6-100t
-16t+100t>-6+18
84t>12
t>\(\frac{1}{7}\)
–\(\frac{1}{2}\) (-4+2t-14-18t)<-\(\frac{1}{2}\) (-6-100t)
2-t+7+9t<3+50t
9+8t<3+50t
6<42t
\(\frac{1}{7}\)<t
Exercise 7.
Solve –\(\frac{x}{4}\)+8<\(\frac{1}{2}\), for x in two different ways: first without ever multiplying through by a negative number and then by first multiplying through by -4.
Answer:
–\(\frac{x}{4}\)+8<\(\frac{1}{2}\)
8-\(\frac{1}{2}\)<\(\frac{x}{4}\)
4∙\(\frac{15}{2}\)<4∙\(\frac{x}{4}\)
30-4(\(\frac{1}{2}\))
x-32>-2
x>30
Eureka Math Algebra 1 Module 1 Lesson 14 Problem Set Answer Key
Question 1.
Find the solution set to each inequality. Express the solution in set notation and graphically on the number line.
a. 2x<10
Answer:
{x real | x<5}

b. -15x≥-45
Answer:
{x real | x≤3}

c. \(\frac{2}{3}\) x≠\(\frac{1}{2}\)+2
Answer:
{x real | x≠\(\frac{15}{4}\)}

d. -5(x-1)≥10
Answer:
{x real |x≤-1}

e. 13x<9(1-x)
Answer:
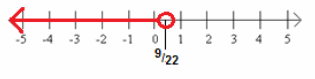
{x real | x<\(\frac{9}{22}\)}
Question 2.
Find the mistake in the following set of steps in a student’s attempt to solve 5x+2≥x+\(\frac{2}{5}\), for x. What is the correct solution set?
5x+2≥x+\(\frac{2}{5}\)
5(x+\(\frac{2}{5}\))≥x+\(\frac{2}{5}\) (factoring out 5 on the left side)
5≥1 (dividing by (x+\(\frac{2}{5}\)))
So, the solution set is the empty set.
Answer:
The third line of the solution is incorrect. Since x is a variable, we do not know whether x+\(\frac{2}{5}\) is positive, negative, or zero. The correct solution to the given problem is x≥-\(\frac{2}{5}\).
Question 3.
Solve –\(\frac{x}{16}\)+1≥-\(\frac{5x}{2}\), for x without multiplying by a negative number. Then, solve by multiplying through by -16.
Answer:
–\(\frac{x}{16}\)+1≥-\(\frac{40x}{16}\)
\(\frac{40x}{16}\)–\(\frac{x}{16}\)≥-1
\(\frac{39x}{16}\)≥-1
x≥-\(\frac{16}{39}\)
-16(-\(\frac{x}{16}\)+1)≤-16(-\(\frac{5x}{2}\))
x-16≤40x
-16≤39x
–\(\frac{16}{39}\)≤x
Question 4.
Lisa brought half of her savings to the bakery and bought 12 croissants for $14.20. The amount of money she brings home with her is more than $2.00. Use an inequality to find how much money she had in her savings before going to the bakery. (Write the inequality that represents the situation, and solve it.)
Answer:
The inequality is 2<\(\frac{x}{2}\)-14.2. The original savings amount must have been more than $32.40.
Eureka Math Algebra 1 Module 1 Lesson 14 Exit Ticket Answer Key
Question 1.
Find the solution set to each inequality. Express the solution in set notation and graphically on the number line.
a. 6x-5<7x+4
Answer:
-5<x+4
-9<x

b. x2+3(x-1)≥x2+5
Answer:
3x-3≥5
3x≥8
x≥\(\frac{8}{3}\)

Question 2.
Fergus was absent for today’s lesson and asked Mike to explain why the solution to -5x>30 is x<-6. Mike said, “Oh! That’s easy. When you multiply by a negative, just flip the inequality.” Provide a better explanation to Fergus about why the direction of the inequality is reversed. Answer: The multiplication property of inequality only applies when multiplying by a positive value. Otherwise, the addition property must be used. 0>5x+30
-30>5x
-6>x
Flipping the direction of the inequality is simply a shortcut for using the addition property.