Domain, Range, and Co-domain are three common terms used in a function. A function relates an input to an output. In simple terms, the domain is the set of values that go into the function, the range is the values that come out of a function, and the codomain is the values that may possibly come out. Let us take a relation F from set A to set B. The relation F is said to be a function if every element of A is mapped with exactly one element of B.
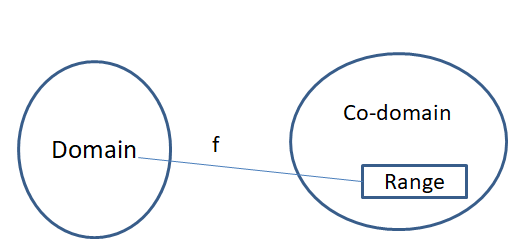
Domain Co-domain and Range of Function
A domain is defined as the set of all values that a function can input while it is defined. The range is all values that come out as output from the function. Co-domain is the set of values that have the potential of coming out as output from the function.
Example:
Suppose the function is f(x) = x³
If the domain is the set of natural numbers.
Domain = {1, 2, 3, 4, 5, . . . }
Range = {1, 8, 27, 64, 125, . . . }
Since it is a function defined from N->N, all natural numbers are potential values that can come out. Hence, the codomain could be the set N.
How to Find Domain & Range of a Function?
The domain can also be defined as the set of possible values for independent variables.
- The independent variables which are allowed are no zero at the denominator of the fraction and no negative sign in the square root function.
- The set of all real numbers are taken as a domain of functions in the form of f(x) = 2x + 5 or x² – 2.
- In some situations, the inerval is specified along with the function like f(x) = 2x + 4, 0 < x < 10. Here x takes the values between 0 and 10 as domian.
- Domain restrictions refer to the values for which the given function cannot be defined.
To Find Range:
After placing the domain, the set of all possibles values comes from the dependent variable. Consider a function y = f(x).
- All possible values of y from minimum to maximum of a domain is the range of the function
- Take the minimum and maximum values of y and then draw a graph.
Differences Between Domain, Co-domain, and Range of a Function
Domain Vs Co-domain
Domain handles with the input values and independent variable in the function while co-domain handles with potential function outputs. And domain deals with x in f(x) and the co-domain tells about the y. The graphical representation is along the lines.
Domain Vs Range
- As we already know that domain is the set of values that are defined on a function and range is the set of all output values of a function.
- While domain associates with the input values of a function, range associates with output.
- In a function f(x), the domain will be all possible values of x, which is the independent variable, on the other hand, range will be the f(x) which is a dependant variable.
Co-domain Vs Range
Actually, the range is the set of values that are coming out of a function by taking certain inputs. And co-domain is the set of possible outcomes of a function.
Also, Read
| Relation | Domain and Range of a Relation |
| Worksheet on Functions or Mapping | Ordered Pair |
| Worksheet on Math Relation |
Questions on Domain Co-domain and Range of a Function
Question 1:
Find domain and range if R is a mapping from A to B.
(i) A = {2, 3, 4}, B = {8, 9, 10}, R = {(2, 9), (3, 10), (4, 8)}
(ii) A = {1, 2, 5, 7, 11}, B = {3, 9, 27} and R = {(1, 3), (2, 9), (5, 9), (7, 3), (11, 27)}
Solution:
(i)
Given that,
A = {2, 3, 4}, B = {8, 9, 10}, R = {(2, 9), (3, 10), (4, 8)}
We can observe that every element in set A has relation with exactly one element of set B. So, R is a mapping from A to B.
Therefore, Domain = {2, 3, 4}, Range = {8, 9, 10}.
(ii)
Given that,
A = {1, 2, 5, 7, 11}, B = {3, 9, 27} and R = {(1, 3), (2, 9), (5, 9), (7, 3), (11, 27)}
The ordered pairs (2, 9), (5, 9) have the same second component, for (1, 3), (7, 3) also have the same component. So, R is not mapping from A to B.
Question 2:
Let N be the set of natural numbers if f: N → N by f (x) = 2x + 5, then find f (2), f (4), f (-1), f (7).
Solution:
Given that,
f (x) = 2x + 5
f (2) = 2(2) + 5
= 4 + 5 = 9
f (4) = 2(4) + 5
= 8 + 5
= 13
f (-1) = 2(-1) + 5
= -2 + 5
= 3
f (7) = 2(7) + 5
= 14 + 5 = 19
Therefore, f (2) = 9, f (4) = 13, f (-1) = 3, and f (7) = 19.
Question 3:
If A = {a, b c, d}, B = {p, q, r, s, t} and f is a function which maps the elements from A to B as shown here. Find domain co-domain and range of function f.
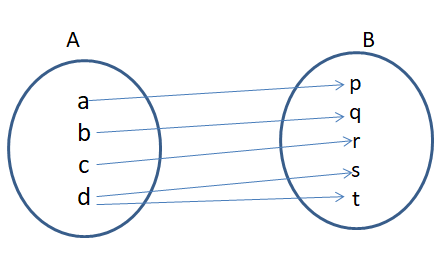
Solution:
Domian of function f = {a, b c, d
Co-domain of function f = {p, , r, s, t}
Range of function f = {p, q, r, s, t}
Question 4:
If A = {11, 12, 13, 14}, B = {15, 16, 17, 18, 19} and
R₁ = {(11, 15), (12, 16), (13, 17)}, R₂ = {(11, 15), (11, 19), (12, 16), (13, 17), (14, 18)}, R₃ = {(11, 15), (12, 16), (13, 17), (14, 18)}
Justify which of the given relation is a function from A to B.
Solution:
Domain for the first relation R₁ is {11, 12, 13} which is not equal to A.
Therefore, R₁ is not a function from A to B.
Two different ordered pairs (11, 15), (11, 19) have the same first component in R₂.
Therefore, R₂ is not a function from A → B.
The domain of the third relation R₃ is {11, 12, 13, 14} is equal to A and no two ordered pairs have the same first component.
Therefore, R₃ is a function from A to B.
