Sets are the collection of well-defined elements. When you try to combine two sets under some conditions to form a new set, it is called a difference of two sets. Moreover, the set difference is one of the operations on sets. By using the set difference, you can just perform operations between only two sets. Check out what is set difference, how to find the difference between two sets, and solved examples in the following sections.
What is meant by Set Difference?
The difference between two sets A and B is represented as A – B. The set difference of A and B is another set that includes the elements A and but not the elements of B. “A – B” can be read as set A minus set B. A – B can also be written as A / B.
Therefore, A – B = {x : x ∈ A and x ∉ B}
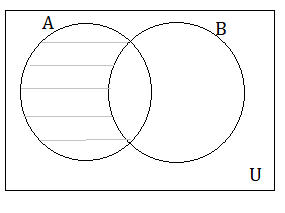
The two important properties of the difference of two sets are
- A – B ≠ B – A
- If A, B are two disjoint sets, then A – B = A and B – A = B.
Also, Read
How to find the Difference of Two Sets?
Follow these simple steps to calculate the difference between the two sets.
- Let us take two sets having well-defined objects of the same type.
- The two sets names can be P and Q.
- In P – Q, you must include the elements of P but not elements of Q.
- Q – P means include elements of Q but not elements of P.
Difference of Two Sets Example Questions and Answers
Example 1:
If A = {25, 5, 50, 23}, B = {1, 5, 10, 20, 25, 50}, then find A – B and B – A.
Solution:
The given two sets are A = {25, 5, 50, 23}, B = {1, 5, 10, 20, 25, 50}
A – B = {25, 5, 50, 23} – {1, 5, 10, 20, 25, 50}
= {23}
B – A = {1, 5, 10, 20, 25, 50} – {25, 5, 50, 23}
= {1, 10, 20}
Therefore, A – B = {23} and B – A = {1, 10, 20}.
Example 2:
If P = {m, n, o, p, q, x, y, z}, Q = {o, p, q, y}
find P – Q and Q – P.
Solution:
The given two sets are P = {m, n, o, p, q, x, y, z}, Q = {w, r, s, t, o, p, q, y}
P – Q means elements of P but not the elements of Q.
P – Q = {m, n, o, p, q, x, y, z} – {w, r, s, t, o, p, q, y}
= {m, n, x, z}
Q – P means the elements of Q but not the elements of P.
Q – P = {w, r, s, t, o, p, q, y} – {m, n, o, p, q, x, y, z}
= {w, r, s, t}
Therefore, P – Q = {m, n, x, z}, Q – P = {w, r, s, t}.
Example 3:
If A = {x : x is a natural number between 10 and 20}, B = {x : x is a even number between 10 and 25} and C = {3, 6, 7, 14, 4, 8}
find B – C, A – B, C – A, A – C, and C – B
Solution:
The given three sets are A = {x : x is a natural number between 10 and 20}, B = {x : x is a even number between 10 and 25} and C = {3, 6, 7, 14, 4, 8}
The roster form of A = {10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
The roster form of B = {10, 12, 14, 16, 18, 20, 22, 24}
B – C = {10, 12, 14, 16, 18, 20, 22, 24} – {3, 6, 7, 14, 4, 8}
= {10, 12, 16, 18, 20, 22, 24}
A – B = {10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20} – {10, 12, 14, 16, 18, 20, 22, 24}
= {11, 13, 15, 17, 19}
C – A = {3, 6, 7, 14, 4, 8} – {10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
= {3, 6, 7, 4 8}
A – C = {10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20} – {3, 6, 7, 14, 4, 8}
= {10, 11, 12, 13, 15, 16, 17, 18, 19, 20}
C – B = {3, 6, 7, 14, 4, 8} – {10, 12, 14, 16, 18, 20, 22, 24}
= {3, 6, 7, 4, 8}
Example 4:
If X = {21, 23, 25}, Y = {32, 34, 36} find X – Y and Y – X
Solution:
The given two sets are X = {21, 23, 25}, Y = {32, 34, 36}
X – Y = {21, 23, 25} – {32, 34, 36}
= {21, 23, 25}
Y – X = {32, 34, 36} – {21, 23, 25}
= {32, 34, 36}
Therefore, X – Y = X and Y – X = Y.
FAQs on Difference of Two Sets
1. What is the difference of set?
The difference between the two sets is denoted as the first set – the second set. While you are evaluating the difference, just include the non common elements of the first set in the result set.
2. How do you subtract two sets?
The subtraction (difference) of two non-empty sets A and B is A – B. A – B = {x : x ∈ A and x ∉ B}. The difference between the two sets means includes the elements of A but not elements of B.
3. How do you solve the complement of sets?
The complement of a set means subtract U and that set. Complement of set B = U – B. Here U is the universal set. The complement of B means the elements of U but not the elements of B.
4. Why A – B is not equal to B – A?
A – B means the elements of A by eliminating the common elements between A and B. B – A means the elements of B by removing the common elements between A and B. So, A – B is not equal to B – A.
