The expanded form which is also known as the expanded notation is the sum of all the place values. Decimal in the expanded form is similar to the integer expanded form. To write the expanded form with decimals first you have to know what is expanded form, place value system, etc. Let us see how to write the expanded form of decimal numbers with different examples.
Do Read:
What is Expanded Form?
Expanded form is a method of writing the number by adding the value of its digits. For better understanding let us expand each of the digits in the place value.
Example: Write expanded form of 2567.
Solution:
The expanded form of 2567 is
2567 – 2× 1000 + 5 × 100 + 6 × 10 + 7 × 1
What is a Decimal Number?
The decimal number system is the standard form for denoting integer and non-integer numbers. Decimals are a short way to write the fractions and mixed fractions. The points placed in the numbers will represent the place value like tenths, hundredths, etc.
Example: Write the decimal 0.5 into a fraction.
Solution:
Here we observe that there is one number after the point.
0.5 can be written as \(\frac{1}{2}\).
Place Value System
A place value system determines the position of the digit in a number. Each digit represents some value in the number, depending upon its position. When a number is represented in the general form, the position of each digit will be expanded like ones, tens, hundreds, and so on.
Decimal in Expanded Form
Decimal in Expanded Form means writing each number according to the place value. It means to multiply each number and write each digit in its given place value and add them all. Learn how to read and write decimals in Expanded form with an example.
Example:
Write the decimal 156.24 in expanded form.
Solution:
Given the number 156.24
We have to write the expanded form with decimals for the number 156.24
156.24 = 1 × 100 + 5 × 10 + 6 × 1 . 2 × \(\frac{1}{10}\) + 4 × \(\frac{1}{100}\)
= 100 + 50 + 6 + \(\frac{2}{10}\) + \(\frac{4}{100}\)
156.24 = 100 + 50 + 6 + 0.2 + 0.04
How to Write Decimal Fractions in Expanded Form?
Learn how to write decimals in expanded form from the below.
1. First take the decimal number.
2. Now write the digits according to the place value.
3. Now multiply the number with the place value and add the digits.
Example:
Write 25.25 decimal in expanded form.
Solution:
25.25 = 2 × tens + 5 × ones + decimal point + 2 × tenths + 5 × hundredths
= 2 × 10 + 5 × 1 . 2 × \(\frac{1}{10}\) + 5 × \(\frac{1}{100}\)
= 20 + 5 + \(\frac{2}{10}\) + \(\frac{5}{100}\)
Examples of Decimals in Expanded Form
Example 1.
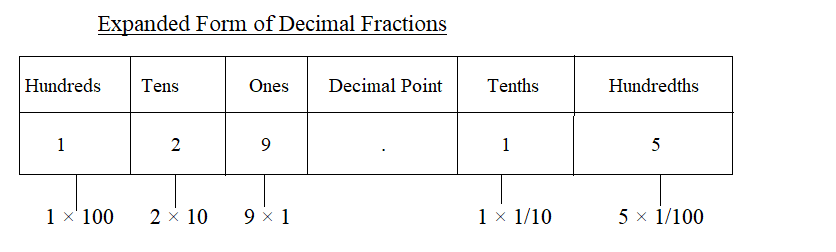
Write the number 129.15 Decimal in Expanded form.
Solution:
First, write the given number 129.15
Write the number according to the place value and multiply the digits.
129.15 = 1 × hundreds + 2 × tens + 9 × ones + decimal point + 1 × tenths + 5 × hundredths
= 1 × 100 + 2 × 10 + 9 × 1 + 1 × \(\frac{1}{10}\) + 5 × \(\frac{1}{100}\)
= 100 + 20 + 9 + \(\frac{1}{10}\) + \(\frac{5}{100}\)
Example 2.
Write the following numbers in Expanded Form of Decimal Fractions
i. 45.12
ii. 4987.56
iii. 961.63
Solution:
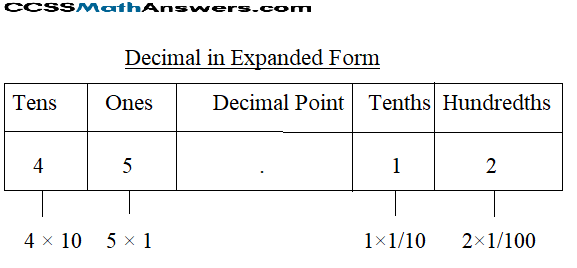
i. 45.12
First, write the given number 45.12
Write the number according to the place value and multiply the digits.
45.12 = 4 × tens + 5 × ones + decimal point + 1 × tenths + 2 × hundredths
45.12 = 4 × 10 + 5 × 1 + 1 × \(\frac{1}{10}\) + 2 × \(\frac{1}{100}\)
45.12 = 40 + 5 + \(\frac{1}{10}\) + \(\frac{2}{100}\)
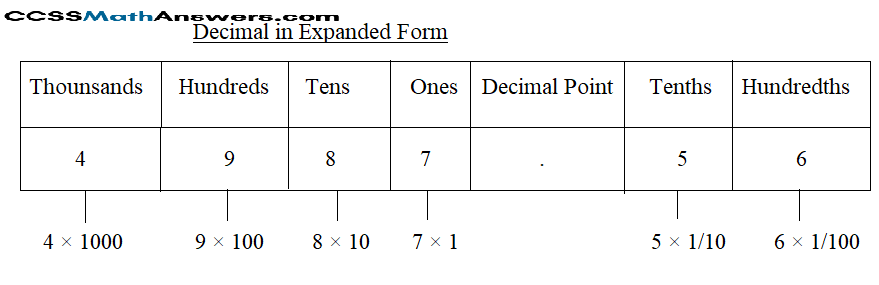
ii. 4987.56
First, write the given number 4987.56
Write the number according to the place value and multiply the digits.
= 4 × thousands + 9 × hundreds + 8 × tens + 7 × ones + decimal point + 5 × tenths + 6 × hundredths
= 4 × 1000 + 9 × 100 + 8 × 10 + 7 × 1 + 5 × \(\frac{1}{10}\) + 6 × \(\frac{1}{100}\)
= 4000 + 900 + 80 + 7 + \(\frac{5}{10}\) + \(\frac{6}{100}\)
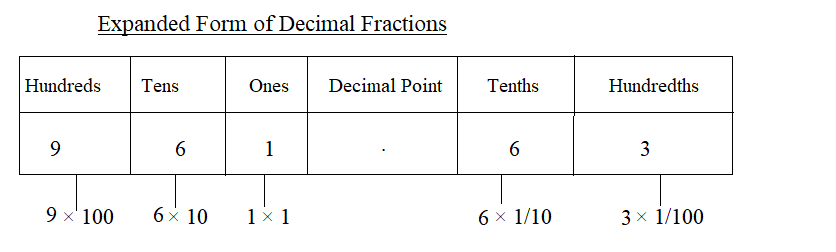
iii. 961.63
First, write the given number 961.63
Write the number according to the place value and multiply the digits.
961.63 = 9 × hundreds + 6 × tens + 1 × ones + decimal point + 6 × tenths + 3 × hundredths
= 9 × 100 + 6 × 10 + 1 × 1 + 6 × \(\frac{1}{10}\) + 3 × \(\frac{1}{100}\)
= 900 + 60 + 6 + \(\frac{6}{10}\) + \(\frac{3}{100}\)
Example 3.
Write the number 70.18 in Expanded form with decimals.
Solution:
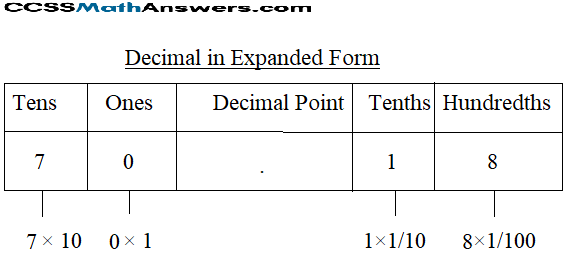
First, write the given number 70.18
Write the number according to the place value and multiply the digits.
70.18 = 7 × tens + 0 × ones + decimal point + 1 × tenths + 8 × hundredths
70.18 = 7 × 10 + 0 × 1 + 1 × \(\frac{1}{10}\) + 8 × \(\frac{1}{100}\)
70.18 = 70 + 0 + \(\frac{1}{10}\) + \(\frac{8}{100}\)
Example 4.
Write Decimals in Expanded form for 111.12
Solution:
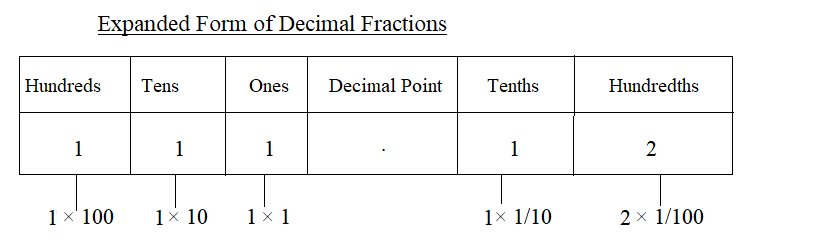
First, write the given number 111.12
Write the number according to the place value and multiply the digits.
111.12= 1 × hundreds + 1 × tens + 1 × ones + decimal point + 1 × tenths + 2 × hundredths
111.12 = 1 × 100 + 1 × 10 + 1 × 1 + 1 × \(\frac{1}{10}\) + 2 × \(\frac{1}{100}\)
111.12 = 100 + 10 + 1 + \(\frac{1}{10}\) + \(\frac{2}{100}\)
Example 5.
Write 1000.42 in Expanded form with decimals.
Solution:
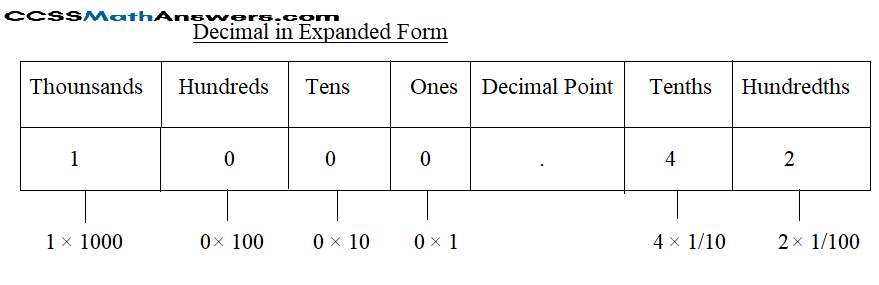
First, write the given number 1000.42
Write the number according to the place value and multiply the digits.
= 1 × thousands + 0 × hundreds + 0 × tens + 0 × ones + decimal point + 4 × tenths + 2 × hundredths
= 1 × 1000 + 0 × 100 + 0 × 10 + 0 × 1 + 4× \(\frac{1}{10}\) + 2 × \(\frac{1}{100}\)
= 1000 + 0 + 0 + 0 + \(\frac{4}{10}\) + \(\frac{2}{100}\)
FAQs on Decimal in Expanded Form
1. How do you write a decimal number in expanded form?
Writing decimals in expanded form simply means writing each number according to its place value. Decimal in Expanded Form is done by multiplying each digit by its place value and adding them together.
2. What is expanded notation with decimals?
The expanded notation for decimals is writing decimal numbers as a sum of each of the digit’s place values.
3. How to write 74.052 in expanded form with decimals?
74.052 in expanded form with decimals can be written as
74.052 = 7 × 10 + 4 × 1 . 0 × \(\frac{1}{10}\) + 5 × \(\frac{1}{100}\) + 2 × \(\frac{1}{1000}\)
= 70 + 4 + 0.0 + 0. 05 + 0.002
