In Math, a decimal number system is a standard system that is the same as the whole number. The whole number part and fraction part is separated by a decimal point. The left side part of the number is the fraction part and the right side part of the number is a whole number part. The concept of the decimal point or number is briefly explained with examples in the coming sections. So, check out this page to know the types of decimals, decimal place values, properties, etc from here.
Read More:
Basic Concept of Decimal
The decimal number system is called the base-ten positional number system. Generally, a decimal numeral refers to the notation of a number in the decimal numeral system. The representation of decimal numbers is known as decimal fractions.
Decimal numbers do not allow the exact representation of the real numbers. Usually, there are two parts in decimal numbers one is the whole number part and the other is the fraction part. And the decimal point or point is represented by (.)
Types of Decimals
The decimal numbers are of three types. They are
1. Recurring Decimal Numbers
2. Non-Recurring Decimal Numbers
3. Decimal Fraction
1. Recurring Decimal Numbers:
Recurring Decimal Numbers are known as Repeating or Non-Terminal Decimals. It consists of finite or infinite numbers.
Example:
3.12 is Finite
3.2454… is Infinite
2. Non-Recurring Decimal Numbers:
Non-Recurring Decimal Numbers are known as Non-Repeating or Terminal Decimals with finite or infinite numbers.
Example:
4.534 is Finite
1.7321…is Infinite
3. Decimal Fraction:
The decimal fraction represents the power of 10. The point means 1 and the numbers after the points will be zeros which are equal to the digits according to the place value.
Example: Convert the decimal 1.23 into the decimal fraction.
Solution:
There are two numbers after the point
The decimal point ‘.’ is equal to 1
‘2’ represents hundredths of positions
‘3’ represents tenths positions
Concept of Decimal Places
The place value represents the position of the digits in a number. The Place values in decimals will determine its value or position. The position of the digit is important in decimals. So, it is necessary to know the place values in decimals.
Example:
Write the place value in decimals for 12.36
Solution:
The position of 1 is the tens place
The position of 2 is the ones place.
The position of 3 is the tenths place
The position of 6 is hundredths place
Properties of Decimals
There are some properties of decimal numbers under arithmetic operations. The properties of decimals are as follows
Property 1:
If a decimal number or fraction is multiplied by 0, the product is 0.
Example: 1.2 × 0 = 0
Property 2.
If a decimal number or fraction is multiplied by 1, the product is the decimal fraction itself.
Example: 1.2 × 1 = 1.2
Property 3:
If any two decimal numbers are multiplied in any order, the product remains the same.
Example: 0.1 × 0.3 = 0.3 × 0.1
Property 4:
If 0 is divided by any decimal number, the quotient will be 0.
Example: 0 ÷ 1.2 = 0
Property 5:
If a decimal number or fraction is divided by 1, the quotient is the decimal number.
Example: 1.2 ÷ 1 = 1.2
Property 6:
If a decimal number or fraction is divided by the same number, then the quotient is 1.
Example: 1.24 ÷ 1.24 = 1
Property 8:
The division of the decimal number or whole number is not possible.
Example: 1.2 ÷ 0 = undefined
Arithmetic Operations on Decimals
Arithmetic Operations are of four types such as addition, subtraction, multiplication, and division. Let us discuss how the arithmetic operations are applicable in decimal numbers with examples.
1. Addition: In decimal numbers, we line up the numbers according to the decimal points and then add the numbers.
Example:
1.2 + 1.2 = 2.4
2. Subtraction: In decimal numbers, we line up the numbers according to the decimal points and then subtract the numbers.
Example: 2.4 – 1.2 = 1.2
3. Multiplication: In multiplication, the numbers will be multiplied by ignoring the decimal points. After the result, we add the decimal points from left to right.
Example: Multiply 6.25 × 2.5
4. Division: In division operations, the decimal points will be shifted from right to left.
Example: 6.26 ÷ 10 = 0.626
Decimal Examples
Example 1.
Add two decimal numbers 17.52 and 14.25
Solution:
First, add the hundredths place
2 + 5 = 7
Now add tenths place value
5 + 2 = 7
Add ones place value
7 + 4 = 11
Put the 1 in ones place and carry 1 to the tens place.
Add tens place value
1 + 1 + 1 = 3
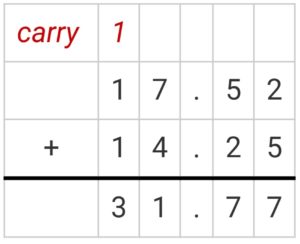
Thus the sum of two decimal numbers 17.52 and 14.25 is 31.77
Example 2.
Multiply the numbers 1.464 and 0.245.
Solution:
There are six decimal places in both numbers.
Ignore the decimal places and then multiply the two given numbers.
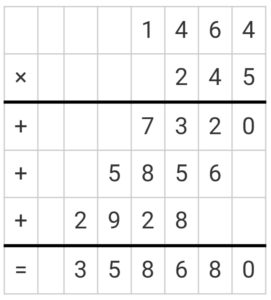
And then rewrite the product by placing six decimal places in the result.
Thus the multiplication of two decimal numbers 1.464 and 0.245 is 0.358680
Example 3.
Convert 3/100 in decimal form.
Solution:
In the fraction 3/100, 3 is the numerator and 100 is the denominator.
Divide 3 by 100.
3 ÷ 100 = 0.03
Here one represents 1 and two zeros represent two numbers after the points.
Example 4.
Write the decimal place value for the highlighted numbers.
i. 12.534
ii. 0.4624
iii. 1.2467
Solution:
i. 12.534
Here we have to write the place value for 4.
4 is placed 3 numbers after the decimal point.
So, the decimal place value is 4 × thousandth = 4 × 1/1000
ii. 0.4624
Here we have to write the place value for 6.
6 is placed two numbers after the decimal point.
So, the decimal place value is 6 × hundredth = 6 × 1/100
iii. 1.2467
Here we have to write the place value for 2.
2 is placed one number after the decimal point.
So, the decimal place value is 2 × tenths = 2 × 1/10
Example 5.
Multiply the two decimal numbers 46.789 with 100.
Solution:
Given the decimal numbers 46.789 and 100.
The concept to use here is multiplying decimal with part 100
We know that,
The decimal point will shift to the right when we multiply with 10, 100, 1000…
Here we have to multiply with 100 which means there are two zeros.
So we have to place the decimal point after the two numbers.
That means 46.789 × 100 = 4678.9
FAQs on Concept of Decimals
1. What is the decimal number?
Decimals are the integer and non-integer numbers which consist of two parts whole numbers and fractions and these are separated by the decimal point.
Example: 1.24 is a decimal number.
2. What are the types of decimals?
There are three types of decimals. They are
i. Recurring decimals(Non-Terminating or Repeating)
ii. Non-Recurring decimals (Terminating or Non-Repeating)
iii. Decimal Fraction
3. What are decimal places?
The position of a digit to the right of the decimal point in a number written in decimal notation.
