A set of a pack of well-defined objects. Those objects are called the elements or members of a set. The complement of a set is nothing but the subtraction of a universal set from any of the given set. The set complement contains the non-common elements of the universal set. Get to know more about the complement of a set, its definition, and the process to calculate the set complement from this page. You can also see the solved examples for a better understanding of the concept.
Complement of a Set – Definition
Complement of a set A is denoted by Ac or A’. The complement of set A means Universal set minus set A. The complement set gets the set of elements in the universal set that are not in set A.
The set builder form of set complement is A’ = {x: x ∈ U and x ∉ A}
The Venn diagram of the complement of a set A is
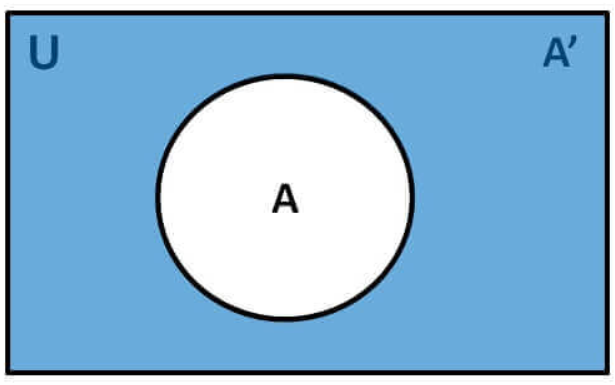
The important points about the set complement are provided here.
- The set and its complement are disjoint sets
- The complement of an empty set is a universal set.
- The complement of a universal set is an empty set.
How to find the Complement of a Set?
Grab the detailed step-by-step explanation on how to calculate the complement of a set from the following sections.
- At first, you need to take two sets universal set and anyone set.
- Set complement = Universal_Set – Given_Set
- In the resultant complement set, you need to write the elements of a universal set that are not elements of the given set.
Properties of Complement Sets
(i) Complement Law
A U A’ = A ‘ U A
(A ∩ B’) = ϕ
(ii) Law of Complementation
(A’)’ = A
(iii) De Morgan’s Law
(A ∩ B’) = ϕ
(A U B) = A’ ∩ B’
(iv) Law of Empty Set
ϕ’ = ∪
(v) Law of Universal Set
∪’ = ϕ
Have a look at the solved example problems on the set complement to get a better idea of the concept easily.
Also, Read
Complement of a Set Examples
Example 1:
If A = {1, 3, 5, 7, 9, 11}, ∪ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, find the complement of A.
Solution:
Given sets are
A = {1, 3, 5, 7, 9, 11}, ∪ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Ac = ∪ – A
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} – {1, 3, 5, 7, 9, 11}
= {2, 4, 6, 8, 10}
Therefore, Ac = {2, 4, 6, 8, 10}
Example 2:
If ∪ = {5, 10, 15, 20, 25, 30, 35}, B = {10, 20, 30, 40, 50, 60}, evaluate the complement of set B.
Solution:
Given sets are
∪ = {5, 10, 15, 20, 25, 30, 35}, B = {10, 20, 30, 40, 50, 60}
B’ = ∪ – B
B’ means include the elements of the universal set that are not in set B.
B’ = {5, 10, 15, 20, 25, 30, 35} – {10, 20, 30, 40, 50, 60}
= {5, 15, 25, 35}
Therefore, B’ = {5, 15, 25, 35}.
Example 3:
If P = {2, 3, 5, 7, 9}, Q = {1, 4, 5, 8, 10}, ∪ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, then prove that (P ∩ Q)’ = P’ ∪ Q’
Solution:
Given sets are
P = {2, 3, 5, 7, 9}, Q = {1, 4, 5, 8, 10}, ∪ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
P’ = ∪ – P
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} – {2, 3, 5, 7, 9}
= {1, 4, 6, 8, 10}
Q’ = ∪ – Q
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} – {1, 4, 5, 8, 10}
= {2, 3, 6, 7, 9}
P ∩ Q = {2, 3, 5, 7, 9} ∩ {1, 4, 5, 8, 10}
= {5}
L.H.S = (P ∩ Q)’
= ∪ – (P ∩ Q)
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} – {5}
= {1, 2, 3, 4, 6, 7, 8, 9, 10}
R.H.S = P’ ∪ Q’
= {1, 4, 6, 8, 10} ∪ {2, 3, 6, 7, 9}
= {1, 2, 3, 4, 6, 8, 7, 9, 10}
L.H.S = R.H.S
Hence, proved.
Example 4:
If A = {l, a, d, r}, ∪ = {a, b, c, d, k, l, r, s t, y}, then show that A ∪ A’ = A’ ∪ A = ∪
Solution:
Given sets are
A = {l, a, d, r}, ∪ = {a, b, c, d, k, l, r, s t, y}
To prove that, A ∪ A’ = A’ ∪ A = ∪
A’ = ∪ – A
= {a, b, c, d, k, l, r, s t, y} – {l, a, d, r}
= {b, c, k, s, t, y}
A ∪ A’ = {l, a, d, r} ∪ {b, c, k, s, t, y}
= {l, a, d, r, b, c, k, s, t, y} = ∪
A’ ∪ A = {b, c, k, s, t, y} ∪ {l, a, d, r}
= {b, c, k, s, t, y, l, a, d, r} = ∪
Hence, shown.
FAQs on Set Complement
1. Which law deals with the complement of a set?
The various laws which deal with the set complement are listed here.
Complement laws (union and intersection) A ∪ A’ = U, A ∩ A’ = ∅
Law of double complementation (A’)’ = A
Law of empty and universal set ∅’ = U, U’ = ∅
De Morgan’s Complement Law (A∪B)’ = A’ ∩ B’, (A ∩ B)’ = A’ ∪ B’
2. How do you solve complements of a set?
The complement of a set is obtained by subtracting the universal set from the given set. The resultant set complement has the set of elements that are in the universal set and not in the given set.
3. What is the symbol of a complement of a set?
The complement of a set M is represented as M’ or Mc.
4. What is a universal set?
A universal set is a set that includes all the elements of other sets, including its own elements. It is represented by ‘U’.
