Unlike Fractions are fractions with different denominators. For example, \(\frac { 4 }{ 3 } \), \(\frac { 2 }{ 5 } \), \(\frac { 1 }{ 9 } \), \(\frac { 3 }{ 41 } \) are some of the examples of unlike fractions. Unequal reactions are completely different from like fractions where the denominator is the same for the like fractions.
Compared to like fractions, it is difficult to perform arithmetic operations on unlike fractions. So, we need to follow some methods to resolve unlike fractions while performing arithmetic operations and Comparing Unlike Fractions. Check out the complete methods and processes to compare unlike fractions in this article. Also, find out all the 6th Grade Math concepts on our website for better preparation.
Also, find:
How to Compare Unlike Fractions with LCM?
Follow the below process to compare unlike fractions. The step-by-step method is given below with a detailed explanation.
Step 1: Firstly, convert the Unlike fractions into like fractions.
Step 2: Take the LCM of given unlike fractions where LCM is the least common multiple.
Step 3: Now, we can see each fraction that consists of an equivalent fraction with the same denominator having the obtained LCM.
Step 4: Now, all the denominators appear similar. We need to compare the numerators having large numbers.
Step 5: Note down the large number and finalize the large and small fractions.
How to Compare Fractions if Denominators are Different?
Check out the below problems and know the complete concept of comparing unlike fractions.
Question 1:
Which is larger \(\frac { 3 }{ 2 } \) or \(\frac { 5 }{ 6 } \)?
Solution:
Given fractions are \(\frac { 3 }{ 2 } \) and \(\frac { 5 }{ 6 } \)
- To compare the given fractions, first, we need to find the equivalent fractions with a common denominator. Then rearrange the fractions with the help of their numerators.
- The fractions \(\frac { 3 }{ 2 } \) and \(\frac { 5 }{ 6 } \) consists the denomiators as 2 and 6.
- The LCM or common denominator of 2 and 6 is 6.
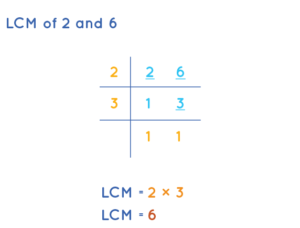
- Now, multiply the fraction \(\frac { 3 }{ 2 } \) with 3 on top and bottom. \(\frac { 9 }{ 6 } \)
- Next, multiply the fraction \(\frac { 5 }{ 6 } \) with 1 on top and bottom. \(\frac { 5 }{ 6 } \)
- Now, both fractions are converted to like fractions.
- Compare the top numbers of the fractions to find out the large fraction. The top numbers of the fractions are 9 and 5.
- 9 is greater than 5.
Therefore, \(\frac { 3 }{ 2 } \) is greater than \(\frac { 5 }{ 6 } \).
Question 2:
Which is larger \(\frac { 7 }{ 4 } \) or \(\frac { 5 }{ 3 } \)?
Solution:
Given fractions are \(\frac { 7 }{ 4 } \) and \(\frac { 5 }{ 3 } \)
- To compare the given fractions, first, we need to find the equivalent fractions with a common denominator. Then rearrange the fractions with the help of their numerators.
- The fractions \(\frac { 7 }{ 4 } \) and \(\frac { 5 }{ 3 } \) consists the denomiators as 4 and 3.
- The LCM or common denominator of 4 and 3 is 12.

- Now, multiply the fraction \(\frac { 7 }{ 4 } \) with 3 on top and bottom. \(\frac { 21 }{ 12 } \)
- Next, multiply the fraction \(\frac { 5 }{ 3 } \) with 4 on top and bottom. \(\frac { 20 }{ 12 } \)
- Now, both fractions are converted to like fractions.
- Compare the top numbers of the fractions to find out the large fraction. The top numbers of the fractions are 21 and 20.
- 21 is greater than 20.
Therefore, \(\frac { 7 }{ 4 } \) is greater than \(\frac { 5 }{ 3 } \).
Question 3:
Arrange the fractions \(\frac { 5 }{ 4 } \), \(\frac { 5 }{ 3 } \), \(\frac { 7 }{ 2 } \), \(\frac { 6 }{ 5 } \) in ascending order.
Solution:
Given fractions are \(\frac { 5 }{ 4 } \), \(\frac { 5 }{ 3 } \), \(\frac { 7 }{ 2 } \), and \(\frac { 6 }{ 5 } \).
- To compare the given fractions, first, we need to find the equivalent fractions with a common denominator. Then rearrange the fractions with the help of their numerators.
- The fractions \(\frac { 5 }{ 4 } \), \(\frac { 5 }{ 3 } \), \(\frac { 7 }{ 2 } \), and \(\frac { 6 }{ 5 } \) consists the denomiators as 2, 3, 4 and 5.
- The LCM or common denominator of 2, 3, 4, and 5 is 60.
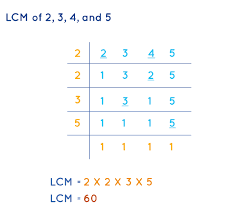
- Now, multiply the fraction \(\frac { 5 }{ 4 } \) with 15 on top and bottom. \(\frac { 75 }{ 60 } \).
- Next, multiply the fraction \(\frac { 5 }{ 3 } \) with 20 on top and bottom. \(\frac { 100 }{ 60 } \).
- Then, multiply the fraction \(\frac { 7 }{ 2 } \) with 30 on top and bottom. \(\frac { 210 }{ 60 } \).
- Next, multiply the fraction \(\frac { 6 }{ 5 } \) with 12 on top and bottom. \(\frac { 72 }{ 60 } \).
- Now, both fractions are converted to like fractions.
- Compare the top numbers of the fractions to find out the small and large fractions. The top numbers of the fractions are 210, 100, 75, and 72.
- 72 < 75 < 100 < 210.
Therefore, \(\frac { 6 }{ 5 } \), \(\frac { 5 }{ 4 } \), \(\frac { 5 }{ 3 } \), and \(\frac { 7 }{ 2 } \) is the ascending order of given fractions.
Question 4:
Arrange the following fractions in descending order \(\frac { 3 }{ 4 } \), \(\frac { 5 }{ 3 } \), 1, \(\frac { 2 }{ 3 } \), and \(\frac { 6 }{ 4 } \).
Solution:
Given fractions are \(\frac { 3 }{ 4 } \), \(\frac { 5 }{ 3 } \), 1, \(\frac { 2 }{ 3 } \), and \(\frac { 6 }{ 4 } \).
- To compare the given fractions, first, we need to find the equivalent fractions with a common denominator. Then rearrange the fractions with the help of their numerators.
- The fractions \(\frac { 3 }{ 4 } \), \(\frac { 5 }{ 3 } \), 1, \(\frac { 2 }{ 3 } \), and \(\frac { 6 }{ 4 } \) consists the denomiators in common as 1, 4 and 3.
- The LCM or common denominator of 1, 4, and 3 is 12.

- Now, multiply the fraction \(\frac { 3 }{ 4 } \) with 3 on top and bottom. \(\frac { 9 }{ 12 } \)
- Next, multiply the fraction \(\frac { 5 }{ 3 } \) with 4 on top and bottom. \(\frac { 20 }{ 12 } \)
- Then, multiply the number 1 with 12 on top and bottom. \(\frac { 12 }{ 12 } \).
- Also, multiply the fraction \(\frac { 2 }{ 3 } \) with 4 on top and bottom. \(\frac { 8 }{ 12 } \)
- Multiply the fraction \(\frac { 6 }{ 4 } \) with 3 on top and bottom. \(\frac { 18 }{ 12 } \)
- Now, both fractions are converted to like fractions.
- Compare the top numbers of all the fractions to find out the small and large fractions. The top numbers of the fractions are 9, 20, 12, 8, and 18.
- 20 > 18 > 12 > 9 > 8.
Therefore, \(\frac { 5 }{ 3 } \), \(\frac { 6 }{ 4 } \), 1, \(\frac { 3 }{ 4 } \), and \(\frac { 2 }{ 3 } \) is the descending order of given fractions.
Converting Unlike Fractions to Like Fractions
It is important to convert the unlike fractions to like fractions to compare them. You can generally follow two methods to compare unlike fractions to like fractions. Check out the below example to know how to convert and compare unlike fractions by converting them to like fractions.
Comparing Fractions with Unlike Denominators Examples
Example 1.
Compare \(\frac { 7 }{ 6 } \) and \(\frac { 5 }{ 9 } \).
Solution: Method 1: Convert the given unlike fractions into like fractions.
To convert the unlike fractions into like fractions, find the LCM of the denominators of the given fractions.
LCM of denominators 6 and 9 is 18.
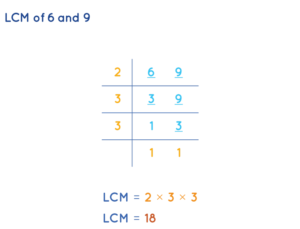
Now, multiply the fraction \(\frac { 7 }{ 6 } \) with 3 on top and bottom. \(\frac { 21 }{ 18 } \). Next, multiply the fraction \(\frac { 5 }{ 9 } \) with 2 on top and bottom. \(\frac { 10 }{ 18 } \).
Now, both fractions are converted to like fractions.
As both the denominators are equal now, you can compare the numerators to find the largest and smallest number.
\(\frac { 21 }{ 18 } \) > \(\frac { 10 }{ 18 } \).
So, \(\frac { 7 }{ 6 } \) > \(\frac { 5 }{ 9 } \).
Method 2: We can also use cross multiplication to convert the unlike fractions to like fractions.
So, firstly take the given fractions. The given fractions are \(\frac { 7 }{ 6 } \) and \(\frac { 5 }{ 9 } \).
Now, cross multiply the given fractions.
7 × 9 = 63; 6 × 5 = 30.
63 > 30.
Therefore, \(\frac { 7 }{ 6 } \) is greater than \(\frac { 5 }{ 9 } \).
Comparing Unlike Fractions Solved Examples
Question 1.
Compare the given fractions by putting the right sign <, > or =.
(i) \(\frac { 2 }{ 5 } \) ___ \(\frac { 2 }{ 11 } \)
(ii) \(\frac { 7 }{ 3 } \) ___ \(\frac { 8 }{ 3 } \)
(iii) \(\frac { 3 }{ 9 } \) ___ \(\frac { 6 }{ 15 } \)
(iv) \(\frac { 4 }{ 3 } \) ___ \(\frac { 3 }{ 2 } \)
(v) 1 ___ 1
(vi) \(\frac { 10 }{ 5 } \) ___ \(\frac { 10 }{ 7 } \)
(vii) \(\frac { 5 }{ 3 } \) ___ \(\frac { 12 }{ 9 } \)
(viii) \(\frac { 20 }{ 15 } \) ___ \(\frac { 28 }{ 21 } \)
(ix) \(\frac { 4 }{ 7 } \) ___ \(\frac { 10 }{ 13 } \)
Solution:
(i) Given fractions are \(\frac { 2 }{ 5 } \) and \(\frac { 2 }{ 11 } \).
LCM of 5 and 11 is 55.
Now, the fraction becomes \(\frac { 22 }{ 55 } \) and \(\frac { 10 }{ 55 } \).
22 > 10. So the answer is >.
\(\frac { 2 }{ 5 } \) > \(\frac { 2 }{ 11 } \)
(ii) Given fractions are \(\frac { 7 }{ 3 } \) and \(\frac { 8 }{ 3 } \).
Both the denominators are the same. So, now compare the numerators.
7 < 3. So the answer is <.
\(\frac { 7 }{ 3 } \) < \(\frac { 8 }{ 3 } \).
(iii) Given fractions are \(\frac { 3 }{ 9 } \) and \(\frac { 6 }{ 15 } \).
LCM of 9 and 15 is 45.
Now, the fraction becomes \(\frac { 15 }{ 45 } \) and \(\frac { 18 }{ 45 } \).
15 < 18. So the answer is <.
\(\frac { 3 }{ 9 } \) < \(\frac { 6 }{ 15 } \)
(iv) Given fractions are \(\frac { 4 }{ 3 } \) and \(\frac { 3 }{ 2 } \).
LCM of 3 and 2 is 6.
Now, the fraction becomes \(\frac { 8 }{ 6 } \) and \(\frac { 9 }{ 6 } \).
8 < 9. So the answer is <.
\(\frac { 4 }{ 3 } \) < \(\frac { 3 }{ 2 } \).
(v) Given numbers are 1 and 1. So the answer is =.
1 = 1.
(vi) Given fractions are \(\frac { 10 }{ 5 } \) and \(\frac { 10 }{ 7 } \).
LCM of 5 and 7 is 35.
Now, the fraction becomes \(\frac { 70 }{ 35 } \) and \(\frac { 50 }{ 35 } \).
70 > 50. So the answer is >.
\(\frac { 10 }{ 5 } \) > \(\frac { 10 }{ 7 } \).
(vii) Given fractions are \(\frac { 5 }{ 3 } \) and \(\frac { 12 }{ 9 } \).
LCM of 3 and 9 is 9.
Now, the fraction becomes \(\frac { 15 }{ 9 } \) and \(\frac { 12 }{ 9 } \).
15 > 12. So the answer is >.
\(\frac { 15 }{ 9 } \) > \(\frac { 12 }{ 9 } \).
(viii) Given fractions are \(\frac { 20 }{ 15 } \) and \(\frac { 28 }{ 21 } \).
LCM of 15 and 21 is 105.
Now, the fraction becomes \(\frac { 140 }{ 105 } \) and \(\frac { 140 }{ 105 } \).
140 = 140. So the answer is =.
\(\frac { 20 }{ 15 } \) = \(\frac { 28 }{ 21 } \).
(ix) Given fractions are \(\frac { 4 }{ 7 } \) and \(\frac { 10 }{ 13 } \).
LCM of 7 and 13 is 91.
Now, the fraction becomes \(\frac { 52 }{ 91 } \) and \(\frac { 70 }{ 91 } \).
52 < 70. So the answer is <.
\(\frac { 4 }{ 7 } \) < \(\frac { 10 }{ 13 } \).
2. Arrange the given fractions in ascending order.
(i) \(\frac { 9 }{ 6 } \), \(\frac { 9 }{ 8 } \), \(\frac { 9 }{ 4 } \)
(ii) \(\frac { 1 }{ 8 } \), \(\frac { 1 }{ 2 } \), 1
(iii) \(\frac { 3 }{ 2 } \), \(\frac { 9 }{ 4 } \), \(\frac { 15 }{ 8 } \)
(iv) \(\frac { 4 }{ 5 } \), \(\frac { 6 }{ 5 } \), \(\frac { 6 }{ 4 } \)
Solution: (i) Given fractions are \(\frac { 9 }{ 6 } \), \(\frac { 9 }{ 8 } \), and \(\frac { 9 }{ 4 } \).
LCM of 6, 8, and 4 is 24.
Now, the fractions becomes \(\frac { 36 }{ 24 } \), \(\frac { 27 }{ 24 } \), and \(\frac { 54 }{ 24 } \).
27 < 36 < 54.
Therefore, \(\frac { 9 }{ 8 } \), \(\frac { 9 }{ 6 } \), and \(\frac { 9 }{ 4 } \) is the ascending order of given fractions.
(ii) Given fractions are \(\frac { 1 }{ 8 } \), \(\frac { 1 }{ 2 } \), and 1.
LCM of 8, 2, and 1 is 8.
Now, the fractions becomes \(\frac { 1 }{ 8 } \), \(\frac { 4 }{ 8 } \), and \(\frac { 8 }{ 8 } \).
1 < 4 < 8.
Therefore, \(\frac { 1 }{ 8 } \), \(\frac { 1 }{ 2 } \), and 1 is the ascending order of given fractions.
(iii) Given fractions are \(\frac { 3 }{ 2 } \), \(\frac { 9 }{ 4 } \), and \(\frac { 15 }{ 8 } \).
LCM of 2, 4, and 8 is 8.
Now, the fractions becomes \(\frac { 12 }{ 8 } \), \(\frac { 18 }{ 8 } \), and \(\frac { 15 }{ 8 } \).
12 < 15 < 18.
Therefore, \(\frac { 3 }{ 2 } \), \(\frac { 15 }{ 8 } \), and \(\frac { 9 }{ 4 } \) is the ascending order of given fractions.
(iv) Given fractions are \(\frac { 4 }{ 5 } \), \(\frac { 6 }{ 5 } \), \(\frac { 6 }{ 4 } \).
LCM of 4, and 5 is 20.
Now, the fractions becomes \(\frac { 16 }{ 20 } \), \(\frac { 24 }{ 20 } \), and \(\frac { 30 }{ 20 } \).
16 < 24 < 30.
Therefore, \(\frac { 4 }{ 5 } \), \(\frac { 6 }{ 5 } \), \(\frac { 6 }{ 4 } \) is the ascending order of given fractions.
Word Problems on Comparing Unlike Fractions
Question 1.
Sam ate \(\frac { 3 }{ 18 } \) part of the chocolate and Sophia ate \(\frac { 5 }{ 9 } \) part of the chocolate. Who ate the greater part of the chocolate? What fraction of chocolate was finished by the two girls?
Solution:
Given that Sam ate \(\frac { 3 }{ 18 } \) part of the chocolate and Sophia ate \(\frac { 5 }{ 9 } \) part of the chocolate.
Firstly, take the fractions and convert them into like fractions.
LCM of 9 and 18 is 18.
So, \(\frac { 3 }{ 18 } \) and \(\frac { 10 }{ 18 } \) are the like fractions now.
Compare the two fractions \(\frac { 3 }{ 18 } \) and \(\frac { 10 }{ 18 } \).
As 10 is greater than 3, \(\frac { 5 }{ 9 } \) is greater than \(\frac { 3 }{ 18 } \). Sophia ate a greater part of the chocolate.
Now, add two fractions to find the chocolate finished by the two girls.
\(\frac { 3 }{ 18 } \) + \(\frac { 5 }{ 9 } \) = \(\frac { 3 + 10 }{ 18 } \) = \(\frac { 13 }{ 18 } \).
\(\frac { 13 }{ 18 } \) fraction of chocolate was finished by the two girls.
Question 2.
Ram traveled \(\frac { 10 }{ 6 } \) km of distance in a car and alex traveled \(\frac { 6 }{ 4 } \) km of distance in a car. Who covered the greater distance?
Solution:
Given that Ram traveled \(\frac { 10 }{ 6 } \) km of distance in a car and alex traveled \(\frac { 6 }{ 4 } \) km of distance in a car.
Firstly, take the fractions and convert them into like fractions.
LCM of 6 and 4 is 12.
So, \(\frac { 20 }{ 12 } \) and \(\frac { 18 }{ 12 } \) are the like fractions now.
Compare the two fractions \(\frac { 20 }{ 12 } \) and \(\frac { 18 }{ 12 } \).
As 20 is greater than 18, \(\frac { 10 }{ 6 } \) is greater than \(\frac { 6 }{ 4 } \).
Therefore, Ram traveled more distance compared to Alex.
Question 3.
Yash walked for \(\frac { 62 }{ 4 } \) km and William walked for \(\frac { 27 }{ 2 } \) km during the weekend. Who cycled more and by how much?
Solution:
Given that Yash walked for \(\frac { 62 }{ 4 } \) km and William walked for \(\frac { 27 }{ 2 } \) km during the weekend.
Firstly, take the fractions and convert them into like fractions.
LCM of 2 and 4 is 4.
So, \(\frac { 62 }{ 4 } \) and \(\frac { 54 }{ 4 } \) are the like fractions now.
Compare the two fractions \(\frac { 62 }{ 4 } \) and \(\frac { 54 }{ 4 } \).
As 62 is greater than 54, \(\frac { 62 }{ 4 } \) is greater than \(\frac { 27 }{ 2 } \).
\(\frac { 62 }{ 4 } \) – \(\frac { 27 }{ 2 } \) = 2
Therefore, Yash walked more compared to William. Yash walked 2km more than William.
Frequently Asked Questions and Answers
Question 1. What are unlike fractions?
Answer: Unlike fractions are the fractions with different denominators. So, the fractions with different denominators like 3, 4, and 5 are called unlike fractions.
Question 2. What is the unlike fraction example?
Answer: The example of unlike fraction is \(\frac { 4 }{ 3 } \), \(\frac { 3 }{ 5 } \), etc.
Question 3. What are the methods to compare unlike fractions?
Answer: You can use two methods to compare unlike fractions. They are
(i) Converting unlike fractions to like fractions.
(ii) Cross multiplication of the fractions to compare unlike fractions.
Question 4. How do you compare unlike fractions with LCM?
Answer: We can compare unlike fractions with LCM.
Firstly, take the LCM of given fraction denominators.
Then, convert the fraction according to the obtained LCM.
Then, finally, compare the fraction depending on the largest number by comparing the numerators of the given fractions.
Question 5. What is the difference between like fraction and unlike fraction?
Answer: The main difference between like fraction and unlike fraction is the like fraction consists of the same denominator where the unlike fraction consists of the different denominator.
