Students looking for the Bridges in Mathematics Grade 5 Student Book Answer Key Unit 5 Module 2 can find a better approach to solve the problems.
Bridges in Mathematics Grade 5 Student Book Answer Key Unit 5 Module 2
Bridges in Mathematics Grade 5 Student Book Unit 5 Module 2 Session 1 Answer Key
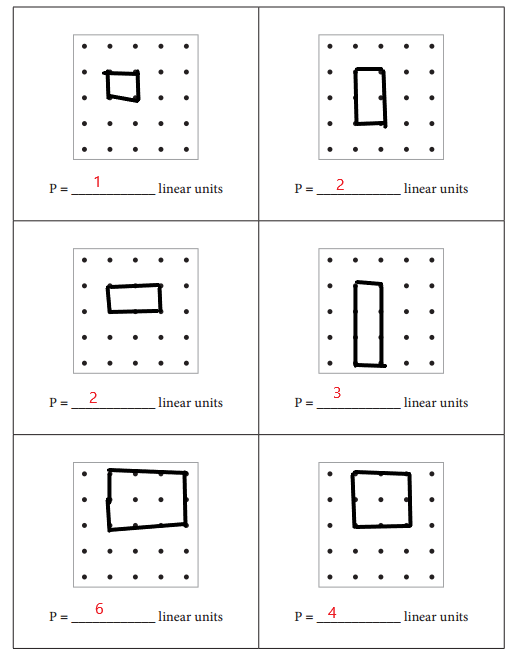
More Geoboard Perimeters
Answer:
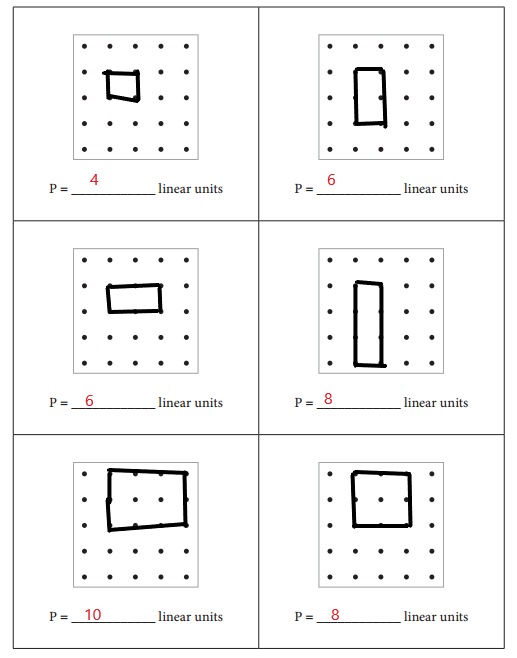
More Geoboard Perimeters, Challenge

Answer:
Reviewing the Standard Algorithm for Multiplication
Question 1.
Solve these multiplication problems.

Answer: 
80 x 60 = 4800
80 x 70 = 5600
80 x 80 = 6400
600 x 10 = 6000
600 x 20 = 12000
600 x 30= 18000
Question 2.
Solve these multiplication problems using the standard algorithm. Use the answers above to make sure your answers are reasonable.
ex:
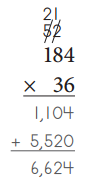
a.
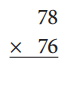
Answer: 5928
78
x 76
———
468
+5460
———
5928
b.
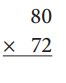
Answer:5760
80
x 72
———–
160
+5600
————–
5760
c.
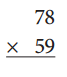
Answer: 4602
78
x 59
——–
702
+3900
———
4602
d.
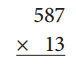
Answer: 7631
587
x 13
————
1761
+ 5870
———–
7631
e.
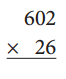
Answer: 15652
602
x 26
———-
3612
+ 12040
—————-
15652
Bridges in Mathematics Grade 5 Student Book Unit 5 Module 2 Session 2 Answer Key
Fraction Multiplication Grids

Simplifying Fractions
Question 1.
Write all the factors of each number below. Try to think of the factors in pairs.

Answer: 
Factors of 2 : 1,2
Factors of 4: 1, 2, 4
Factors of 8: 1, 2. 4, 8
Factors of 3: 1, 3
Factors of 6: 1, 2, 3, 6
Factors of 12: 1, 2, 3, 4, 6, 12
Question 2.
You can simplify a fraction by dividing the numerator and the denominator by the same number. If you divide the numerator and denominator by the largest factor they have in common (the greatest common factor), you can show the fraction in its simplest form. Look carefully at the example below. Then fill in the rest of the table.
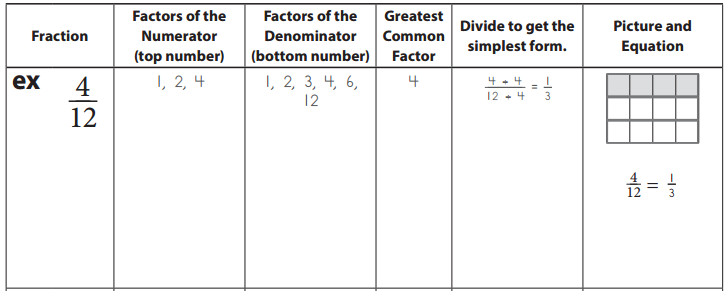
a.
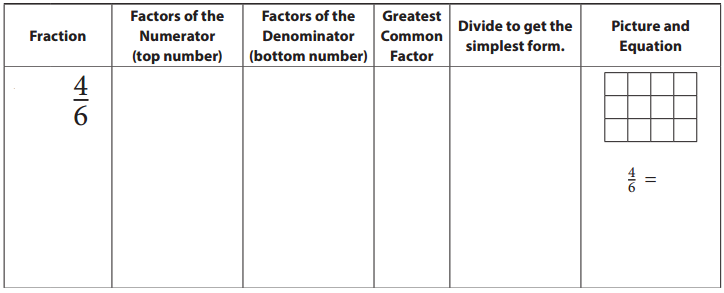
Answer: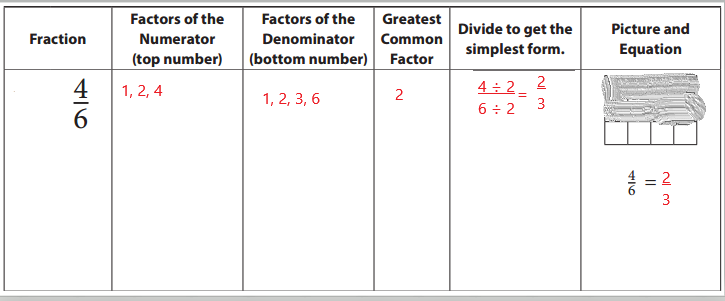
b.
Answer: 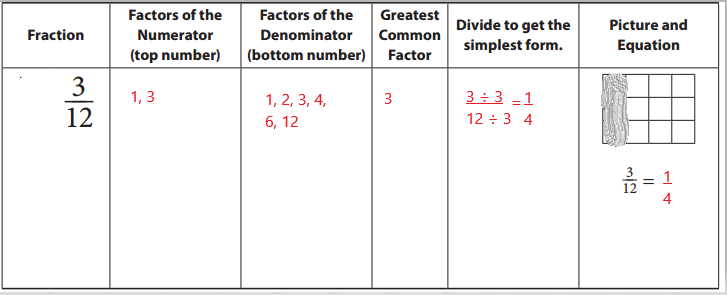
Bridges in Mathematics Grade 5 Student Book Unit 5 Module 2 Session 3 Answer Key
Area of the Addition Key
Question 1.
Julissa measured the + key on her calculator. It was \(\frac{1}{2}\) inch tall and \(\frac{1}{4}\) inch wide. What is the area of the + key?
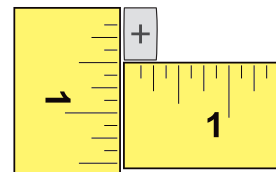
a. Use your geoboard to make a model of the key. In the model, the total area of the geoboard represents 1 square inch, so each side would be exactly 1 inch long.
Answer:
+ key on her calculator was \(\frac{1}{2}\) inch tall and \(\frac{1}{4}\) inch wide.
\(\frac{1}{2}\) = \(\frac{2}{4}\)
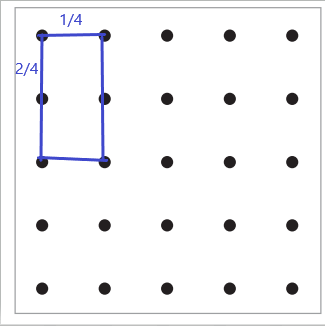
b. Draw a sketch of the geoboard model of the key here. Label the dimensions and area of the key.

Answer:
The + key was drawn by considering the above values.
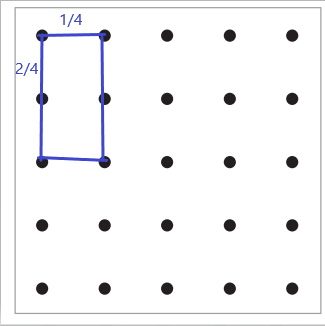
c. Write an equation to show the dimensions and area of the + key on Julissa’s calculator.
Answer: \(\frac{1}{8}\)
+ key on her calculator was \(\frac{1}{2}\) inch tall and \(\frac{1}{4}\) inch wide.
Area = \(\frac{1}{2}\) x \(\frac{1}{4}\)
= \(\frac{1}{8}\)
Multiplying Fractions with the Area Model
Question 1.
For each problem, make a sketch, label the dimensions and area, and write an equation.
a. There was a price tag on Isabel’s new book that was 4 inch wide and 4 inch long. What was the area of the price tag?

Answer: area = 16 square inches

width = 4 inch
long = 4 inch
area = width x long
area = 4 x 4
area = 16 square inches
b. Tomas’s teacher has little stickers she likes to give out when her students have had a good day. Each sticker is \(\frac{1}{2}\) inch wide and \(\frac{1}{2}\) inch tall. What is the area of each sticker?

Answer: area = \(\frac{1}{4}\) square inches

width = \(\frac{1}{2}\)
long = \(\frac{1}{2}\)
area = width x long
area = \(\frac{1}{2}\) x \(\frac{1}{2}\)
area = \(\frac{1}{4}\)
c. There is a special holiday stamp that measures \(\frac{3}{4}\) inch by \(\frac{1}{2}\) inch. What is the area of the stamp?

Answer: area = \(\frac{3}{8}\) square inches

area = \(\frac{3}{4}\) x \(\frac{1}{2}\)
area = \(\frac{3}{8}\)
Question 2.
For each multiplication problem, draw an array, label the dimensions and area, and write an equation.
a. \(\frac{1}{2}\) × \(\frac{1}{8}\)

Answer: \(\frac{1}{16}\)

\(\frac{1}{2}\) x \(\frac{1}{8}\) = \(\frac{1}{16}\)
b. \(\frac{5}{8}\) × \(\frac{1}{4}\)

Answer: \(\frac{5}{32}\)

\(\frac{5}{8}\) × \(\frac{1}{4}\) = \(\frac{5}{32}\)
Question 3.
Choose two fractions and show how you could multiply them on this grid. Label the dimensions and area, and write an equation to show the fractions and their product.

Answer:

\(\frac{5}{8}\) × \(\frac{1}{4}\) = \(\frac{5}{32}\)
Missing Fractions
Question 1.
Fill in the missing fraction or mixed number in each equation.
1\(\frac{3}{4}\) + ![]() = 2
= 2
1 = \(\frac{2}{5}\) + ![]()
2 = \(\frac{7}{8}\) + ![]()
3 = ![]() + 1\(\frac{4}{5}\)
+ 1\(\frac{4}{5}\)
4 = 1\(\frac{2}{6}\) + ![]()
2\(\frac{3}{5}\) + ![]() = 4\(\frac{2}{10}\)
= 4\(\frac{2}{10}\)
Answer: 1\(\frac{3}{4}\) + \(\frac{1}{4}\) = 2
1 = \(\frac{2}{5}\) + \(\frac{3}{5}\)
2 = \(\frac{7}{8}\) + \(\frac{9}{8}\)
3 = \(\frac{6}{5}\) + 1\(\frac{4}{5}\)
4 = 1\(\frac{2}{6}\) + \(\frac{16}{6}\)
2\(\frac{3}{5}\) + \(\frac{16}{10}\) = 4\(\frac{2}{10}\)
Explanation: 1\(\frac{3}{4}\) + ![]() = 2
= 2
![]() = 2 – 1\(\frac{3}{4}\)
= 2 – 1\(\frac{3}{4}\)
![]() = \(\frac{1}{4}\)
= \(\frac{1}{4}\)
Therefore, 1\(\frac{3}{4}\) + \(\frac{1}{4}\) = 2
1 = \(\frac{2}{5}\) + ![]()
1 – \(\frac{2}{5}\) = ![]()
![]() = \(\frac{3}{5}\)
= \(\frac{3}{5}\)
1 = \(\frac{2}{5}\) + \(\frac{3}{5}\)
2 = \(\frac{7}{8}\) + ![]()
2 – \(\frac{7}{8}\) = ![]()
\(\frac{9}{8}\) = ![]()
2 = \(\frac{7}{8}\) + \(\frac{9}{8}\)
3 = ![]() + 1\(\frac{4}{5}\)
+ 1\(\frac{4}{5}\)
3 – 1\(\frac{4}{5}\) = ![]()
\(\frac{6}{5}\) = ![]()
3 = \(\frac{6}{5}\) + 1\(\frac{4}{5}\)
4 = 1\(\frac{2}{6}\) + ![]()
4 – 1\(\frac{2}{6}\) = ![]()
\(\frac{16}{6}\) = ![]()
4 = 1\(\frac{2}{6}\) + \(\frac{16}{6}\)
2\(\frac{3}{5}\) + ![]() = 4\(\frac{2}{10}\)
= 4\(\frac{2}{10}\)
![]() = 4\(\frac{2}{10}\) – 2\(\frac{3}{5}\)
= 4\(\frac{2}{10}\) – 2\(\frac{3}{5}\)
![]() = \(\frac{42}{10}\) – \(\frac{13}{5}\)
= \(\frac{42}{10}\) – \(\frac{13}{5}\)
![]() = \(\frac{16}{10}\)
= \(\frac{16}{10}\)
2\(\frac{3}{5}\) + \(\frac{16}{10}\) = 4\(\frac{2}{10}\)
Question 2.
Calvin and his family went on another walk. This time, they went to the park, and then to the ice cream parlor. They stopped at the new fountain on their way home. In all, they walked 4\(\frac{3}{8}\) kilometers. How far was it from the fountain to their home? Use the map to help solve the problem. Show all your work.
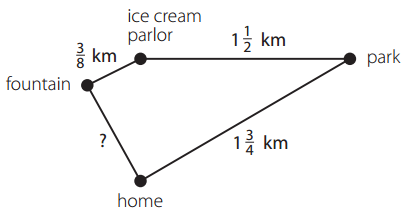
Answer:
Calvin and his family went on another walk.
Distance from home to park = 1\(\frac{3}{4}\)
Distance from park to ice cream parlor = 1\(\frac{1}{2}\)
Distance from ice cream parlor to fountain = \(\frac{3}{8}\)
Distance from fountain to home = ?
The map shape is in trapezium.
Therefore, perimeter of the trapezium = sum of all sides
perimeter = Distance from home to park + Distance from park to ice cream parlor + Distance from ice cream parlor to fountain + Distance from fountain to home
Given total distance walked = 4\(\frac{3}{8}\)
Therefore, 4\(\frac{3}{8}\) = 1\(\frac{3}{4}\) + 1\(\frac{1}{2}\) + \(\frac{3}{8}\) + ?
Distance from fountain to home = 4\(\frac{3}{8}\) – \(\frac{29}{8}\)
Distance from fountain to home = \(\frac{6}{8}\)
Distance from fountain to home = \(\frac{3}{4}\)
Bridges in Mathematics Grade 5 Student Book Unit 5 Module 2 Session 4 Answer Key
Brian’s Boxes & Kevin’s Pictures
Question 1.
Brian is filling in puzzle boxes like those below. He’s done the first one already. Look at how he filled it in, then complete the others.
ex:
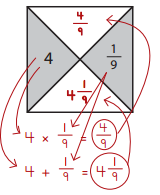
a.
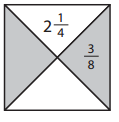
Answer: 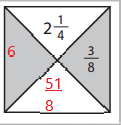
y x \(\frac{3}{8}\) = 2\(\frac{1}{4}\)
y x \(\frac{3}{8}\) = \(\frac{9}{4}\)
y = \(\frac{9}{4}\) ÷ \(\frac{3}{8}\)
y = \(\frac{9}{4}\) x \(\frac{8}{3}\)
y = 6
6 + \(\frac{3}{8}\) = \(\frac{51}{8}\)
b.
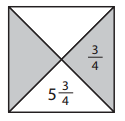
Answer: 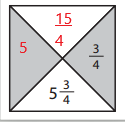
y + \(\frac{3}{4}\) = 5\(\frac{3}{4}\)
y = 5\(\frac{3}{4}\) – \(\frac{3}{4}\)
y = 5
5 x \(\frac{3}{4}\) = \(\frac{15}{4}\)
Question 2.
Make up a box challenge for Brian to solve. Fill in the entire first box to show the completed box. Then, fill in just two parts of the second box so it is ready for Brian to solve. Think carefully about which parts of the box you will leave blank.
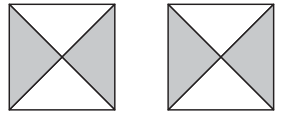
Answer:
Question 3.
Kevin has 140 pictures. He wants to sell them for $4.50 each. If Kevin sells all of his pictures, how much money will be he make? Think about the fastest way to solve this problem. Show your work.
Answer:
Number of pictures kevin has = 140
Cost of each picture he wants to sell = $4.50
total cost = 140 x 4.5 = 630
Therefore, after selling all his pictures Kevin has $630.
Question 4.
Kevin has sold pictures twice before. He made $172.95 at his first sale and $398.26 at his second sale. Show your work for the following problems.
a. How much did Kevin make from his first two sales?
Answer: $571.22
Kevin made $172.95 at his first sale.
Kevin made $398.26 at his second sale.
Kevin make from his first two sales = $172.95 + $398.26 = $571.22
b. How much more did Kevin make at his second sale than his first sale?
Answer: $225.31
Kevin made $172.95 at his first sale.
Kevin made $398.26 at his second sale.
Kevin make at his second sale than his first sale = $398.26 – $172.95 = $225.31
Bridges in Mathematics Grade 5 Student Book Unit 5 Module 2 Session 5 Answer Key
Question 1.
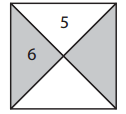
Complete the puzzle boxes.
ex:
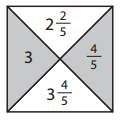
a.
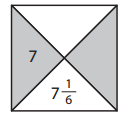
Answer: 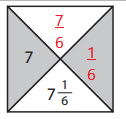
7 + y = 7\(\frac{1}{6}\)
y = 7\(\frac{1}{6}\) – 7
y = \(\frac{43}{6}\) – 7
y = \(\frac{1}{6}\)
b.
Answer: 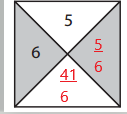
6 x y = 5
y = \(\frac{5}{6}\)
Question 2.
Fill in the blanks.
a. 13 × \(\frac{7}{7}\) = ![]()
Answer: 13
13 x \(\frac{7}{7}\) = ![]()
13 x 1 = ![]()
13 = ![]()
b. \(\frac{4}{4}\) × ![]() = 12
= 12
Answer: 12
\(\frac{4}{4}\) × ![]() = 12
= 12
1 × ![]() = 12
= 12
![]() = 12
= 12
c. 5 × \(\frac{2}{3}\) = ![]()
Answer: \(\frac{17}{3}\)
5 × \(\frac{2}{3}\) = ![]()
\(\frac{17}{3}\) = ![]()
Question 3.
Thanh ate \(\frac{7}{12}\) of his candy bar on Monday and another \(\frac{1}{3}\) of his candy bar on Tuesday. What fraction of the candy bar does Thanh have left? Show your work.
Answer: \(\frac{1}{12}\)
Let the total candy = 1
Thanh ate \(\frac{7}{12}\) of his candy bar on Monday and another \(\frac{1}{3}\) of his candy bar on Tuesday.
The amount of candy bar Thanh have left = 1 – (\(\frac{7}{12}\) + \(\frac{1}{3}\))
= 1 – \(\frac{11}{12}\)
= \(\frac{1}{12}\)
Question 4.
Charlotte and Riley walked \(\frac{6}{10}\) of a mile to school one day, and then after school they walked 8 of a mile to the store. From the store back home was another \(\frac{2}{5}\) of a mile. How far did the girls walk in all? Show your work.
Answer: 9 miles
Charlotte and Riley walked \(\frac{6}{10}\) of a mile to school one day.
And from school they walked 8 of a mile to the store.
From the store back home was another \(\frac{2}{5}\) of a mile.
Total walk the girls walked = \(\frac{6}{10}\) + 8 + \(\frac{2}{5}\)
= \(\frac{90}{10}\)
= 9 miles