Bridges in Mathematics Grade 5 Student Book Unit 5 Module 1 Answer Key

Students looking for the Bridges in Mathematics Grade 5 Student Book Answer Key Unit 5 Module 1 can find a better approach to solve the problems.

Bridges in Mathematics Grade 5 Student Book Answer Key Unit 5 Module 1

Bridges in Mathematics Grade 5 Student Book Unit 5 Module 1 Session 1 Answer Key

Mike’s Measurements

Mike is moving to a new house. He is measuring his furniture to see which items will fit in his new room. Help Mike determine the measurements of his furniture.

Question 1.
Mike’s bed has a base of 192 cm by 96 cm. What is the perimeter of the base of Mike’s bed in meters? Show your work.
Answer: 576 cm
Mike’s bed has a base of 192 cm by 96 cm.
perimeter of the base of Mike’s bed = ?
perimeter = 2 x (192 + 96)  =  2 x 288 = 576

Question 2.
Mike’s wooden storage box is 25 inches by 36 inches by 39 inches. What is the volume of Mike’s box? Show your work.
Answer:  35100 in³
Mike’s wooden storage box is 25 inches by 36 inches by 39 inches.
volume = 25 * 36 * 39 = 35100 in³

Question 3.
Mike’s room is rectangular. One wall of Mike’s new room is 3.96 meters long.
a. How long is this wall in centimeters?
Answer:  396 centimeters
1 meter = 100 centimeters
3.96 meters = ?
Therefore, 3.96 meters = 3.96 * 100 = 396 centimeters

b. How long is this wall in millimeters?
Answer: 3690 millimeters
1 meter = 1000 millimeters
3.96 meters = ?
Therefore, 3.96 * 1000 = 3960 millimeters

Question 4.
Another wall in Mike’s room is 2.51 meters long.
a. How long is this wall in centimeters?
Answer: 251 centimeters
1 meter = 100 centimeters
2.51 meters = ?
Therefore, 2.51 * 100 = 251 centimeters

b. How long is this wall in millimeters?
Answer: 2510 millimeters
1 meter = 1000 millimeters
2.51 meters  = ?
Therefore, 2.51 meters =2.51 * 1000 = 2510

Question 5.
What is the area of Mike’s room in square centimeters? Show your work.
Answer: 99369 cm²
Area of rectangle = l * b
l = 396 centimeters
b = 251 centimeters
Area = 396 * 251 =  99369 cm²

Bridges in Mathematics Grade 5 Student Book Unit 5 Module 1 Session 2 Answer Key

Work Place Instructions 5A Target One Fractions

Each pair of partners needs:

• 2 Target One Fractions Record Sheets
• 1 deck of Number Cards, with the 0s, 7s, 9s, and wild cards removed
• math journals

1. Players shuffle the deck of cards and decide who will be the dealer. The dealer gives 5 cards to each player.

2. Player 1 chooses three cards to make a whole number and a fraction that will result in a product that is as close to 1 as possible. Each card is only used once.
For the fraction, one card is the numerator and the other is the denominator. For example, if the cards 2, 5, and 8 are used, players could choose 5 × \(\frac{2}{8}\), 5 × \(\frac{8}{2}\), 2 × \(\frac{5}{8}\), etc.

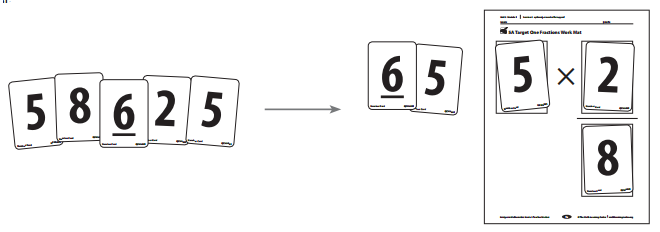
Player 1 0K, I got two 5s, a 2, a 6, and an 8. Hmm… I think I’m going to use one of the 5s as my whole number, and the 2 and the 8 for the fraction, like this.

3. Player 1 multiplies the two numbers and shows her work in her math journal. Then players discuss how to multiply the two numbers.
Player 1 I think that 5 × \(\frac{2}{8}\) is \(\frac{10}{8}\) which is 1\(\frac{2}{8}\), and that’s the same as 1\(\frac{1}{4}\).
Player 2 I thought of it as 5 × \(\frac{2}{8}\) = 5 × \(\frac{1}{4}\), so it’s \(\frac{5}{4}\). That’s also 1\(\frac{1}{4}\).

4. Player 1 writes an equation to represent her work on her record sheet.

5. Player 1 figures her score by finding the difference between the product and 1. Both Player 1 and Player 2 both record Player 1’s score on their record sheets.
A product of 1\(\frac{1}{4}\) has a score of \(\frac{1}{4}\).
A product of \(\frac{7}{8}\) has a score of \(\frac{1}{8}\).
A product of 1 has a score of 0.
At the end of each turn, players keep the 2 cards they did not use. The dealer passes out 3 new cards to each player, so each player has a total of 5 cards to begin the next round.

6. Player 2 takes a turn. Players continue to take turns until they have played 5 rounds of the game.
7. Players add the scores of all 5 rounds. The lower total score wins.

Game Variations
A. Include the wild cards in the deck. A wild card can be any numeral 1-6. Players put a star above the number made from a wild card in the equation on their record sheets.

B. Products below 1 get a positive score. Products above 1 get a negative score. Players add those scores together and the final score closest to 0 wins.
For example, a product of \(\frac{7}{8}\) would be scored as +\(\frac{1}{8}\), and a product of 1\(\frac{1}{4}\) would be scored as –\(\frac{1}{4}\).

C. Players play Target Two Fractions, trying to get as close as possible to 2 instead of 1.

Target One Fractions

In Target One Fractions, players choose 3 numbers to create a whole number and a fraction that have a product close to 1. Their score is the difference between their product and 1.

Question 1.
Claudia is playing Target One Fractions. She has these cards: 2, 3, 5, 5, 8. Help Claudia by choosing 3 cards and writing an equation she will solve.
Answer: The numbers that will yield a result closest to 1 are 2, 3 and 5 used in one of the following equations:
2 x \(\frac{3}{5}\)  = \(\frac{6}{5}\)  or 3 x \(\frac{2}{5}\)  = \(\frac{6}{5}\)

Question 2.
Ernesto is playing Target One Fractions. He chose these cards: 2, 3, 8. He made the problem 8 × \(\frac{2}{3}\).
a What is 8 × \(\frac{2}{3}\) your work.
Answer: \(\frac{16}{3}\)
8 x \(\frac{2}{3}\)  = \(\frac{16}{3}\)

b. What is Ernesto’s score?
Answer: 4 \(\frac{1}{3}\)
Ernestos’s Score is 4 \(\frac{1}{3}\)

c. How else could you arrange the numbers?
Answer: The arrangement that will yield a product closest to 1 is 2 x \(\frac{3}{8}\)

d. What would your product be? Show your work.
Answer: The cards which I have chosen are 5, 8, 6, 2, 5. I haver chosen 5, 2, 8 as my three cards.

e. What is your score?
Answer:
5 × \(\frac{2}{8}\) = 5 × \(\frac{1}{4}\), so it’s \(\frac{5}{4}\). That’s also 1\(\frac{1}{4}\).

f. What is the difference between your score and Ernesto’s? Show your work.
Answer:
Ernestos’s Score is 4 \(\frac{1}{3}\)
My score is 1\(\frac{1}{4}\)
Difference between my score and Ernesto’s is 4 \(\frac{1}{3}\) – 1\(\frac{1}{4}\)
=  \(\frac{13}{3}\) – \(\frac{5}{4}\)
= \(\frac{52 – 15}{12}\)
= \(\frac{37}{12}\)
=3 \(\frac{1}{12}\)

Bridges in Mathematics Grade 5 Student Book Unit 5 Module 1 Session 3 Answer Key

A Fraction of a Whole

Use numbers and labeled sketches to solve the problems on this page. Show your work.

Question 1.
Nathan participated in a 5K (5 kilometer) race. He walked \(\frac{1}{4}\) of the way, jogged \(\frac{3}{5}\) of the way, and ran \(\frac{3}{20}\) of the way.
a. How many kilometers did Nathan walk?
Answer: \(\frac{5}{4}\) K = 1.25 K
Total kilometers Nathan walked = 5
He walked \(\frac{1}{4}\) of the way
Therefore, number of kilometers he walked = 5 x \(\frac{1}{4}\) = \(\frac{5}{4}\) = 1.25 K

b. How many meters did Nathan walk?
Answer: 1250 meters
1 kilometer = 1000 meters
1.25 kilometers = ?
Therefore, 1.25 x 1000 = 1250 meters

c. How many kilometers did Nathan jog?
Answer: 3 k
Total kilometers Nathan walked = 5
Total kilometers Nathan jogged  = \(\frac{3}{5}\)
Therefore, number of kilometers he jogged = 5 x \(\frac{3}{5}\) = 3 K

d. How many meters did Nathan jog?
Answer: 3000 meters
1 kilometer = 1000 meters
3 kilometers = ?
Therefore, 3 x 1000 = 3000 meters

e. How far in kilometers did Nathan run?
Answer: \(\frac{3}{4}\)K = 0.75 K
Total kilometers Nathan walked = 5
Total kilometers Nathan run  = \(\frac{3}{20}\)
Therefore, number of kilometers he run = 5 x \(\frac{3}{20}\) = \(\frac{3}{4}\)K = 0.75 K

f. How many meters did Nathan run?
Answer: 750 meters
1 kilometer = 1000 meters
0.75 kilometers = ?
Therefore, 0.75 x 1000 = 750 meters

Question 2.
Deja’s bedroom is 9 square meters. She just got a new rug that covers \(\frac{3}{5}\) of her bedroom floor. How big is Deja’s new rug?
Answer:
Deja’s bedroom is 9 square meters.
She just got a new rug that covers \(\frac{3}{5}\) of her bedroom floor.
9 – \(\frac{3}{5}\)
Therefore, Deja’s new rug is

Question 3.
Write a story problem for \(\frac{2}{3}\) × 4. Then solve your own problem.
Answer: Vijay is having 4 apples. He wants to sell each apple at $ \(\frac{2}{3}\) . Find the cost of total apples after seeling?
Solution: total apples = 4
cost of each apple = \(\frac{2}{3}\)
total cost = \(\frac{2}{3}\)  x 4  = \(\frac{8}{3}\)

Question 4.
Solve the following combinations. Show your work for each.
Hint: Use one or more of the strategies on the chart you made with your classmates.
3 × \(\frac{3}{4}\) = ______________
6 × \(\frac{2}{5}\) = ______________
8 × \(\frac{2}{3}\) = ______________
Answer:
3 × \(\frac{3}{4}\) = \(\frac{9}{4}\)
6 × \(\frac{2}{5}\) = \(\frac{12}{5}\)
8 × \(\frac{2}{3}\) = \(\frac{16}{3}\)

Question 5.
Fill in the blanks.
\(\frac{1}{4}\) × ______________ = 9
\(\frac{2}{4}\) × ______________ = 9
\(\frac{3}{4}\) × ______________ = 9
\(\frac{4}{4}\) × ______________ = 9
Find and describe at least one pattern in the 4 combinations above.
Answer:
\(\frac{1}{4}\) × 36 = 9
\(\frac{2}{4}\) × 17 = 9
\(\frac{3}{4}\) × 12 = 9
\(\frac{4}{4}\) × 1= 9

Question 6.
Fill in the blanks.
\(\frac{1}{5}\) × ______________ = 15
\(\frac{1}{5}\) × ______________ = 30
\(\frac{1}{5}\) × ______________ = 60
\(\frac{1}{5}\) × ______________ = 120
Find and describe at least one pattern in the 4 combinations above.
Answer:
\(\frac{1}{5}\) × 75 = 15
\(\frac{1}{5}\) × 150 = 30
\(\frac{1}{5}\) × 300 = 60
\(\frac{1}{5}\) × 600 = 120

Question 7.
CHALLENGE Fill in the blanks.
\(\frac{5}{4}\) × ______________ = 10
\(\frac{8}{4}\) × ______________ = 9
\(\frac{3}{5}\) × ______________ = 30
\(\frac{4}{5}\) × ______________ = 60
Answer:
\(\frac{5}{4}\) × 8 = 10
\(\frac{8}{4}\) × 4.5 = 9
\(\frac{3}{5}\) × 50 = 30
\(\frac{4}{5}\) × 75 = 60

Fractions of Wholes

Question 1.
Find the product.
a. \(\frac{1}{4}\) of 7 = _____________
Answer:  \(\frac{7}{4}\)
\(\frac{1}{4}\) of 7 = \(\frac{1}{4}\) x 7
\(\frac{1}{4}\) of 7 = \(\frac{7}{4}\)

b. \(\frac{1}{5}\) × 25 = _____________
Answer: 5
\(\frac{1}{5}\) × 25 = 5

c. \(\frac{1}{3}\) of 36 = ____________
Answer: 12
\(\frac{1}{3}\) of 36 = \(\frac{1}{3}\) x 36
\(\frac{1}{3}\) of 36 = 12

d. \(\frac{3}{4}\) of 7 = _______________
Answer: \(\frac{21}{4}\)
\(\frac{3}{4}\) of 7 = \(\frac{3}{4}\) x 7
\(\frac{3}{4}\) of 7 = \(\frac{21}{4}\)

e. \(\frac{4}{5}\) × 25 = _______________
Answer: 20
\(\frac{4}{5}\) × 25 = 4 x 5
\(\frac{4}{5}\) × 25 = 20

f. \(\frac{2}{3}\) × 36 = _______________
Answer: 24
\(\frac{2}{3}\) × 36 = 2 x 12
\(\frac{2}{3}\) × 36 = 24

Question 2.
True or False?
a. \(\frac{1}{2}\) × 11 = 8 \(\frac{1}{4}\)
True
False
Answer: False
\(\frac{1}{2}\) × 11 = \(\frac{11}{2}\)  = 5.5
8 \(\frac{1}{4}\) =  \(\frac{33}{4}\) = 8.25
Therefore both are not equal

b. \(\frac{3}{5}\) of 20 = 15
True
False
Answer: False
\(\frac{3}{5}\) of 20 = \(\frac{3}{5}\) x 20 =  3 x 4 = 12
12 is not equal to 15.
therefore, both are not equal

c. \(\frac{2}{5}\) of 30 = 18
True
False
Answer: False
\(\frac{2}{5}\) of 30 = \(\frac{2}{5}\) x 30 = 12
12 is not equal to 18
Therefore, both are not equal

d. 16 × \(\frac{1}{5}\) = \(\frac{16}{5}\)
True
False
Answer: True
16 × \(\frac{1}{5}\) = \(\frac{16}{5}\)
both are equal

e. \(\frac{2}{6}\) × 21 = 7
True
False
Answer: True
\(\frac{2}{6}\) × 21 = \(\frac{1}{3}\) × 21 = 7
Therefore, both are equal

f. 24 × \(\frac{2}{3}\) = \(\frac{48}{3}\)
True
False
Answer: True
24 × \(\frac{2}{3}\) = 8 x 2 = 16
\(\frac{48}{3}\) = 16
Therefore, both are equal

Question 3.
Madeline read \(\frac{2}{3}\) of her favorite book on the car ride to her grandparents’ house. If the book had 225 pages, how many pages of the book has she read?
Answer: 150
Total number of pages in the book = 225
Madeline read \(\frac{2}{3}\) of the book
Therefore, total number of pages she read =  225  x \(\frac{2}{3}\)
= 75 x 2 = 150

Question 4.
Theo entered a race that required him to ride his bike 54 kilometers and run \(\frac{1}{6}\) as far as he bikes.
a. How many kilometers will Theo run?
Answer:  9 kilometers
Bike rides 54 kilometers
Theo runs \(\frac{1}{6}\) as far as he bikes
Therefore, number of kilometers will Theo run  = 54 x \(\frac{1}{6}\)
= 9 kilometers

b. How many meters will he run?
Answer: 9000 meters
1 kilometer = 1000 meters
9 kilometers = ?
Therefore, 9 x 1000 = 9000 meters

Bridges in Mathematics Grade 5 Student Book Unit 5 Module 1 Session 4 Answer Key

Thinking About Strategy

Question 1.
Anna is playing Target One Fractions. She has these cards: 4, 3, 6, 4, 2.
a. What three cards should she choose to make a whole number and fraction whose product is close to 1?
Answer: The 3 numbers that will result in the product closest to 1 are 2, 3 and 6 used in one of the two equations are 2 x \(\frac{3}{6}\)  or 3 x \(\frac{2}{6}\)

b. Write an equation for the problem Anna will solve.
Answer:
Anna’s problem equation would be the following two:
2 x \(\frac{3}{6}\)  or 3 x \(\frac{2}{6}\)

c. Solve the problem.
Answer:
There are two possibilities.
1) 2 x \(\frac{3}{6}\) =  \(\frac{6}{6}\) = 1
2) 3 x \(\frac{2}{6}\) =  \(\frac{6}{6}\) = 1

d. What is Anna’s score for this round?
Answer: 1
Whatever equation she would choose, her score would be 1

Question 2.
Multiply.
Hint: Use one of the strategies on the class poster from today’s session.
\(\frac{3}{5}\) × 4 = _______________
\(\frac{4}{5}\) × 3 = _______________
\(\frac{4}{5}\) × 16 = _______________
Answer:
\(\frac{3}{5}\) × 4 = \(\frac{12}{5}\) 
\(\frac{4}{5}\) × 3 = \(\frac{12}{5}\)
\(\frac{4}{5}\) × 16 = \(\frac{64}{5}\)

Question 3.
CHALLENGE Morgan thought she would be able to sell 75 plants for the school fundraiser. So far, she has sold \(\frac{2}{3}\) of her goal. Morgan’s friend Billy has sold \(\frac{4}{5}\) of his goal of 60 plants.
a. Make a prediction: which of the two students has sold more plants?
Answer:  Morgan sold more plants than Billy
Morgan goal = 75 plants
Total plants Morgan sold = \(\frac{2}{3}\) of her goal
= \(\frac{2}{3}\) x 75
= 2 x 25
= 50
Therefore, Morgan sold 50 plants.
Billy goal = 60 plants
Total plants Billy sold = \(\frac{4}{5}\) of his goal of 60 plants.
= \(\frac{4}{5}\) x 60
= 4 x 12
= 48
Therefore, Billy sold 48 plants
So, Morgan sold more plants than Billy

b. How many plants has each student sold? Show your work.
Answer:  Morgan sold 50 plants and Billy sold 48 plants.
Morgan goal = 75 plants
Total plants Morgan sold = \(\frac{2}{3}\) of her goal
= \(\frac{2}{3}\) x 75
= 2 x 25
= 50
Therefore, Morgan sold 50 plants.
Billy goal = 60 plants
Total plants Billy sold = \(\frac{4}{5}\) of his goal of 60 plants.
= \(\frac{4}{5}\) x 60
= 4 x 12
= 48
Therefore, Billy sold 48 plants

Bridges in Mathematics Grade 5 Student Book Unit 5 Module 1 Session 5 Answer Key

Ryan’s Baseball Cards

Question 1.
Ryan has 48 baseball cards. He gives some of them away to his friends. Help Ryan figure out how many cards each of his friends will get. Show your work.
a. If Ryan gives \(\frac{1}{4}\) of his 48 cards to Anna, how many cards does he give Anna?
Answer: 12 cards
Total cards = 48 cards
Ryan gives \(\frac{1}{4}\) of his 48 cards to Anna
Therefore, number of cards he gives to Anna =\(\frac{1}{4}\) x 48
= 12
So, Ryan gives 12 cards to Anna

b. If Ryan gives \(\frac{3}{8}\) of his 48 cards to Josiah, how many cards does he give Josiah?
Answer: 18 cards
Total cards = 48 cards
Ryan gives \(\frac{3}{8}\) of his 48 cards to Josiah
Therefore, number of cards he gives to Josaih =\(\frac{3}{8}\) x 48
= 18
So, Ryan gives 18 cards to Josaih

c. If Ryan gives \(\frac{2}{6}\) of his 48 cards to Max, how many cards does he give Max?
Answer: 16 cards
Total cards = 48 cards
Ryan gives \(\frac{2}{6}\) of his 48 cards to Max
Therefore, number of cards he gives to Anna =\(\frac{2}{6}\) x 48
= 16
So, Ryan gives 16 cards to Max.

d. How many cards does Ryan have left? What fraction of his original 48 cards is this?
Answer: 2 cards
Total cards = 48 cards
Therefore, number of cards Ryan have  = total cards – (Anna cards + Josiah cards + Max cards)
= 48 – (12 + 18 +16)
= 2
So, Ryan have 2 cards

Question 2.
Solve the problems below.
\(\frac{2}{3}\) + \(\frac{5}{6}\) = ________________
1\(\frac{1}{3}\) – \(\frac{7}{8}\) = ________________
1\(\frac{4}{5}\) + 1\(\frac{3}{10}\) = _______________
16 × \(\frac{7}{8}\) = _______________
\(\frac{4}{5}\) × 24 = _______________
27 × \(\frac{4}{9}\) = _______________
16\(\frac{1}{8}\) – 15\(\frac{3}{5}\) = _______________
208\(\frac{4}{7}\) + 201\(\frac{3}{4}\) = ________________
20\(\frac{1}{6}\) – 15\(\frac{3}{5}\) = ______________
Answer:
\(\frac{2}{3}\) + \(\frac{5}{6}\) = \(\frac{4}{6}\) + \(\frac{5}{6}\)  = \(\frac{9}{6}\) = \(\frac{3}{2}\)
1\(\frac{1}{3}\) – \(\frac{7}{8}\) = \(\frac{4}{3}\) – \(\frac{7}{8}\) = \(\frac{32}{24}\) – \(\frac{21}{24}\) = \(\frac{11}{24}\)
1\(\frac{4}{5}\) + 1\(\frac{3}{10}\) = \(\frac{9}{5}\) + \(\frac{13}{10}\) = \(\frac{18}{10}\) + \(\frac{13}{10}\)  = \(\frac{31}{10}\)
16 × \(\frac{7}{8}\) = 2 x 7 = 14
\(\frac{4}{5}\) × 24 =\(\frac{96}{5}\)
27 × \(\frac{4}{9}\) =  3 x 4 = 12
16\(\frac{1}{8}\) – 15\(\frac{3}{5}\) = \(\frac{129}{8}\) – \(\frac{78}{5}\) = \(\frac{645}{40}\) – \(\frac{624}{40}\) = \(\frac{21}{40}\)
208\(\frac{4}{7}\) + 201\(\frac{3}{4}\) = \(\frac{1460}{7}\) + \(\frac{807}{4}\) = \(\frac{5840}{28}\) + \(\frac{5649}{28}\) = \(\frac{11489}{40}\)
20\(\frac{1}{6}\) – 15\(\frac{3}{5}\) = \(\frac{121}{6}\) – \(\frac{78}{5}\) = \(\frac{605}{30}\) – \(\frac{468}{30}\) = \(\frac{137}{30}\)