Students looking for the Bridges in Mathematics Grade 5 Student Book Answer Key Unit 4 Module 3 can find a better approach to solve the problems.
Bridges in Mathematics Grade 5 Student Book Answer Key Unit 4 Module 3
Bridges in Mathematics Grade 5 Student Book Unit 4 Module 3 Session 1 Answer Key
Double-Digit Multiplication Sketches
Question 1.
Mrs. Hill’s preschool classroom is 16 feet wide and 28 feet long. She is planning to divide it into 4 sections. Here is her plan. Use a multiplication equation to label the area of each section (in square feet).
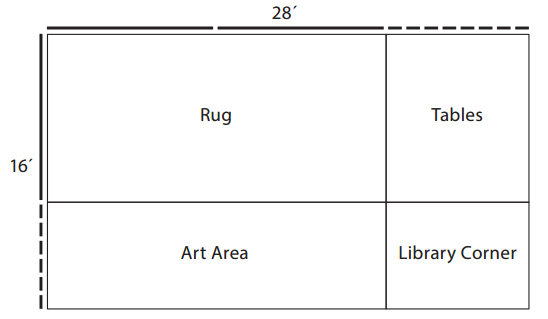
a. What is the total area of the 16-by-28-foot classroom? Show your work.
Answer:
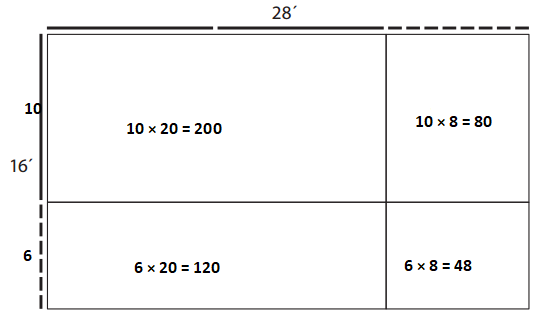
200
120
+80
+48
448
So, the total area of the 16-by-28-foot classroom is 448 sq. units.
Question 2.
Write the answers.
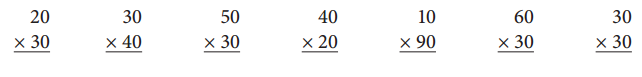
Answer:
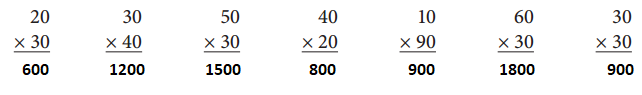
By multiplying 20 and 30 we get 600
By multiplying 30 and 40 we get 1200
By multiplying 50 and 30 we get 1500
By multiplying 10 and 90 we get 900
By multiplying 60 and 30 we get 1800
By multiplying 30 and 30 we get 900
Question 3.
Sketch an array for each of the frames below. Label each part with a multiplication equation to show its area. Then find the total area of the array.
a.
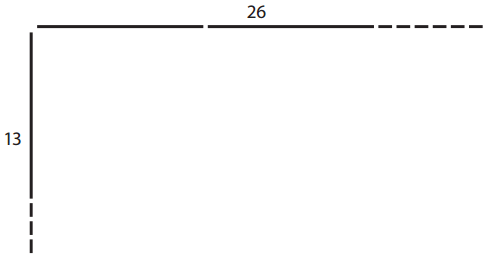
total area = _____________
Answer:
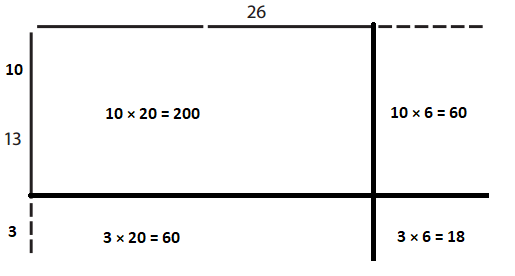
10 × 20 = 200
10 × 6 = 60
3 × 20 = 60
3 × 6 = 18
200 + 60 + 60 + 18 = 338.
So, the total area is 338 sq units.
b.
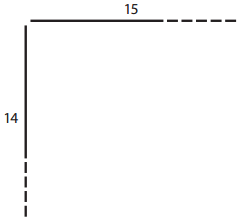
total area = _____________
Answer:
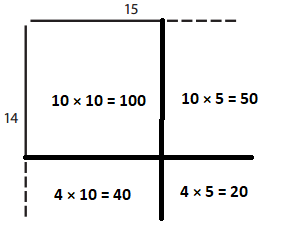
100 + 50 + 40 + 20 = 210
So, the total area is 210 sq. units.
c.

total area = _____________
Answer:
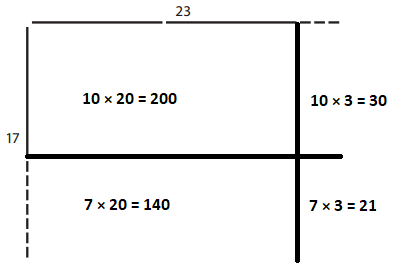
200 + 30 + 140 + 21 = 391
So, the total area is 391 sq. units
Question 4.
Write the answers.
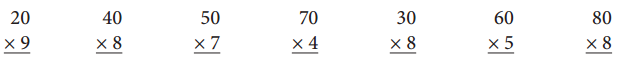
Answer:
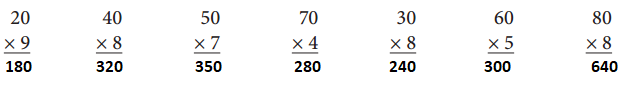
By multiplying 20 and 9 we get 180
By multiplying 40 and 8 we get 320
By multiplying 50 and 7 we get 350
By multiplying 70 and 4 we get 280
By multiplying 60 and 5 we get 300
By multiplying 80 and 8 we get 640
Work Place Instructions 4C Beat the Calculator: Multiplication
Each pair of players needs:
- 1 set of Beat the Calculator: Multiplication Cards
- scratch paper and pencils (optional)
- 1 calculator that follows order of operations
Some calculators will not work for this game. You can check a calculator by entering 1 + 3 × 2 = . If the answer shown is 7, the calculator will work for this game.
1. Shuffle the cards, lay them face-down, and decide who will use the calculator first.
2. Player 1 turns over a card so both players can see it.
3. Player 1 enters the problem exactly as it is written on the card.
Remember, \(\frac{1}{4}\) of 60 means \(\frac{1}{4}\) × 60 and can be entered on a calculator as 1 ÷ 4 × 60.
\(\frac{3}{5}\) of 50 means \(\frac{3}{5}\) × 50 and can be entered on a calculator as 3 + 5 × 50.
4. At the same time, Player 2 evaluates the expression using the most efficient strategy she can think of, either mentally or on paper.
5. The player who gets the correct answer first keeps the card.
6. Players compare answers and share strategies for evaluating the expression.
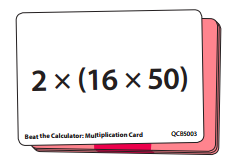
Maria If you switch the 16 and the 50 inside the parentheses and then move the parentheses, it’s (2 × 50) × 16. That’s 1,600.
Tyrell You gave the answer of 1,600 faster than I could type it into the calculator!
7. Players switch roles and draw again.
• This time, Player 2 has the calculator.
8. The player with the most cards at the end wins.
Game Variations
A. Players make up their own problems, mix them up, and then choose from those problems.
B. Instead of racing the calculator, players race each other.
C. Players play cooperatively by drawing a card and discussing their preferred mental strategy.
D. Players spread the cards face-down on the table. Each player chooses a different card at the same time
Answer:
More About Quarters
Question 1.
Fill in the blanks to complete each of the box challenge puzzles below. Remember that the number at the top is the product of the two numbers in the middle, and the number at the bottom is the sum of the two numbers in the middle.
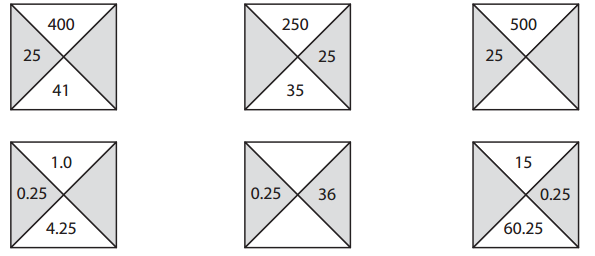
Answer:
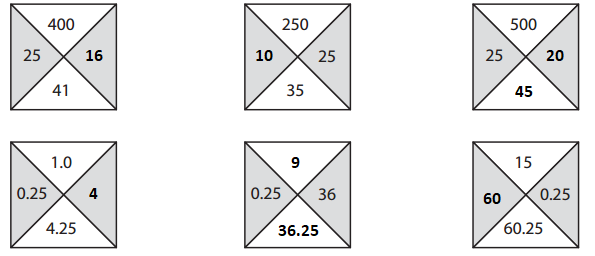
400 ÷ 25 = 16
250 ÷ 25 = 10
500 ÷ 25 = 20
25 + 20 = 45
1 ÷ 0.25 = 4
0.25 × 36 = 9
0.25 + 36 = 36.25
15 ÷ 0.25 = 60
Question 2.
Jami is completing the following box challenge and says that the missing number on the right is 100\(\frac{1}{4}\) and the missing number on the bottom is 1004. Do you agree or disagree? Explain why.
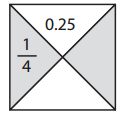
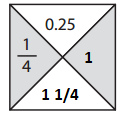
Answer:
0.25 ÷ \(\frac{1}{4}\) = 1
\(\frac{1}{4}\) × 1 = \(\frac{1}{4}\)
\(\frac{1}{4}\) + 1 = 1\(\frac{1}{4}\)
Question 3.
Find the product or quotient.
a. 30 × 25 = _____________
Answer:
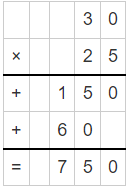
By multiplying 30 and 25 we get 750.
So, the product is 750.
b. 750 ÷ 25 = _____________
Answer:
750 ÷ 25
= 750/25 = 30
The quotient is 750 and 25 is 30.
c. 7500 ÷ 25 = ______________
Answer:
7500 ÷ 25
= 7500/25 = 300
The quotient is 7500 and 25 is 300.
d. 7550 ÷ 25 = ______________
Answer:
7550 ÷ 25
7500/25 = 302
The quotient is 7550 and 25 is 302.
Question 4.
Tell how you used one of the combinations in problem 3 to help solve another one of the combinations in that problem.
Answer: Multiplication is an operation that represents the basic idea of repeated addition of the same number. In problem 3 we used double digit multiplication strategy to find the product.
Bridges in Mathematics Grade 5 Student Book Unit 4 Module 3 Session 2 Answer Key
Double-Digit Multiplication
Question 1.
Find the product of each pair of numbers below. Make a labeled sketch to help, or just use numbers. Show all of your work.
ex:
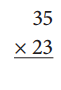
Answer: 805
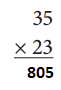
By multiplying 35 and 23 we get 805.
a.
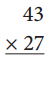
Answer: 1161
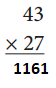
By multiplying 43 and 27 we get 1161.
b.
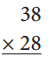
Answer: 1064
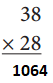
By multiplying 38 and 28 we get 1064.
c.
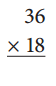
Answer: 648
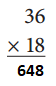
By multiplying 36 and 18 we get 648.
d.
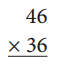
Answer: 1656
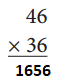
By multiplying 46 and 36 we get 1656.
Question 2.
Solve the story problems below. Make a labeled sketch to help, or just use numbers. Show all of your work.
a. Jon works at T-Shirts R Us. Yesterday, he unpacked 36 boxes of new shirts. Each box had 24 shirts in it. How many shirts did he unpack?
Answer:
Given,
Jon works at T-Shirts R Us. Yesterday, he unpacked 36 boxes of new shirts.
Each box had 24 shirts in it.
36 × 24 = 864 shirts
Thus he unpack 864 shirts.
b. Jon made 27 stacks of long-sleeved T-shirts. He put 18 shirts in each stack. How many shirts did he stack in all?
Answer:
Given,
Jon made 27 stacks of long-sleeved T-shirts.
He put 18 shirts in each stack.
27 × 18 = 486
Thus he stack 486 stacks in all.
c. CHALLENGE Then Jon made 28 stacks of short-sleeved T-shirts. He put 25 shirts in each stack. The store he works for had to pay $3.99 for each shirt. How much did they have to pay for all the shirts Jon stacked?
Answer:
Given,
Jon made 28 stacks of short-sleeved T-shirts. He put 25 shirts in each stack.
28 × 25 = 700 shirts
700 × $3.99 = $2793
Reasonable Estimates & Partial Products
Question 1.
Circle the most reasonable estimate for each multiplication problem.
a. 23 × 21
400
600
4,000
6,000
Answer:
The estimated multiplication is 20 × 20 = 400
23 × 21 = 483
400 is a reasonable estimate.
b. 31 × 19
600
700
6,000
7,000
Answer:
30 × 20 = 600
31 × 19 = 589
600 is a reasonable estimate.
c. 312 × 18
600
800
6,000
10,000
Answer:
300 × 20 = 6000
312 × 18 = 5616
6000 is a reasonable estimate.
d. 96 × 33
270
1,000
3,000
27,000
Answer:
100 × 30 = 3000
96 × 33 = 3168
3000 is a reasonable estimate.
Question 2.
Use partial products to solve each problem below. Draw lines between the digits to show which numbers you multiplied.
ex:
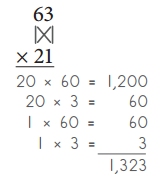
a.
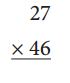
Answer: 1242
20 × 40 = 800
20 × 6 = 120
7 × 40 = 280
7 × 6 = 42
800 + 120 + 280 + 42 = 1242
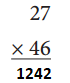
b.
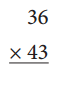
Answer: 1548
30 × 40 = 1200
30 × 3 = 90
6 × 40 = 240
6 × 3 = 18
1200 + 90 + 240 + 18 = 1548
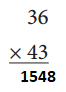
c.
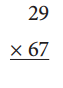
Answer: 1943
20 × 60 = 1200
20 × 7 = 140
9 × 60 = 540
9 × 7 = 63
1200 + 140 + 540 + 63 = 1943
d.
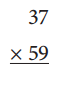
Answer: 2183
30 × 50 = 1500
30 × 9 = 270
7 × 50 = 350
7 × 9 = 63
1500 + 270 + 350 + 63 = 2183
e.
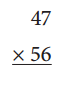
Answer: 2632
40 × 50 = 2000
40 × 6 = 240
7 × 50 = 350
7 × 6 = 42
2000 + 240 + 350 + 42 = 2632
Bridges in Mathematics Grade 5 Student Book Unit 4 Module 3 Session 3 Answer Key
Moving Toward the Standard Algorithm
How does the standard multiplication algorithm work?
- It goes from bottom to top.
- It goes from right to left.
- It starts with the 1s.
ex:
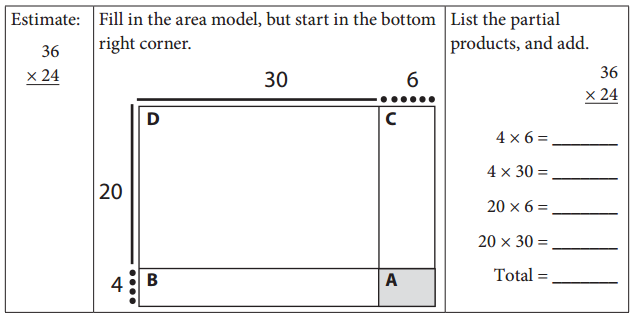
Answer:
36 × 24 = 864
4 × 6 = 24
4 × 30 = 120
20 × 6 = 120
20 × 30 = 600
24 + 120 +120 +600 = 864
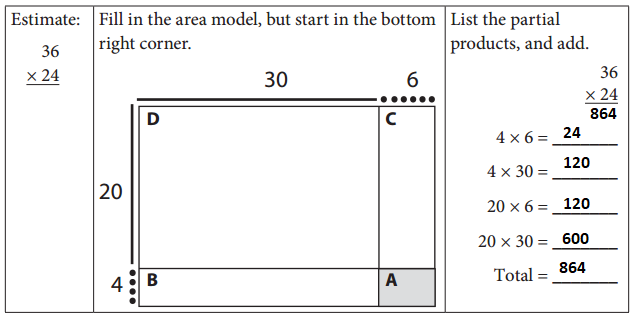
Question 1.
Practice working from bottom to top, right to left.
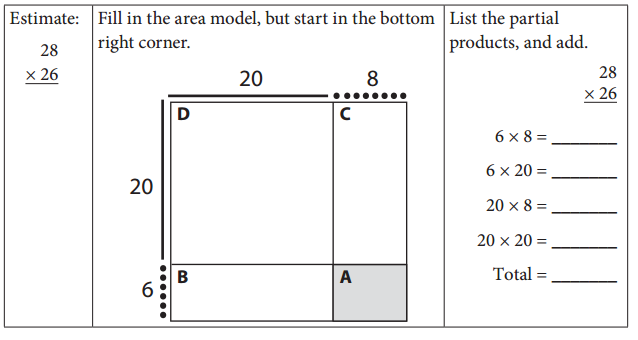
Answer:
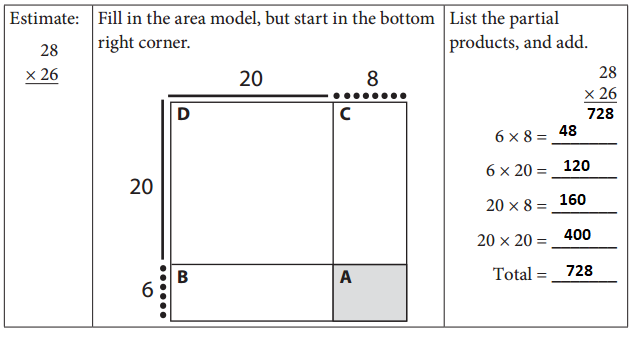
28 × 26 = 728
6 × 8 = 48
6 × 20 = 120
20 × 8 = 160
20 × 20 = 400
48 + 120 + 160 + 400 = 728
Question 2.
Practice again. This time, list the partial products in the third column. Remember to go in order from region A to region D.
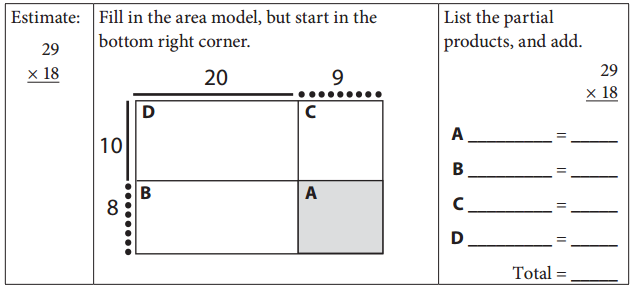
Answer:
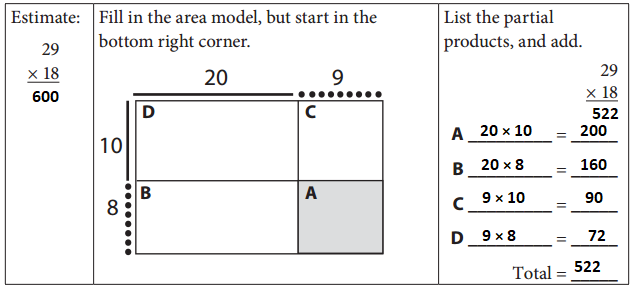
Estimate: 30 × 20 = 600
29 × 18 = 522
20 × 10 = 200
20 × 8 = 160
9 × 10 = 90
9 × 8 = 72
200 + 160 + 90 + 72 = 522
Question 3.
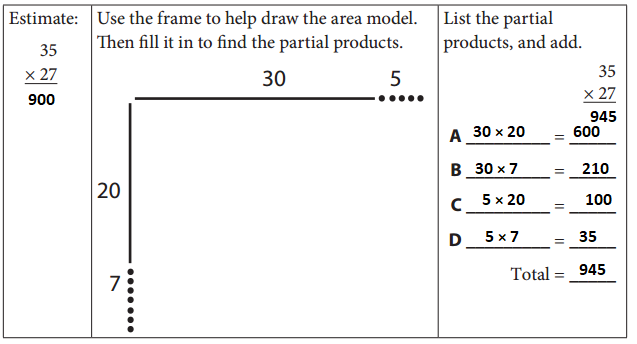
Practice again. This time, you use the frame to help draw in the area model. Then label it, list the partial products, and add. Go in order from region A to region D.
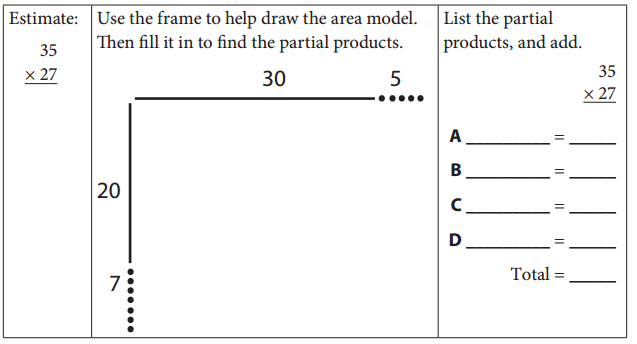
Answer:
Estimate: 30 × 30 = 900
35 × 27 = 945
30 × 20 = 600
30 × 7 = 210
5 × 20 = 100
5 × 7 = 35
600 + 210 + 100 + 35 = 945
Question 4.
Multiply.

Answer:

By multiplying 30 and 40 we get 1200.
By multiplying 40 and 50 we get 2000.
By multiplying 20 and 70 we get 1400.
By multiplying 50 and 50 we get 2500.
By multiplying 80 and 30 we get 2400.
By multiplying 60 and 70 we get 4200.
Bottom to Top, Right to Left
Question 1.
For each problem below, sketch and label a 4-part area model. Then list the partial products in order from bottom right corner to top left corner, and add them to get the total.
ex: 23 × 27
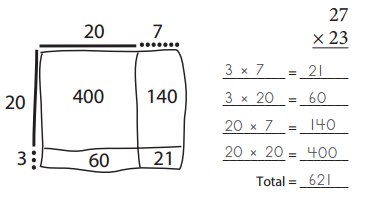
a. 24 × 35
Answer:
35 × 24 = 840
30 × 20 = 600
30 × 4 = 120
5 × 20 = 100
5 × 4 = 20
600 + 120 + 100 + 20 = 840
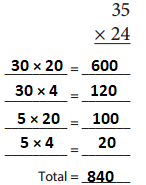
b. 26 × 43
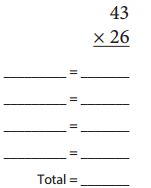
Answer:
43 × 26 = 1118
40 × 20 = 800
40 × 6 = 240
3 × 20 = 60
3 × 6 = 18
800 + 240 + 60 + 18 = 1118
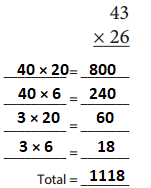
Question 2.
Practice listing and adding the partial products in the same order as you did above, without the labeled sketches.
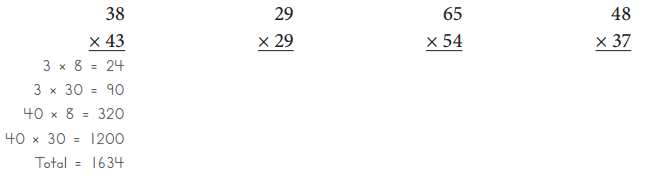
Answer:
29 × 29 = 841
65 × 54 = 3510
48 × 37 = 1776
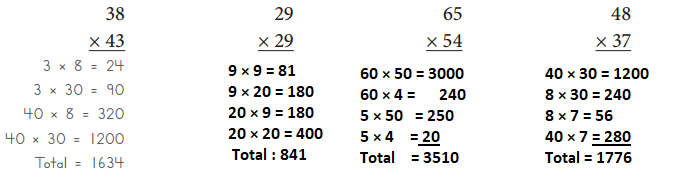
Bridges in Mathematics Grade 5 Student Book Unit 4 Module 3 Session 4 Answer Key
Understanding the Standard Algorithm
Example
Let’s use the standard algorithm first.
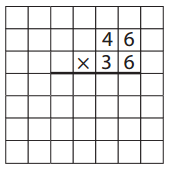
Now let’s use a labeled area model and the 4 partial products method to check our work. Remember to work from bottom to top, right to left, starting with region A.
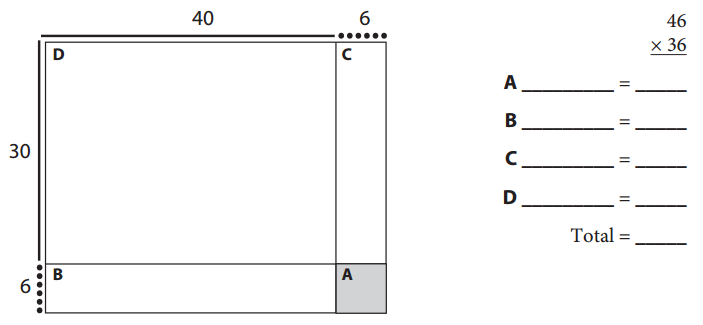
Question 1.
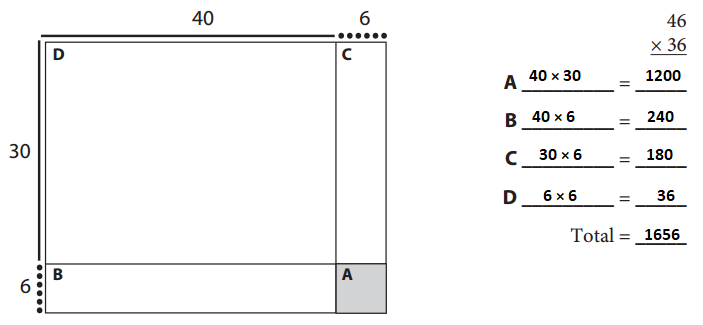
Can you find the numbers we got by using the sketch and the four partial products method in the standard algorithm? Where are they?
Answer:
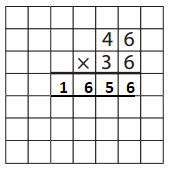
46 × 36 = 1656
40 × 30 = 1200
40 × 6 = 240
6 × 6 = 36
6 × 30 = 180
1200 + 240 + 180 + 36 = 1656
Question 2.
What are some things you need to pay attention to when you use the standard multiplication algorithm?
Answer:
The standard algorithm of multiplication is based on the principle that you already know: multiplying in parts simply multiply ones and tens separately, and add. In the standard way the adding is done at the same time as multiplying.
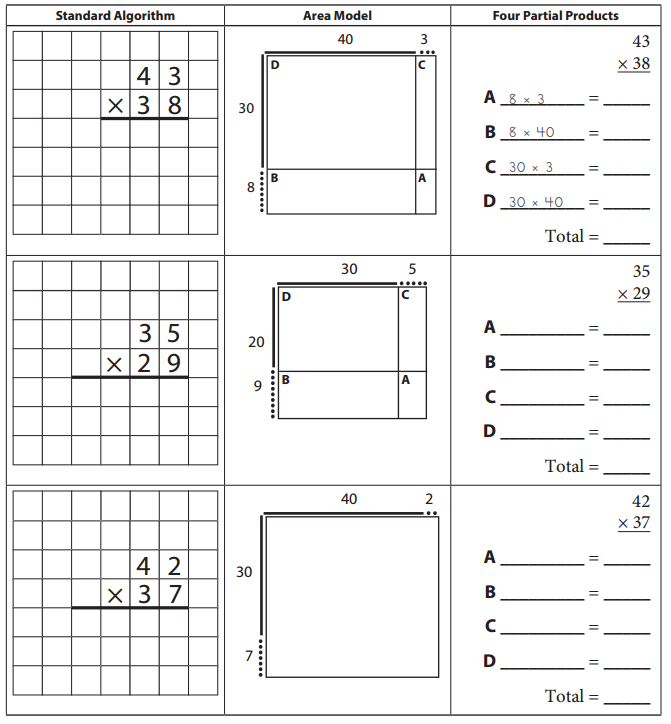
Question 3.
Practice on your own. For each problem below:
- Use the standard algorithm to get the answer.
- Then complete the area model for the problem by labeling each region.
- Finally, write out the four partial products and add them to double-check your work with the standard algorithm.
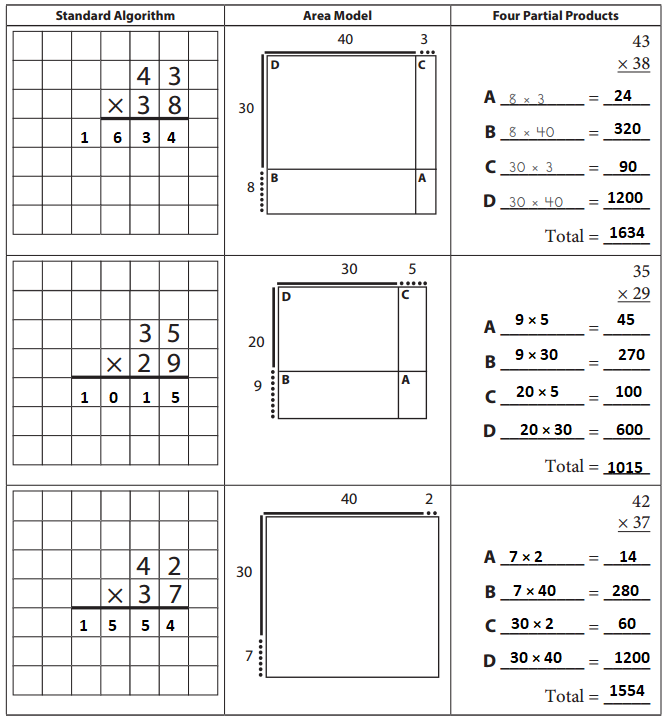
Answer:
43 × 38 = 1634
35 × 29 = 1015
42 × 37 = 1554
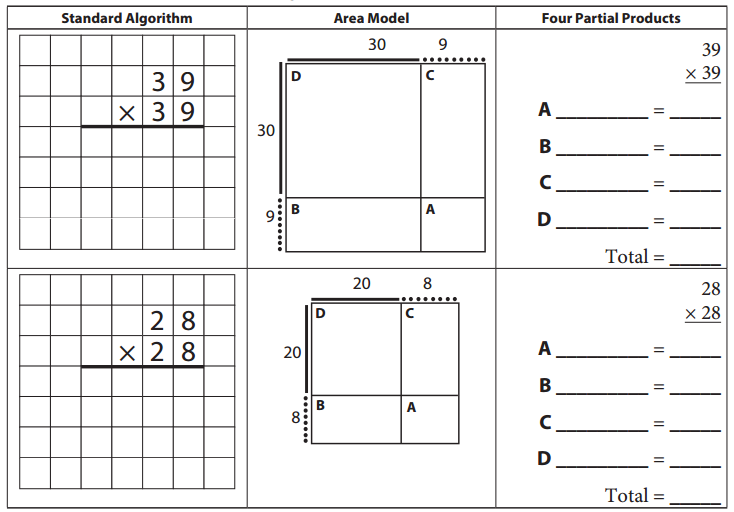
Al’s Practice Sheet
Question 1.
For each problem below:
- Use the standard algorithm to get the answer.
- Then complete the area model for the problem by labeling each region.
- Finally, write out the four partial products and add them to double-check your work with the standard algorithm.
Answer:
39 × 39 = 1521
28 × 28 = 784
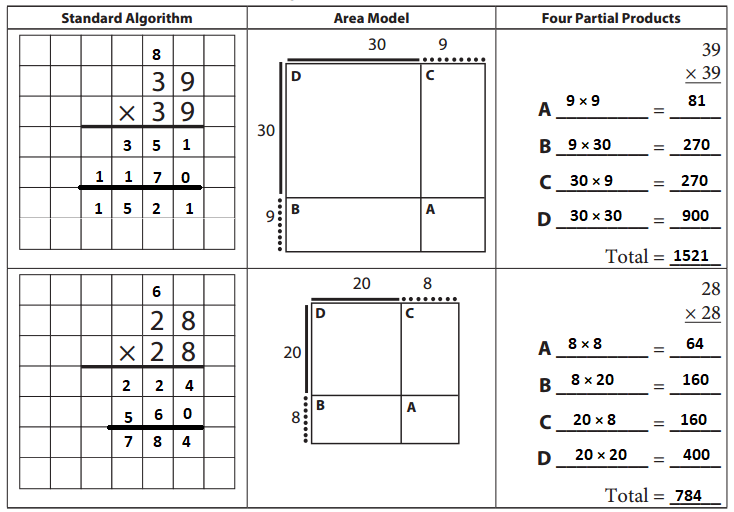
Question 2.
Al is using the standard multiplication algorithm, but he hasn’t filled in all the numbers. Help him complete each problem by filling in the gray boxes correctly.
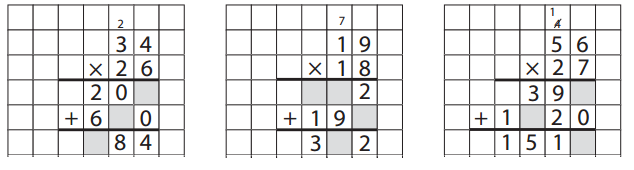
Answer:
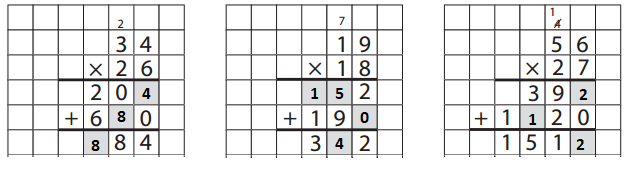
Bridges in Mathematics Grade 5 Student Book Unit 4 Module 3 Session 5 Answer Key
Fill in the Boxes
For each problem below, fill in the boxes using the standard multiplication algorithm. Then double-check your work by listing and adding the partial products.
a.
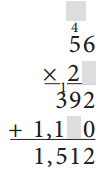
List and add the four partial products for problem a to double-check your work.
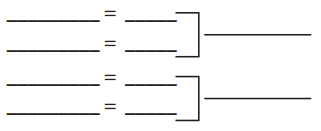
Total = _____________
Answer:
1512 ÷ 56 = 27
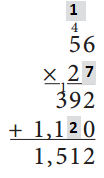
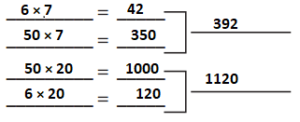
6 × 7 = 42
50 × 7 = 350
50 × 20 = 1000
6 × 20 = 120
1000 + 350 + 120 + 42 = 1512
b.
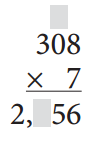
List and add the three partial products for problem b to double-check your work.
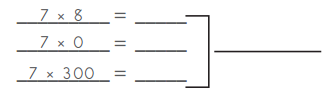
Total = _____________
Answer:
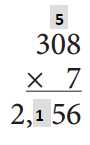
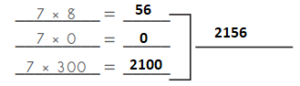
c.
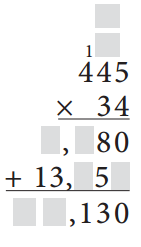
List and add all six partial products for problem c to double-check your work.
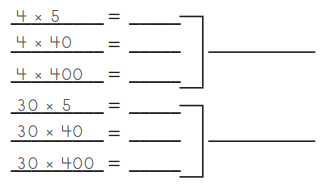
Total = _____________
Answer:
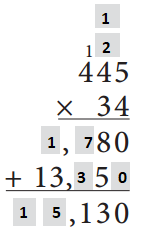
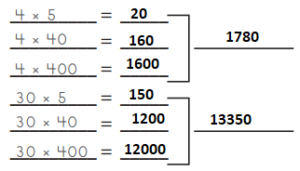
20 + 160 + 1600 + 150 + 1200 + 12000 = 15,130
Total = 15,130
Solving Problems with the Standard Algorithm
Question 1.
For each problem below:
- Use the standard algorithm to solve the problem or fill in the boxes that have been left blank.
- List and add the partial products to double-check your answer.
Note: If you want, you can use the partial product method first, and then use the standard algorithm to solve the problem again.
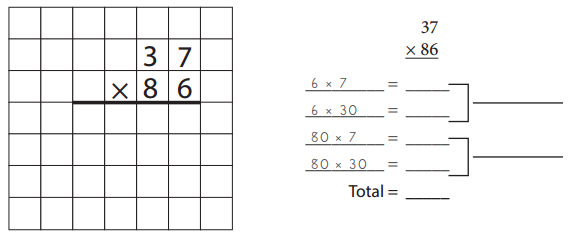
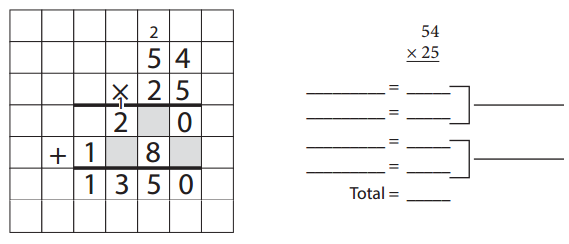
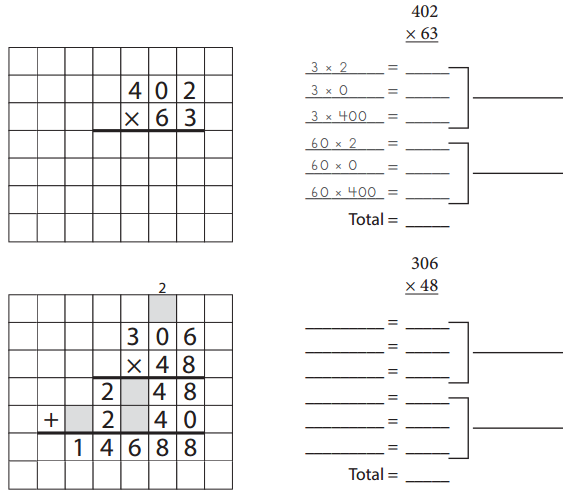
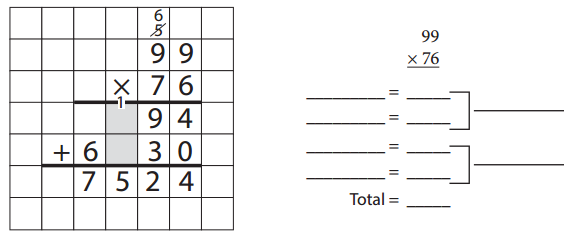
Answer:
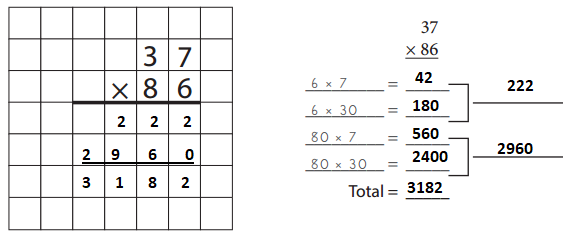
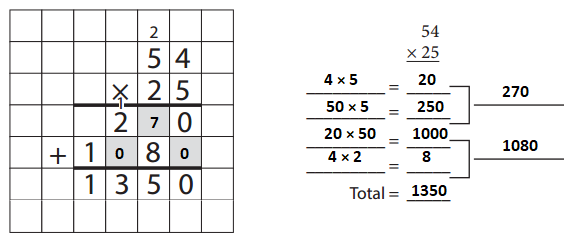
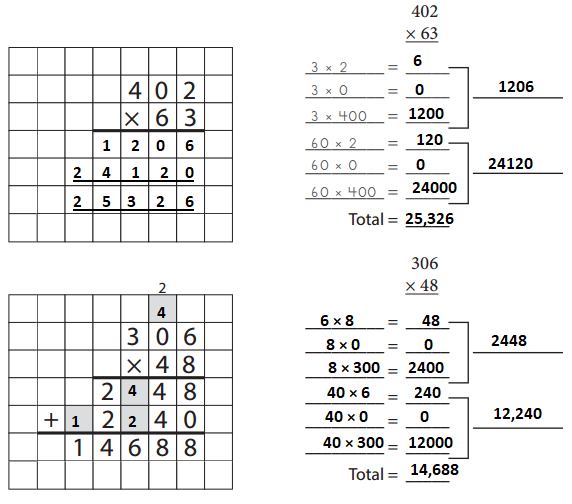
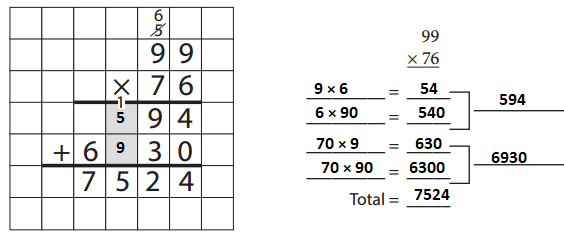
Question 2.
CHALLENGE Choose one combination from problem 1 that you could solve more efficiently with a strategy other than the standard algorithm or listing and adding the partial products. How would you solve it? Show your work on a separate sheet.
Answer:
We can use doubling and halving methods to solve the combination from problem 1.
Alex & the Algorithm
Question 1.
Alex is practicing solving problems using the standard algorithm for multiplication. He knows the first step, but then he gets stuck. Finish these problems Alex started.
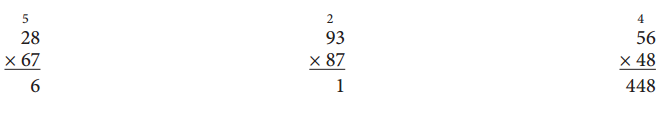
Answer:
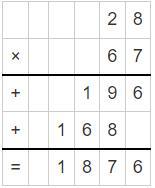
By multiplying 28 and 67 we get 1876.
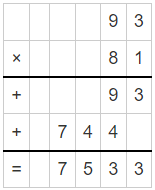
By multiplying 93 and 81 we get 7533.
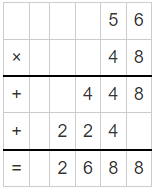
By multiplying 56 and 48 we get 2688.
Question 2.
When using the algorithm, Alex doesn’t understand why he needs to write a zero in the ones place of the second partial product.
a. Explain to Alex why he needs to do this.
Answer: In the second multiplication, one has to add a zero in one’s place. This is because we’re actually multiplying by a multiple of ten.
b. What would happen if Alex did not place a zero there?
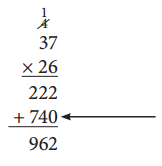
Answer:
In second-line multiplication, we are multiplying by a multiple of ten so we have to add 0 in the one’s place. If you don’t add 0 in the ones place the product will be wrong.
Question 3.
Fill in the boxes to complete the problems.
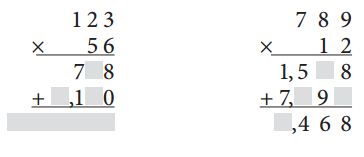
Answer:
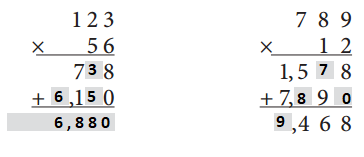
By multiplying 123 and 56 we get 6,880.
By multiplying 789 and 12 we get 9,468.
Bridges in Mathematics Grade 5 Student Book Unit 4 Module 3 Session 6 Answer Key
25 × 64
Use each of the strategies below to solve 25 × 64.
Question 1.
Area Model & Four Partial Products
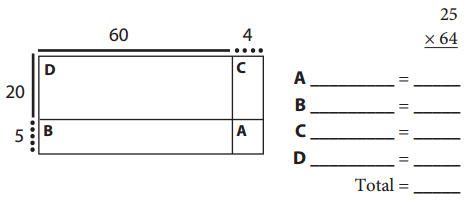
Answer:
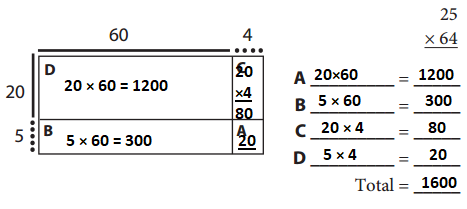
25 × 64 = 1600
By multiplying 25 and 64 we get 1600.
Question 2.
Doubling & Halving
25 × 64 = ___________ × __________ = __________ × ___________ = ____________
Answer:
To use halving and doubling, you simply half one of the factors and double the other.
25 × 64 can be written as 50 × 16
25 × 64 can be written as 12.5 × 128
25 × 64 = 50 × 16 = 12.5 × 128 = 1600
Question 3.
Ratio Table

Answer:

64 × 1 = 64
64 × 2 = 128
64 × 3 = 192
64 × 4 = 256
64 × 5 = 320
64 × 6 = 384
64 × 7 = 448
64 × 8 = 512
Question 4.
Using Quarters
a. 64 × \(\frac{1}{4}\) = ______________
Answer:
64 × \(\frac{1}{4}\) = 16
By multiplying 64 and 1/4 we get 16
b. 64 × 0.25 = _____________
Answer
0.25
×64
16
By multiplying 0.25 and 64 we get 16.
c. How can you use these results to find 25 × 64?
Answer:
64
×25
1600
Question 5.
The Standard Multiplication Algorithm
a. Solve the problem.
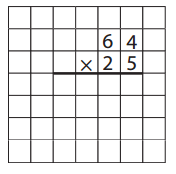
Answer:
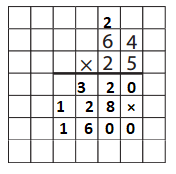
b. Which strategy do you think is best for this combination? Why?
Answer:
The Multiplication Principle states that if one task can be performed in m ways and a second task can be performed independently of the first in n ways, then there are mn ways of performing both tasks.
Bridges in Mathematics Grade 5 Student Book Unit 4 Module 3 Session 7 Answer Key
Story Problems
Solve each problem. Use the standard multiplication algorithm for two problems and any strategy you choose for the rest. Show your work. Explain your choice of strategy.
Question 1.
Connor is trying to drive his car less frequently. He started by figuring out how much he drives in a typical year. If Connor drives about 98 miles each week, how much does he drive in one year (52 weeks)?
Solve the problem:
What strategy did you use? Why?
Answer:
Given,
Connor is trying to drive his car less frequently.
He started by figuring out how much he drives in a typical year.
98 × 52 = 5096
Thus Connor drive 5096 miles in one year.
Question 2.
Taylor has a cupcake business. She packages cupcakes in cartons that hold 25 cupcakes. The Wildwood School ordered 184 cartons of Taylor’s cupcakes. How many cupcakes did the Wildwood School order?
Solve the problem:
What strategy did you use? Why?
Answer:
Given,
Taylor has a cupcake business. She packages cupcakes in cartons that hold 25 cupcakes.
The Wildwood School ordered 184 cartons of Taylor’s cupcakes.
184 × 25 = 4600 cupcakes
Thus Wildwood School order 4600 cupcakes.
Question 3.
Victoria signed up for a two-year cell phone plan. She will pay $37.50 a month for 24 months. How much will Victoria have paid at the end of her two-year plan?
Solve the problem:
What strategy did you use? Why?
Answer:
Given,
Victoria signed up for a two-year cell phone plan.
She will pay $37.50 a month for 24 months.
$37.50 × 24 = $900
Thus Victoria paid $900 at the end of her two-year plan.
Question 4.
Aaron wants to visit Australia. He found a plane ticket for $2,150. If Aaron saves $86 a week, how many weeks will it take him to save enough money to go to Australia?
Solve the problem:
What strategy did you use? Why?
Answer:
Given,
Aaron wants to visit Australia. He found a plane ticket for $2,150.
Aaron saves $86 a week
$2150 ÷ $86 = 25
Thus it takes 25 weeks for him to save enough money to go to Australia.
Question 5.
Tina’s family drinks about 128 ounces of milk in one week. How many ounces of milk do they drink in 36 weeks?
Solve the problem:
What strategy did you use? Why?
Answer:
Given,
Tina’s family drinks about 128 ounces of milk in one week.
128 × 36 = 4608 ounces.
Thus Tina’s family drinks 4608 ounces of milk in 36 weeks.
Question 6.
Max is building a cage for his ducks. The base of the cage is 208 square feet. If one side is 13 feet, how long is the other side? The cage is a rectangular prism.
Solve the problem:
What strategy did you use? Why?
Answer:
Given,
Max is building a cage for his ducks. The base of the cage is 208 square feet.
one side is 13 feet
We know that
A = l × w
208 = 13 × w
w = 208/13
w = 16 feet
Question 7.
Zoe is saving money to go on a trip to Mexico. She earns $16.75 for mowing the lawn. If Zoe mows the lawn 28 times, how much money will she earn?
Solve the problem:
What strategy did you use? Why?
Answer:
Given,
Zoe is saving money to go on a trip to Mexico. She earns $16.75 for mowing the lawn.
$16.75 × 28 = $469
Thus she earns $469.
Question 8.
Briana is making a box for her art supplies. The box has a base of 176 square inches. The height of the box is 26 inches. What is the volume of the box?
Solve the problem:
What strategy did you use? Why?
Answer:
Given,
Briana is making a box for her art supplies.
The box has a base of 176 square inches.
The height of the box is 26 inches.
176 × 26 = 4576 cu. inches
Thus the volume of the box is 4576 cu. inches.
Leah’s Problems
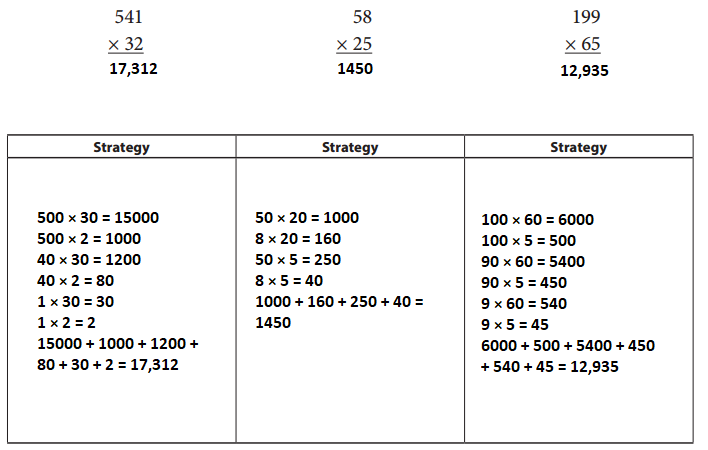
Question 1.
Leah needs to solve the three problems below. She has to use the standard algorithm for multiplication at least once. For each problem, decide which strategy Leah should use and then solve the problem.

Answer:
Question 2.
Leah solved 302 × 67 by multiplying 300 by 60 and 2 by 7 and adding those products together. Did she get the right answer? Why or why not?
Answer:
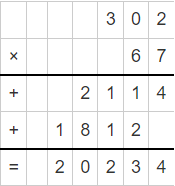
300 × 60 = 18000
2 × 60 = 120
300 × 7 = 2100
2 × 7 = 14
18000 + 120 + 2100 + 14 = 20,234
Review
Question 3.
What is \(\frac{3}{4}\) of 96?
Answer:
Given,
\(\frac{3}{4}\) of 96
= \(\frac{3}{4}\) × 96
= 3 × 24
= 72
So, \(\frac{3}{4}\) of 96 is 72.
Question 4.
What is \(\frac{4}{5}\) of 80?
Answer:
\(\frac{4}{5}\) of 80
= \(\frac{4}{5}\) × 80
= 4 × 16
= 64
So, \(\frac{4}{5}\) of 80 is 64.
Question 5.
What is \(\frac{2}{3}\) of 45?
Answer:
\(\frac{2}{3}\) of 45
= \(\frac{2}{3}\) × 45
= 2 × 15
= 30
So, \(\frac{2}{3}\) of 45 is 30.