Students looking for the Bridges in Mathematics Grade 5 Student Book Answer Key Unit 1 Module 2 can find a better approach to solve the problems.
Bridges in Mathematics Grade 5 Student Book Answer Key Unit 1 Module 2
Bridges in Mathematics Grade 5 Student Book Unit 1 Module 2 Session 1 Answer Key
Are They Equivalent?
Question 1.
Mark each of the following equations as true or false and tell how you know.
a. 12 × 6 = 24 × 3 _______________
Answer:
True
Explanation:
12 × 6 = 72
24 × 3 = 72
12 × 6 = 24 × 3
72 = 72
So, LHS = RHS
Hence, it is true.
b. 7 × 4 = 28 × 2 _______________
Answer:
False
Explanation:
7 × 4 = 28
28 × 2 = 56
7 × 4 ≠ 28 × 2
28 ≠ 56
c. 48 × 6 = 24 × 3 ________________
Answer:
False.
Explanation:
48 × 6 = 288
24 × 3 = 72
48 × 6 ≠ 24 × 3
288 ≠ 72
d. 16 × 4 = 2 × 32 ________________
Answer:
True
Explanation:
16 × 4 = 64
2 × 32 = 64
64 = 64
16 × 4 = 2 × 32
So, LHS = RHS
Hence, it is true.
e. (22 × 7) × 59 = 22 × (7 × 59) _______________
Answer:
True
Explanation:
(22 × 7) × 59 = 22 × (7 × 59)
(22 × 7) × 59 = 22 × (7 × 59)
154 x 59 = 22 x 413
9,086 = 9, 086
(22 × 7) × 59 = 22 × (7 × 59)
So, LHS = RHS
Hence, it is true.
Question 2.
Fill in the blank to make each equation true.
a. 6 × ___________ = 3 × 14
Answer:
7
Explanation:
Given,
6 × ___________ = 3 × 14
6 × ___ = 42
42 ÷ 6 = 7
6 × 7 = 42
b. 8 × 5 = 4 × ____________
Answer:
10
Explanation:
Given,
8 × 5 = 4 × _____
40 ÷ 4 = 10
4 × 10 = 40
c. 12 × 16 = ____________ × 8
Answer:
24
Explanation:
Given,
12 × 16 = ____________ × 8
192 ÷ 8 = 24
8 x 24 = 192
d. ____________ × 8 = 16 × 2
Answer:
4
Explanation:
Given,
____________ × 8 = 16 × 2
16 × 2 = 32
32 ÷ 8 = 4
4 × 8 = 32
e. 4 × _____________ = 2 × 26
Answer:
13
Explanation:
Given,
4 × _____________ = 2 × 26
2 × 26 = 52
52 ÷ 4 = 13
4 × 13 = 52
Question 3.
CHALLENGE Thao says she can find the answer to 8 × 90 by halving the 8 and doubling the 90 again and again until she gets down to 1 × 720. Is she correct? Prove your answer.
Answer:
Yes, she is correct.
Explanation:
Given that,
Thao says she can find the answer to 8 × 90 by halving the 8 and doubling the 90 again and again until she gets down to 1 × 720.
8 × 90 = 720
4 × 180 = 720
2 × 360 = 720
1 × 720 = 720
Bridges in Mathematics Grade 5 Student Book Unit 1 Module 2 Session 2 Answer Key
Smaller Boxes
Brad needs some boxes to hold his smaller orders of 12 baseballs.
Question 1.
List all the possible boxes that could hold 12 balls, if each ball takes up a 1 × 1 × 1 space. You can use numbers, labeled sketches, or words to show, but try to use a system where you can be sure you’ve found all the different boxes.
Answer:
4 × 1 × 3 or 3 × 1 × 4
Explanation:
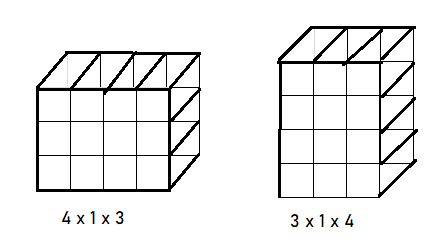
To hold 12 balls, if each ball takes up a 1 × 1 × 1 space.
4 × 1 × 3 can hold 12 balls or 3 × 1 × 4 can hold 12 balls
Question 2.
Match each expression with the correct box below.
The numbers in parentheses represent the dimensions of the base and the third number represents the height (number of layers).
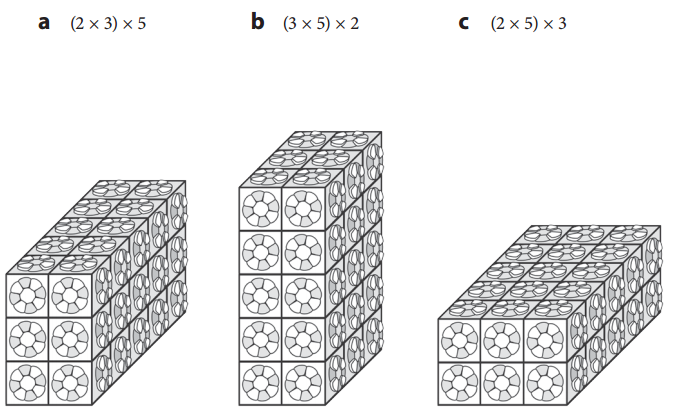
Answer:
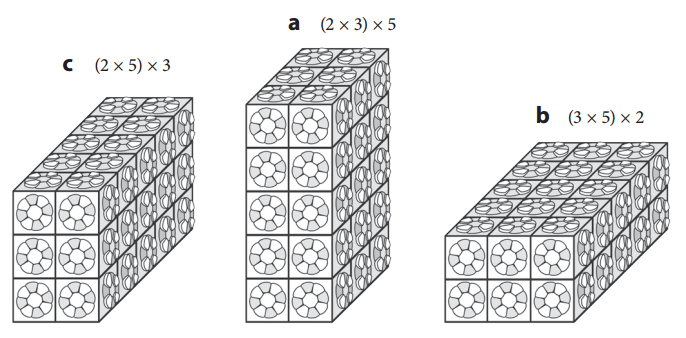
Explanation:
The numbers in parentheses represent the dimensions of the base and the third number represents the height (number of layers).
First image is base of (2 × 5) height 3
Second image is base of (2 × 3) height 5
Third image is base of (3 × 5) height 2
Bridges in Mathematics Grade 5 Student Book Unit 1 Module 2 Session 3 Answer Key
Calculating Cardboard
Below is a list of six possible box designs for Brad’s 24 baseballs. Determine how many units of cardboard are needed to construct each box.
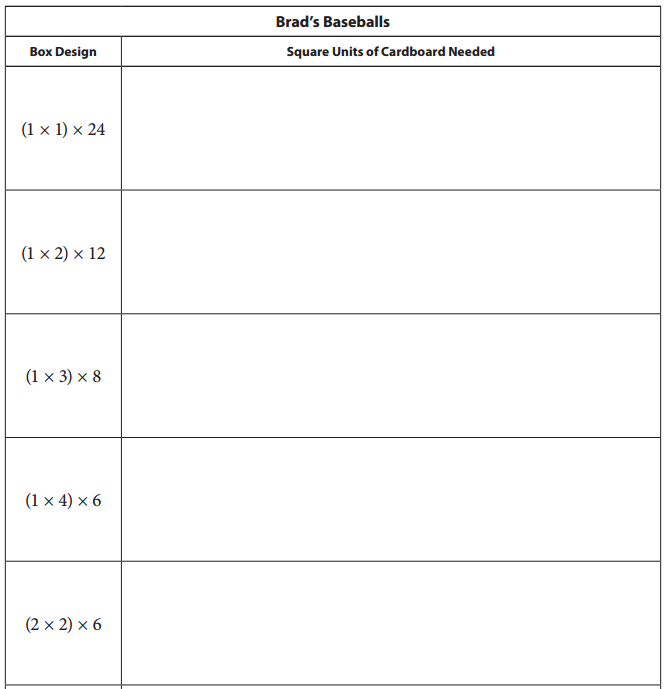

Answer:
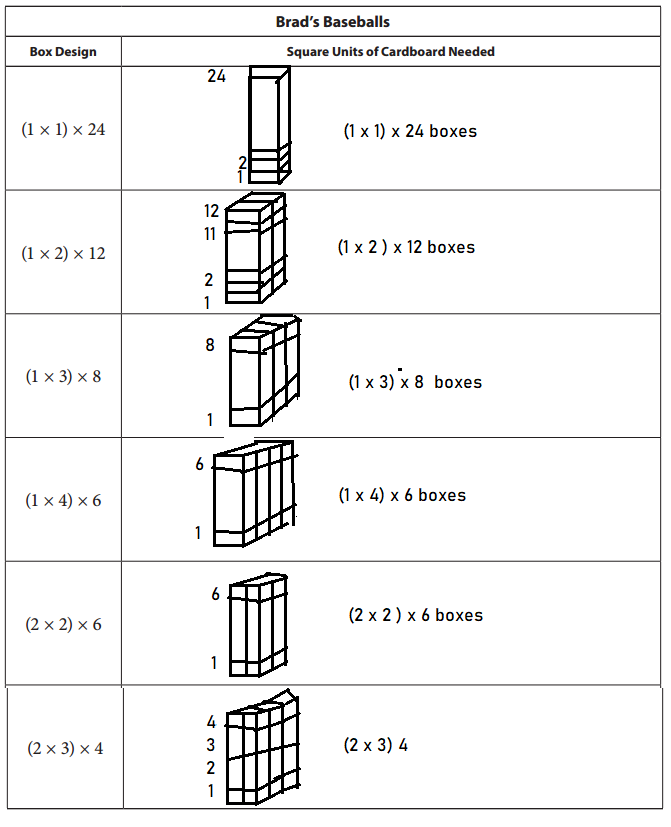
Explanation:
six possible box designs for Brad’s 24 baseballs.
1 × 1 cuboid of 24 boxes units of cardboard are needed to construct each box to hold 24 base balls.
1 × 2 cuboid of 12 boxes units of cardboard are needed to construct each box to hold 24 base balls.
1 × 3 cuboid of 8 boxes units of cardboard are needed to construct each box to hold 24 base balls.
1 × 4 cuboid of 6 boxes units of cardboard are needed to construct each box to hold 24 base balls.
2 × 2 cuboid of 6 boxes units of cardboard are needed to construct each box to hold 24 base balls.
2 × 3 cuboid of 4 boxes units of cardboard are needed to construct each box to hold 24 base balls.
Zack’s Strategies
Zack has been working with a variety of multiplication strategies.
Question 1.
Write an expression to describe each of the statements Zack made.
a. To solve 24 × 15, I double and halve.
Answer:
24 × 15 = 360
12 × 30 = 360
Explanation:
24 × 15 = 360
double the 15
15 × 2 = 30
24 halve 2 = 12
12 × 30 = 360
b. To solve 14 × 8, I find 14 × 10 and remove 2 groups of 14.
Answer:
14 × 8 = 112
Explanation:
14 × 8 = 112
14 × 10 = 140
remove 2 groups of 14 = 14 × 2 = 28
So, 140 – 28 = 112
Question 2.
Evaluate the two expressions above (in other words, find the values).
a. 14 × 8 = 112
b. 14 × 10 = 140
Answer:
To solve 14 × 8, I find 14 × 10 and add 2 groups of 14.
Explanation:
14 × 8 = 112
14 × 10 = 140
14 × 2 = 28
112 + 28 = 140
Question 3.
Fill in the blanks.
a. (2 × 3) × ____________ = 30
Answer:
6
Explanation:
Given,
(2 × 3) × ____________ = 30
6 × ____________ = 30
30 ÷ 6 = 5
5 × 6 = 30
So, (2 × 3) × 6 = 5 × 6 = 30
b. 4 × (____________ × 4) = 48
Answer:
3
Explanation:
Given,
4 × (____________ × 4) = 48
16 x = 48
x = 48 ÷ 16
x = 3
So, 4 × 3 × 4 = 4 × (3 × 4) = 4 × 12 = 48
Question 4.
True or False?
a. 4 × 9 = (4 × 10) – 1 _____________
Answer:
False
Explanation:
Given,
4 × 9 = (4 × 10) – 1 _____________
36 = 40 – 1
36 ≠ 39
So, 4 × 9 ≠ (4 × 10) – 1
b. 9 × 13 = (10 × 13) – (1 × 9) _____________
Answer:
False.
Explanation:
Given,
9 × 13 = (10 × 13) – (1 × 9)
117 = 130 – 9
117 ≠ 121
So, 9 × 13 ≠ (10 × 13) – (1 × 9)
Question 5.
Solve the following.
a. 9 × 3 = ________________
9 × 30 = ______________
Answer:
270
Explanation:
Given,
9 × 3 = ________________
9 × 30 =
9 × 3 = 27
9 × 30 = 270
30 is written as 10 × 3
So, the equation is 9 × 3 × 10 = 9 × 30 = 270
b. 15 × 4 = ______________
15 × 40 = _____________
Answer:
60
Explanation:
Given,
15 × 4 = ______________
15 × 40 =
15 × 4 = 60
15 × 40 = 600
40 is written as 4 × 10
So, the equation is 15 × 4 × 10 = 15 × 40 = 600
Bridges in Mathematics Grade 5 Student Book Unit 1 Module 2 Session 4 Answer Key
How many boxes?
Question 1.
Shane is making boxes to hold baseballs. He wants the dimensions to be 3 × 5 × 7 units. How many balls can one of Shane’s boxes hold?
Answer:
105 baseballs.
Explanation:
Given that,
Shane wants the dimensions of baseballs to be 3 × 5 × 7 units.
Total balls can one of Shane’s boxes hold,
(3 × 5) = 15 base balls
(3 × 5) × 7 = 15 × 7 = 105 baseballs.
Question 2.
Riley is also making boxes to hold baseballs. She wants the dimensions of her boxes to be 4 × 6 × 3 units. How many balls can one of Riley’s boxes hold?
Answer:
72 baseballs.
Explanation:
Given that,
Riley wants the dimensions of her boxes to be 4 × 6 × 3 units.
Total balls can one of Riley’s boxes hold,
(4 × 6) = 24 base balls
(4 × 6) × 3 = 24 × 3 = 72 baseballs.
Question 3.
Raquel found two boxes in her storeroom. One box has the dimensions 6 × 2 × 3 and the other is 2 × 3 × 6. Which box holds more balls? Explain your thinking.
Answer:
Both boxes can hold the same number of base balls.
Explanation:
Given that,
Raquel found one box has the dimensions 6 × 2 × 3,
the other is 2 × 3 × 6.
(6 × 2) = 12 base balls.
(6 × 2) × 3 = 12 × 3 = 36 base balls.
(2 × 3) = 6 base balls.
(2 × 3) × 6 = 6 × 6 = 36 base balls.
So, both boxes can hold the same number of base balls.
Bridges in Mathematics Grade 5 Student Book Unit 1 Module 2 Session 5 Answer Key
Work Place Instructions 1B The Multiple Game
Each pair of players needs:
- 2 colored pencils of different colors
- a 1B Multiple Game Record Sheet to share
1. Player 1 chooses a target number on the game board by drawing a circle around it. This number represents Player 1’s points for this round.
2. Using a different color, Player 2 circles all the numbers on the board for which the target number is a multiple, not including the target number itself. Player 2 adds these numbers together. The sum is Player 2’s points for this round.
For example, if Player 1 chooses 12 as a target number, Player 2 would circle 1, 2, 3, 4, and 6 because 12 is a multiple of each. So, Player 1 has 12 points and Player 2 has 16 points so far.

3. Then, Player 2 chooses and circles a new target number, and Player 1 circles all the numbers for which Player 1’s target is a multiple. Once a number on the game board has been circled, it may no longer be used.
4.Players take turns choosing target numbers and circling factors.
If a player chooses a target number for which there are no factors that can still be circled, that number must be crossed out and the player does not get points for that turn.
5. When the numbers remaining are not multiples of any un circled numbers (i.e., when no further plays can be made) the game is over.
6. Each player then finds the sum of the numbers that are circled with her color. The player with the greater total is the winner.
Game Variations
A. A pair of players may play against another pair.
B. Players may create a game board that contains numbers greater than 30.
Milo’s Multiples
Question 1.
Help Milo find at least three multiples for each number below.
a. 12: __________, __________, __________
Answer:
12: 24, 36, 48
Explanation:
The three multiples for the number 12 are:
12 × 2 = 24
12 × 3 = 36
12 × 4 = 48
b. 16: __________, __________, __________
Answer:
16: 32, 48, 64
Explanation:
The three multiples for the number 16 are:
16 × 2 = 32
16 × 3 = 48
16 × 4 =64
c. 23: __________, __________, __________
Answer:
23: 46, 69, 92
Explanation:
The three multiples for the number 23 are:
23 × 2 = 46
23 × 3 = 69
23 × 4 = 92
Question 2.
Help Milo find the factors of each of the numbers below.
a. 12: __________, __________, __________, __________, __________, __________
Answer:
The factors of 12 are 1, 2, 3, 4, 6 and 12.
Explanation:
A factor is a number that divides another number, leaving no remainder.
The factors of 12 are 1, 2, 3, 4, 6 and 12
1 × 12 = 12
2 × 6 = 12
3 × 4 = 12
6 × 3 = 12
12 × 1 = 12
b. 16: __________, __________, __________, __________, __________
Answer:
The factors of 16: 1, 2, 4, 8 and 16.
Explanation:
A factor is a number that divides another number, leaving no remainder.
The factors of 16: 1, 2, 4, 8 and 16.
1 × 16 = 16
2 × 8 = 16
4 × 4 = 16
16 × 1 = 16
c. 23: __________, __________
Answer:
Factors of 23: 1 and 23
Explanation:
A factor is a number that divides another number, leaving no remainder.
1 × 23 = 23
23 × 1 = 23
d. 36: __________, __________, __________, __________, __________, __________, __________, __________, __________
Answer:
The factors of 36 are 1, 2, 3, 4, 6, 9, 12,18 and 36.
Explanation:
A factor is a number that divides another number, leaving no remainder.
1 × 36 = 36
2 × 16 = 36
3 × 12 = 36
4 × 9 = 36
6 × 6 = 36
12 × 3 = 36
18 × 2 = 36
36 × 1 = 36
Question 3.
What factors do 16 and 24 have in common?
Answer:
1, 2, 4 and 8 are common factors.
Explanation:
A factor is a number that divides another number, leaving no remainder.
The factors of 16: 1, 2, 4, 8 and 16.
The factors of 24: 1, 2, 3, 4, 6, 8, 12 and 24.
So, factors of 16 and 24 have in common are 1, 2, 4 and 8
Question 4.
What are two multiples that 8 and 16 have in common?
Answer:
1, 2 , 4 and 8
Explanation:
A factor is a number that divides another number, leaving no remainder.
The factors of 8: 1, 2, 4 and 8
The factors of 16: 1, 2, 4, 8 and 16.
So, the common factors in both are 1, 2 , 4 and 8.
Question 5.
CHALLENGE Farah’s mom told her she’s thinking of a number that is a multiple of 12. What else can Farah say with certainty about the number her mom is thinking of?
Answer:
Yes, Farah can say with certainty about the number her mom is thinking of is greater than or equal to 12.
Explanation:
Given that, the number is a multiple of 12.
let the number be 12x,
So, Farah can say with certainty about the number her mom is thinking of is greater than or equal to 12
Bridges in Mathematics Grade 5 Student Book Unit 1 Module 2 Session 6 Answer Key
Thinking About The Multiple Game
Question 1.
List the factors for each number below. Write P next to numbers that are prime and C next to numbers that are composite.
a. 29: _____________
Answer:
29 P
Explanation:
The factors of 29 is 1 and 29.
1 × 29 = 29
29 × 1 = 29
As, 29 is a prime number.
b. 25: ______________
Answer:
25 C
Explanation:
The factors of 25 is 1, 5 and 25.
1 × 25 = 25
5 × 5 = 25
25 × 1 = 25
As, 25 is a composite number.
c. 24: ______________
Answer:
24 C
Explanation:
The factors of 24 is 1, 2, 3, 4, 6, 8 and 24.
1 × 24 = 24
2 × 12 = 24
3 × 8 = 24
4 × 6 = 24
6 × 4 = 24
8 × 3 = 24
24 × 1 = 24
As, 24 is a composite number.
d. 23: _______________
Answer:
23 P
Explanation:
The factors of 23 is 1 and 23.
1 × 23 = 23
23 × 1 = 23
As, 23 is a prime number.
Question 2.
Which of the above numbers would you choose if you were going first in The Multiple Game? Why?
Answer:
24, It has more factors for Multiple Game.
Explanation:
The factors of 24 is 1, 2, 3, 4, 6, 8 and 24.
1 × 24 = 24
2 × 12 = 24
3 × 8 = 24
4 × 6 = 24
6 × 4 = 24
8 × 3 = 24
24 × 1 = 24
24 is a composite number.
Question 3.
In The Multiple Game, when would be a good time to choose the number 30?
Answer:
30 factors are 1, 2, 3, 5, 6,10, 15 and 30.
Explanation:
It has more factors for Multiple Game
30 factors are 1, 2, 3, 5, 6,10, 15 and 30.
1 × 30 = 30
2 × 15 = 30
3 × 10 = 30
5 × 6 = 30
6 × 5 = 30
10 × 3 = 30
15 × 2 = 30
Question 4.
Write an expression for each of the calculations below.
a. Multiply 3 by 6, and divide by 9.
Answer:
2
Explanation:
Given,
Multiply 3 by 6, and divide by 9.
(3 × 6) ÷ 9
= 18 ÷ 9
= 2
b. Subtract 10 from 30, and then multiply by 20.
Answer:
400
Explanation:
Given,
Subtract 10 from 30, and then multiply by 20.
30 – 10 = 20
20 × 20 = 400
c. Add 13 and 17 and 21, and multiply the sum by 25.
Answer:
1,275
Explanation:
Given,
Add 13 and 17 and 21, and multiply the sum by 25.
(13 + 17 + 21) × 25
= 51 × 25
=1,275
d. Divide 36 by 4, then add 45.
Answer:
54
Explanation:
Given,
Divide 36 by 4, then add 45
36 ÷ 4 = 9
9 + 45 = 54