Students looking for the Bridges in Mathematics Grade 5 Home Connections Answer Key Unit 6 Module 4 can find a better approach to solve the problems.
Bridges in Mathematics Grade 5 Home Connections Answer Key Unit 6 Module 4
Bridges in Mathematics Grade 5 Home Connections Unit 6 Module 4 Session 2 Answer Key
Abby’s Arrays
Question 1.
Abby is setting up an array to solve 1\(\frac{3}{4}\) × 2\(\frac{1}{2}\).
a. Fill in the blanks on the array.
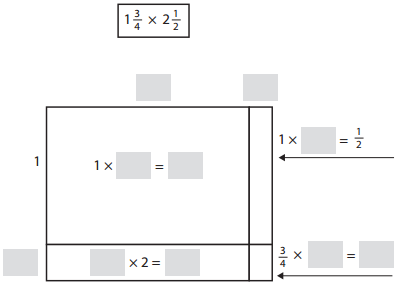
Answer:
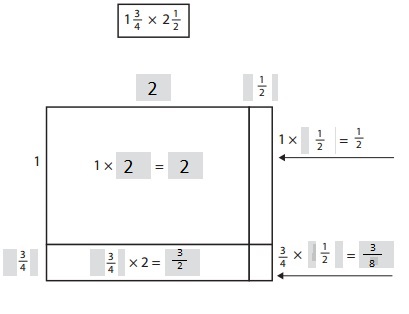
Explanation:
Given Abby is setting up an array to solve 1\(\frac{3}{4}\) X 2\(\frac{1}{2}\) = \(\frac{16}{8}\) + \(\frac{4}{8}\) + \(\frac{12}{8}\) + \(\frac{3}{8}\) = \(\frac{35}{8}\), Filled in the blanks on the array above.
b. Fill in the blanks: 1\(\frac{3}{4}\) × 2\(\frac{1}{2}\) = __________ + __________ + __________ + __________ = __________
Answer:
\(\frac{16}{8}\) + \(\frac{4}{8}\) + \(\frac{12}{8}\) + \(\frac{3}{8}\) = \(\frac{35}{8}\),
Explanation:
Asked to fill in the blanks : 1\(\frac{3}{4}\) X 2\(\frac{1}{2}\) = \(\frac{1 X 4 + 3}{4}\) × 2\(\frac{1}{2}\) upon solving \(\frac{1 X 4}{4}\) + \(\frac{3}{4}\) X \(\frac{2 X 2}{2}\) + \(\frac{1}{2}\) = \(\frac{4}{4}\) + \(\frac{3}{4}\) X \(\frac{4}{2}\) + \(\frac{1}{2}\) = 1 + \(\frac{3}{4}\) X 2 + \(\frac{1}{2}\) = 1 X 2 + 1 X \(\frac{1}{2}\) + \(\frac{3}{4}\) X 2 + \(\frac{3}{4}\) X \(\frac{1}{2}\) =
2 + \(\frac{1}{2}\) + \(\frac{6}{4}\) + \(\frac{3 X 1}{4 X 2}\) =
2 + \(\frac{1}{2}\) + \(\frac{3}{2}\) + \(\frac{3}{8}\) or we take common denominator as \(\frac{16}{8}\) + \(\frac{4}{8}\) + \(\frac{3 X 4}{8}\) + \(\frac{3}{8}\) = \(\frac{16}{8}\) + \(\frac{4}{8}\) + \(\frac{12}{8}\) + \(\frac{3}{8}\) = \(\frac{35}{8}\).
Question 2.
Abby needs to solve 2\(\frac{1}{2}\) × 3\(\frac{2}{5}\).
a. Sketch and label an array that shows 2\(\frac{1}{2}\) × 3\(\frac{2}{5}\).
Answer:
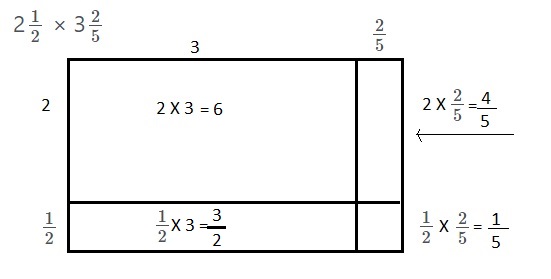
Explanation:
Sketched and labeled an array that shows 2\(\frac{1}{2}\) X 3\(\frac{2}{5}\) above.
b. Use your sketch to solve the problem.
2\(\frac{1}{2}\) × 3\(\frac{2}{5}\) = __________ + __________ + __________ + __________ = __________
Answer:
6 + \(\frac{4}{5}\) + \(\frac{3}{2}\) + \(\frac{1}{5}\) = \(\frac{17}{2}\),
Explanation:
Using my sketch to solve the problem as 2\(\frac{1}{2}\) X 3\(\frac{2}{5}\) = \(\frac{2 X 2 + 1}{2}\) X \(\frac{3 X 5 + 2}{5}\) = \(\frac{4}{2}\) + \(\frac{1}{2}\) X \(\frac{15}{5}\) + \(\frac{2}{5}\) = 2 + \(\frac{1}{2}\) X 3 + \(\frac{2}{5}\) = 2 X 3 + 2 X \(\frac{2}{5}\) + \(\frac{1}{2}\) X 3 + \(\frac{1}{2}\) X \(\frac{2}{5}\) = 6 + \(\frac{2 X 2}{5}\) + \(\frac{1 X 3}{2}\) + \(\frac{1 X 2}{2 X 5}\) = 6 + \(\frac{4}{5}\) + \(\frac{3}{2}\) + \(\frac{1}{5}\) taking common denominator we get \(\frac{6 X 10}{10}\) + \(\frac{2 X 4}{10}\) + \(\frac{3 X 5}{2}\) + \(\frac{1 X 2}{5}\) = \(\frac{60 + 8 + 15 + 2}{10}\) = \(\frac{85}{10}\) both goes in 5 we get \(\frac{17 X 5}{2 X 5}\) = \(\frac{17}{2}\).
Question 3.
Use doubling and halving to fill in the blanks and solve the problems.
a. 5\(\frac{1}{4}\) × 12 = ___________ × 6 = ____________
Answer:
5\(\frac{1}{4}\) X 12 = \(\frac{21}{2}\) X 6 = 63,
Explanation:
Using doubling and halving to fill in the blanks as 5\(\frac{1}{4}\) X 12 = \(\frac{4 X 5 + 1}{4}\) X 12 = \(\frac{21}{4}\) X 12 = \(\frac{21}{2}\) X 6 = 21 X 3 = 63.
b. 16 × 3\(\frac{1}{2}\) = 8 × ____________ = ____________
Answer:
8 X 7 = 56,
Explanation:
Using doubling and halving to fill in the blanks as 16 X 3\(\frac{1}{2}\) = 16 X \(\frac{2 x 3 + 1}{2}\) = 8 X 7 = 56.
c. 36 × ___________ = 18 × 9 = ____________
Answer:
36 X 4\(\frac{1}{2}\) = 18 X 9 = 162,
Explanation:
Given to solve 36 X x = 18 X 9, so we get x = \(\frac{18 X 9}{36}\) = \(\frac{9}{2}\) as numerator is greater than denominator we write as \(\frac{4 X 2 + 1}{2}\) = 4\(\frac{1}{2}\) therefore the result is 36 X 4\(\frac{1}{2}\) = 18 X 9 = 162.
d. 15 × 6\(\frac{2}{3}\) = _____________ × 3\(\frac{1}{3}\) = _____________
Answer:
15 X 6\(\frac{2}{3}\) = 30 X 3\(\frac{1}{3}\) = 100,
Explanation:
Given to solve let it be x so15 X 6\(\frac{2}{3}\) = x X 3\(\frac{1}{3}\) we get x X \(\frac{3 X 3 + 1}{3}\) = 15 X \(\frac{6 X 3 + 2}{3}\), x X \(\frac{10}{3}\) = 15 X \(\frac{20}{3}\), x = \(\frac{15 X 20 X 3}{3 X 10}\) = 30 as x = 30 we get the equation as 15 X 6\(\frac{2}{3}\) = 30 X 3\(\frac{1}{3}\) = 100.
Question 4.
Adam made a birthday card for his sister. The rectangular card was 6\(\frac{1}{2}\) inches by 9\(\frac{1}{3}\) inches. What is the area of the birthday card? Make a labeled sketch to model and solve this problem. Show all of your work.
Answer:
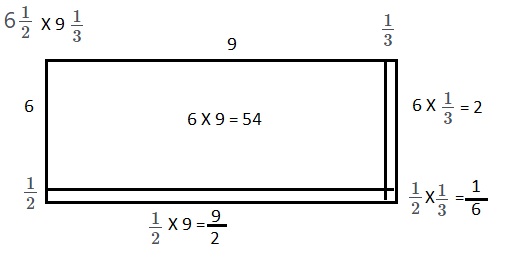
The area of the birthday card is \(\frac{182}{3}\) square inches or 60\(\frac{2}{3}\) square inches,
Explanation:
Given Adam made a birthday card for his sister. The rectangular card was 6\(\frac{1}{2}\) inches by 9\(\frac{1}{3}\) inches. Made a labeled sketch to model and the area of the birthday card is 6\(\frac{1}{2}\) inches X 9\(\frac{1}{3}\) inches = \(\frac{6 X 2 + 1}{2}\) inches by \(\frac{9 X 3 + 1}{3}\) inches = \(\frac{13}{2}\) inches X \(\frac{28}{3}\) inches = \(\frac{13 X 28}{2 X 3}\) square inches \(\frac{13 X 14}{3}\) square inches = \(\frac{182}{3}\) square inches as numerator is greater than denominator we write as \(\frac{60 X 3 + 2}{3}\) square inches = 60\(\frac{2}{3}\) square inches.
Question 5.
Convert these fractions to decimals.
a. \(\frac{8}{10}\) = 0. _____________
Answer:
0.8,
Explanation:
Asked to convert the fraction into decimal so it is
10)8(0.8
8
0
therefore \(\frac{8}{10}\) = 0.8.
b. \(\frac{3}{4}\) = 0. _____________
Answer:
0.75,
Explanation:
Asked to convert the fraction into decimal so it is
4)3(0.75
2.8
0.20
0.20
0
therefore \(\frac{3}{4}\) = 0.75.
c. \(\frac{4}{5}\) = 0. ______________
Answer:
0.8,
Explanation:
Asked to convert the fraction into decimal so it is
5)4(0.8
4.0
0
therefore \(\frac{4}{5}\) = 0.8.
d. \(\frac{6}{5}\) = ___________. ___________
Answer:
1.2
Explanation:
Asked to convert the fraction into decimal so it is
5)6(1.2
5
1.0
1.0
0
therefore \(\frac{6}{5}\) = 1.2.
Question 6.
CHALLENGE Justin got a sack of jelly beans in 5 different colors. Half of them were red, \(\frac{1}{6}\) were green, \(\frac{1}{6}\) were yellow, \(\frac{1}{12}\) were orange, and 6 were black. How many of each color did he get, and how many jelly beans were there in all? Show your work.
Answer:
Number of red jelly beans are 36,
Number of green jelly beans are 12,
Number of yellow jelly beans are 12,
Number of orange jelly beans are 6,
Number of black jelly beans are 6, Total number of jelly beans are 72,
Explanation:
Given Justin got a sack of jelly beans in 5 different colors. Half of them were red, \(\frac{1}{6}\) were green, \(\frac{1}{6}\) were yellow, \(\frac{1}{12}\) were orange and 6 were black let us take the total number of beans as x so
\(\frac{x}{2}\) + \(\frac{x}{6}\) + \(\frac{x}{6}\) + \(\frac{x}{12}\) + 6 = x, we take common denominator 12 X \(\frac{x}{2}\) + 12 X \(\frac{x}{6}\) + 12 X \(\frac{x}{6}\) + 12 X \(\frac{x}{12}\) + 12 X 6 = 12 X x further we get 6x + 2x + 2x + x + 72 = 12x combining like terms 11x + 72 = 12x
so 72 = 12 x – 11x = x, therefore x = 72, Number of red jelly beans are \(\frac{72}{2}\) = 36, Number of green jelly beans are \(\frac{72}{6}\) = 12,
Number of yellow jelly beans are \(\frac{72}{6}\) = 12,
Number of orange jelly beans are \(\frac{72}{12}\) = 6 and Number of black jelly beans are 6 respectively.
Bridges in Mathematics Grade 5 Home Connections Unit 6 Module 4 Session 3 Answer Key
Unit 6 Review
Use the diagrams below to answer the following questions.
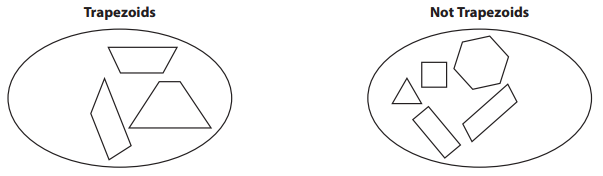
Question 1.
List three properties of a trapezoid.
Answer:
Three properties of trapezoid: 1. The bases are parallel to each other. 2. Sum of all the angles in a trapezoid is equal to 360 degrees, 3. The sum of the angles on the same side is equal to 180 degrees,
Explanation:
A trapezoid is also known as a trapezium is a four-sided polygon or a quadrilateral. It has one set of opposite sides which are parallel and a set of non-parallel sides. The parallel sides are known as the bases and the non-parallel sides are known as the legs of the trapezoid.
Three properties of trapezoid: 1. The bases are parallel to each other. 2. Sum of all the angles in a trapezoid is equal to 360 degrees, 3. The sum of the angles on the same side is equal to 180 degrees.
Question 2.
Fill in the bubbles beside all the other names you could use for a trapezoid.
quadrilateral
triangle
rectangle
polygon
Answer:
Explanation:
A trapezoid is also known as a trapezium is a four-sided polygon or a quadrilateral. It has one set of opposite sides which are parallel and a set of non-parallel sides. Trapezoid cannot be a triangle as it has 4 sides and It can be a rectangle if its opposite sides are equal in length and at right angles to each other. So, all rectangles are trapezoids, but, not all trapezoids are rectangles. Therefore filled the bubbles beside quadrilateral and polygon above.
Question 3.
Explain why a trapezoid can’t be called a parallelogram.
Answer:
No, a trapezoid cannot be a parallelogram,
Explanation:
Trapezoid has only one pair of parallel sides while in a parallelogram there are two pairs of parallel sides.
Question 4.
While playing Polygon Search, Shana graphed the points (1, 2), (4, 2), (4, 5) and (1, 5).
a. Graph the ordered pairs.
Answer:
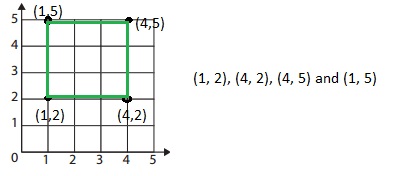
Explanation:
Given while playing Polygon Search, Shana graphed the points (1, 2), (4, 2), (4, 5) and (1, 5).
Graphed the ordered pairs as shown above.
b. Name the shape that Shana drew.
Answer:
Square,
Explanation:
By using the graph it shows all the side lengths of 3 units each so its the square shape.
c. List 2 properties of this shape.
Answer:
Properties:
1. All four interior angles are equal to 90 degrees, 2. All four sides of the square are congruent or equal to each other,
Explanation:
Two properties of the square shape is 1. All four interior angles are equal to 90 degrees, 2. All four sides of the square are congruent or equal to each other.
Question 5.
Cooper and Luke each made a sequence with tiles. Then they graphed their sequences on the same coordinate grid.
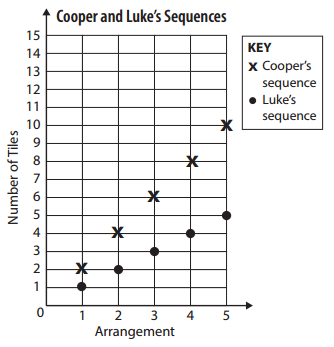
a. List the first 5 ordered pairs of Cooper’s sequence:
Answer:
Explanation:
Listed above the first 5 ordered pairs of Cooper’s sequence.
b. List the first 5 ordered pairs of Luke’s sequence:
Answer:
Explanation:
Listed above the first 5 ordered pairs of Luke’s sequence.
c. What can you tell about the boys’ tile sequences from looking at the graph they made? Fill in the bubbles beside all the correct observations.
Cooper used twice as many tiles as Luke in each arrangement.
Cooper started with 3 tiles and added 2 more tiles for each new arrangement.
Luke’s third arrangement had 6 tiles.
There would be 12 tiles in Cooper’s sixth arrangement.
Answer:
Explanation:
As Cooper and Luke each made a sequence with tiles. Then they graphed their sequences on the same coordinate grid. After seeing the boys’ tile sequences from looking at the graph they made we can conclude that Cooper used twice as many tiles as Luke in each arrangement so filled in the bubbles beside the correct observations as shown above.
Question 6.
A packing box is 3 feet wide, 5 feet long, and 8 feet high. What is its volume? Show your work.
Answer:
Volume is 120 cubic feet,
Explanation:
Given a packing box is 3 feet wide, 5 feet long, and 8 feet high so its volume is 3 feet X 5 feet X 8 feet = 120 cubic feet.
Question 7.
Shanti keeps her school supplies in a little container with a base that is 7″ by 7″. The volume of the container is 343 cubic inches.
a. What is the height of the container? Show your work.
Answer:
Height of the container is 7 inches,
Explanation:
Given Shanti keeps her school supplies in a little container with a base that is 7″ by 7″. The volume of the container is 343 cubic inches. As we know volume of container = length X width X height we have 343 cubic inches = 7 inches X 7 inches X height, therefore height = 343 cubic inches/ 7 inches X 7 inches = 7 inches.
b. What shape is the container? How do you know?
Answer:
Cube, All sides are equal,
Explanation:
The shape of the container is cube because all of its sides are equal of 7 inches, As we know a cube is a shape multiplied by itself three times.