Students looking for the Bridges in Mathematics Grade 5 Home Connections Answer Key Unit 2 Module 4 can find a better approach to solve the problems.
Bridges in Mathematics Grade 5 Home Connections Answer Key Unit 2 Module 4
Bridges in Mathematics Grade 5 Home Connections Unit 2 Module 4 Session 1 Answer Key
Find the Greater Fraction
Question 1.
Find the least common multiple for each pair of numbers. Show all your work.
ex 3 and 5
3: 3, 6, 9, 12, ![]() 18
18
5: 5, 10, ![]() 20
20
The LCM is 15.
a. 4 and 6
Answer:
4: 4, 8, 12, 16, 20, 24, 28, 32
6: 6, 12, 18, 24
The LCM is 12.
b. 3 and 7
Answer:
3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
7: 7, 14, 21, 28, 35
The LCM is 21.
c. 5 and 8
Answer:
5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
8: 8, 16, 24, 32, 40, 48
The LCM is 40.
d. 6 and 9
Answer:
6: 6, 12, 18, 24, 30
9: 9, 18, 27, 36
The LCM is 18.
Question 2.
Use the least common multiple to find equivalent fractions for each fraction pair. Then, use the symbol < or > to show the bigger fraction.
ex \(\frac{3}{4}\) and \(\frac{4}{6}\)
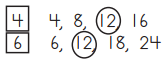
\(\frac{3}{4}\) = \(\frac{3 \times 3}{4 \times 3}\) = \(\frac{9}{12}\) \(\frac{4}{6}\) = \(\frac{4 \times 2}{6 \times 2}\) = \(\frac{8}{12}\)
\(\frac{9}{12}\) > \(\frac{8}{12}\) so \(\frac{3}{4}\) > \(\frac{4}{6}\)
a. \(\frac{5}{8}\) and \(\frac{2}{3}\)
Answer:
\(\frac{5}{8}\) and \(\frac{2}{3}\)
\(\frac{5}{8}\) × \(\frac{3}{3}\) = \(\frac{15}{24}\)
\(\frac{2}{3}\) × \(\frac{8}{8}\) = \(\frac{16}{24}\)
\(\frac{15}{24}\) < \(\frac{16}{24}\)
b. \(\frac{1}{6}\) and \(\frac{2}{9}\)
Answer:
\(\frac{1}{6}\) and \(\frac{2}{9}\)
\(\frac{1}{6}\) × \(\frac{9}{9}\) = \(\frac{9}{54}\)
\(\frac{2}{9}\) × \(\frac{6}{6}\) = \(\frac{12}{54}\)
\(\frac{9}{54}\) < \(\frac{12}{54}\)
c. \(\frac{7}{12}\) and \(\frac{5}{8}\)
Answer:
\(\frac{7}{12}\) and \(\frac{5}{8}\)
\(\frac{7}{12}\) × \(\frac{8}{8}\) = \(\frac{56}{96}\)
\(\frac{5}{8}\) × \(\frac{12}{12}\) = \(\frac{60}{96}\)
\(\frac{56}{96}\) < \(\frac{60}{96}\)
Solve the story problems below. Show your work using numbers, sketches, or words.
Question 3.
Matthew read \(\frac{2}{3}\) of a book. Craig read \(\frac{4}{5}\) of the same book. Who read more? How much more?
Answer:
Matthew read \(\frac{2}{3}\) of a book.
Craig read \(\frac{4}{5}\) of the same book.
\(\frac{2}{3}\) × \(\frac{5}{5}\) = \(\frac{10}{15}\)
\(\frac{4}{5}\) × \(\frac{3}{3}\) = \(\frac{12}{15}\)
Craig read more than Matthew.
\(\frac{12}{15}\) – \(\frac{10}{15}\) = \(\frac{2}{15}\)
Craig read \(\frac{2}{15}\) than Matthew.
Question 4.
Carlos had two extra sandwiches. They were exactly the same size. He gave \(\frac{7}{9}\) of the first sandwich to his friend Ben and \(\frac{4}{6}\) of the second sandwich to his friend Corey.
a Whose piece is bigger, Corey’s or Ben’s?
Answer:
Given,
Carlos had two extra sandwiches. They were exactly the same size.
He gave \(\frac{7}{9}\) of the first sandwich to his friend Ben and \(\frac{4}{6}\) of the second sandwich to his friend Corey.
\(\frac{7}{9}\) × \(\frac{6}{6}\) = \(\frac{42}{54}\)
\(\frac{4}{6}\) × \(\frac{9}{9}\) = \(\frac{36}{54}\)
\(\frac{42}{54}\) > \(\frac{36}{54}\)
Ben’s piece is bigger than Corey’s.
b. CHALLENGE If Carlos ate the remaining pieces of the two sandwiches, did he get more or less than Corey? Did he get more or less than Ben?
Answer:
Carlos had two extra sandwiches. They were exactly the same size. He gave \(\frac{7}{9}\) of the first sandwich to his friend Ben and \(\frac{4}{6}\) of the second sandwich to his friend Corey.
1 – \(\frac{7}{9}\) = \(\frac{2}{9}\)
1 – \(\frac{4}{6}\) = \(\frac{2}{6}\)
\(\frac{2}{9}\) × \(\frac{6}{6}\) = \(\frac{12}{54}\)
\(\frac{2}{6}\) × \(\frac{9}{9}\) = \(\frac{18}{54}\)
Corey gets less than Ben.
Bridges in Mathematics Grade 5 Home Connections Unit 2 Module 4 Session 3 Answer Key
Working with Fractions
Which is greater, \(\frac{2}{3}\) or \(\frac{4}{5}\) ? Exactly how much difference is there between these two fractions? If you want to compare, add, or subtract two fractions, rewrite them so they both have the same denominator. To do this:
- Find the least common multiple of the denominators of the fractions.
multiples of 3 3, 6, 9, 12, 15
multiples of 5 5, 10, 15
The least common multiple of 3 and 5 is 15. - Multiply the numerator and denominator of each fraction by the same number so the denominators are equal.
\(\frac{2 \times 5}{3 \times 5}\) = \(\frac{10}{15}\) \(\frac{4 \times 3}{5 \times 3}\) = \(\frac{12}{15}\) \(\frac{4}{5}\) is greater than \(\frac{2}{3}\) by exactly \(\frac{2}{15}\)
Question 1.
Find the least common multiple (LCM) of each pair of numbers.
ex 4 and 10
4, 8, 12, 16, 20
10, 20
20 is the LCM of 4 and 10
a. 5 and 6
Answer:
5: 5, 10, 15, 20, 25, 30, 35
6: 6, 12, 18, 24, 30, 36
30 is the LCM of 5 and 6.
b. 2 and 7
Answer:
2: 2, 4, 6, 8, 10, 12, 14, 16, 18
7: 7, 14, 21, 28
14 is the LCM of 2 and 7.
Question 2.
Add or subtract the fractions by rewriting them so they have common denominators. Hint: Use the information from problem 1 to help.
ex \(\frac{3}{4}\) – \(\frac{7}{10}\) =
\(\frac{3 \times 5}{4 \times 5}\) = \(\frac{15}{10}\) \(\frac{7 \times 2}{10 \times 2}\) = \(\frac{14}{20}\)
\(\frac{15}{20}\) – \(\frac{14}{20}\) = \(\frac{1}{20}\)
a.
\(\frac{4}{5}\) + \(\frac{5}{6}\)
Answer:
\(\frac{4}{5}\) + \(\frac{5}{6}\)
The denominators of the fractions are not the same so find the LCD of the fractions and add them.
LCD is 30.
\(\frac{24}{30}\) + \(\frac{20}{30}\) = \(\frac{24+20}{30}\) = \(\frac{44}{30}\) = \(\frac{22}{15}\) = 1\(\frac{7}{15}\)
b.
\(\frac{4}{7}\) – \(\frac{1}{2}\)
Answer:
\(\frac{4}{7}\) – \(\frac{1}{2}\)
The denominators of the fractions are not the same so find the LCD of the fractions and subtract them.
LCD is 14
\(\frac{8}{14}\) – \(\frac{7}{14}\) = \(\frac{1}{14}\)
Question 3.
Find the greatest common factor for each pair of numbers below. Use extra paper if you need more space.

Answer:
Factors of 16: 1, 2, 4, 8 and 16
Factors of 28: 1, 2, 4, 7, 14 and 28
So, the GCF of 16 and 28 is 4.
Factors of 15: 1, 3, 5 and 15
Factors of 36: 1, 2, 3, 4, 9, 12, 18 and 36
So, the GCF of 15 and 36 is 3.
Question 4.
Find the simplest form of each fraction below.
a. \(\frac{16}{28}\)
Answer:
\(\frac{16}{28}\)
\(\frac{16}{28}\) ÷ \(\frac{4}{4}\) = \(\frac{4}{7}\)
b. \(\frac{4}{48}\)
Answer:
\(\frac{4}{48}\)
\(\frac{4}{48}\) ÷ \(\frac{4}{4}\) = \(\frac{1}{12}\)
c. \(\frac{2}{14}\)
Answer:
\(\frac{2}{14}\)
\(\frac{2}{14}\) ÷ \(\frac{2}{2}\) = \(\frac{1}{7}\)
d. \(\frac{28}{16}\)
Answer:
\(\frac{28}{16}\)
\(\frac{28}{16}\) ÷ \(\frac{4}{4}\) = \(\frac{7}{4}\) = 1\(\frac{3}{4}\)
e. \(\frac{15}{36}\)
Answer:
\(\frac{15}{36}\)
\(\frac{15}{36}\) ÷ \(\frac{3}{3}\) = \(\frac{5}{12}\)
f. \(\frac{56}{42}\)
Answer:
\(\frac{56}{42}\)
\(\frac{56}{42}\) ÷ \(\frac{14}{14}\) = \(\frac{4}{3}\) = 1\(\frac{1}{3}\)
Question 5.
Add or subtract. Show your work. Hint: Use the information in problem 4 above to help.
a. \(\frac{16}{28}\) + \(\frac{2}{14}\)
Answer:
\(\frac{16}{28}\) + \(\frac{2}{14}\)
LCD is 28.
\(\frac{16}{28}\) + \(\frac{4}{28}\) = \(\frac{16+4}{28}\) = \(\frac{20}{28}\) = \(\frac{5}{7}\)
b. \(\frac{15}{36}\) + \(\frac{4}{48}\)
Answer:
Given,
\(\frac{15}{36}\) + \(\frac{4}{48}\)
LCD is 144
\(\frac{60}{144}\) + \(\frac{12}{144}\) = \(\frac{60+12}{144}\) = \(\frac{72}{144}\) = \(\frac{1}{2}\)
c. \(\frac{28}{16}\) + \(\frac{25}{100}\)
Answer:
\(\frac{28}{16}\) + \(\frac{25}{100}\)
LCD is 400
\(\frac{700}{400}\) + \(\frac{100}{400}\) = \(\frac{800}{400}\) = 2
Question 6.
Alicia says that the greatest common factor of 8 and 12 is 24. Do you agree or disagree? Explain.
Answer:
Given,
Alicia says that the greatest common factor of 8 and 12 is 24.
Factors of 8: 1, 2, 4 and 8.
Factors of 12: 1, 2, 3, 4, 6 and 12.
So, the greatest common factor of 8 and 12 is 4.
I disagree with Alicia.
Question 7.
Felix says that \(\frac{11}{33}\) is in simplest form. Do you agree or disagree? Explain.
Answer:
Felix says that \(\frac{11}{33}\) is in simplest form.
\(\frac{11}{33}\) = \(\frac{1}{3}\)
No, I don’t agree with Felix.
Question 8.
CHALLENGE List three examples of times when people need to add or subtract fractions in their daily lives.
Answer:
Splitting a pizza, Adding ingredients while cooking, and splitting bills are a few examples of times when people need to add or subtract fractions in their daily lives.