Students looking for the Bridges in Mathematics Grade 5 Home Connections Answer Key Unit 2 Module 1 can find a better approach to solve the problems.
Bridges in Mathematics Grade 5 Home Connections Answer Key Unit 2 Module 1
Bridges in Mathematics Grade 5 Home Connections Unit 2 Module 1 Session 2 Answer Key
Comparing Fractions
Question 1.
Color in the grid to show the fractions below. Each grid represents 1 whole.
a.
\(\frac{1}{2}\)
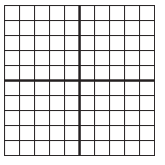
Answer:
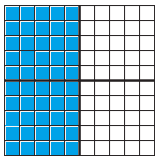
Color half of the grid to show the fraction \(\frac{1}{2}\).
b.
\(\frac{1}{4}\)
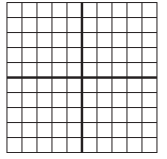
Answer:
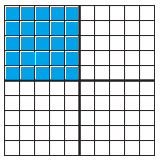
Color the quarter of the grid to show the fraction \(\frac{1}{4}\).
c.
\(\frac{3}{10}\)

Answer:

d.
\(\frac{16}{10}\)
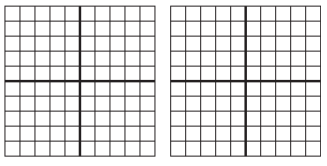
Answer:
\(\frac{16}{10}\) = \(\frac{8}{5}\)

e.
\(\frac{6}{4}\)
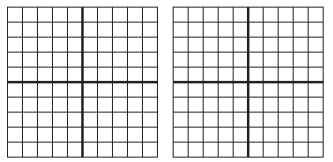
Answer:
\(\frac{6}{4}\) = \(\frac{3}{2}\) = 1 \(\frac{1}{2}\)

Question 2.
Use the pictures above to help complete each comparison below using <, >, or =.
ex \(\frac{1}{2}\) > \(\frac{3}{10}\)
a.
\(\frac{6}{4}\) 1\(\frac{1}{2}\)
Answer:
From the above figure we can say that,

\(\frac{6}{4}\) = 1\(\frac{1}{2}\)
b.
\(\frac{6}{10}\) \(\frac{3}{4}\)
Answer:
\(\frac{6}{10}\) = 0.6
\(\frac{3}{4}\) = 0.75
\(\frac{6}{10}\) < \(\frac{3}{4}\)
c.
\(\frac{16}{10}\) 1\(\frac{1}{2}\)
Answer:
\(\frac{16}{10}\) = 1\(\frac{6}{10}\)
1\(\frac{1}{2}\)
1\(\frac{6}{10}\) > 1\(\frac{1}{2}\)
\(\frac{16}{10}\) > 1\(\frac{1}{2}\)
d.
\(\frac{6}{10}\) \(\frac{6}{4}\)
Answer:
\(\frac{6}{10}\) = 0.6
\(\frac{6}{4}\) = 1\(\frac{1}{2}\)
0.6 < 1\(\frac{1}{2}\)
\(\frac{6}{10}\) < \(\frac{6}{4}\)
e.
\(\frac{3}{10}\) \(\frac{1}{4}\)
Answer:
\(\frac{3}{10}\) = 0.3
\(\frac{1}{4}\) = 0.25
0.3 > 0.25
\(\frac{3}{10}\) > \(\frac{1}{4}\)
Question 3.
Add these fractions. (Hint: Think about money to help.)
a.
\(\frac{1}{2}\) + \(\frac{1}{4}\) = __________
Answer:
\(\frac{1}{2}\) + \(\frac{1}{4}\)
LCD of 2, 4 = 4
\(\frac{2}{4}\) + \(\frac{1}{4}\) = \(\frac{2+1}{2}\) = \(\frac{3}{4}\)
b.
1\(\frac{1}{2}\) + \(\frac{3}{4}\) = __________
Answer:
1\(\frac{1}{2}\) + \(\frac{3}{4}\)
1\(\frac{1}{2}\) = \(\frac{3}{2}\)
\(\frac{3}{2}\) + \(\frac{3}{4}\)
LCD of 2, 4 = 4
\(\frac{6}{4}\) + \(\frac{3}{4}\) = \(\frac{6+3}{4}\) = \(\frac{9}{4}\)
c.
\(\frac{1}{2}\) + \(\frac{1}{10}\) = __________
Answer:
\(\frac{1}{2}\) + \(\frac{1}{10}\)
LCD of 2, 10 is 10.
\(\frac{5}{10}\) + \(\frac{1}{10}\) = \(\frac{5+1}{10}\) = \(\frac{6}{10}\) = \(\frac{3}{5}\)
d.
\(\frac{3}{10}\) + \(\frac{1}{4}\) = __________
Answer:
\(\frac{3}{10}\) + \(\frac{1}{4}\)
LCD of 4, 10 is 20.
\(\frac{6}{20}\) + \(\frac{5}{20}\) = \(\frac{6+5}{20}\) = \(\frac{11}{20}\)
Question 4.
Francisco and his mother bought some fruit yesterday. They bought 2 \(\frac{1}{2}\) pounds of peaches, \(\frac{7}{10}\) of a pound of raspberries, and 1 \(\frac{1}{4}\) pounds of apricots. How many pounds of fruit did they buy in all? Show all your work.
Answer:
Given,
Francisco and his mother bought some fruit yesterday. They bought 2 \(\frac{1}{2}\) pounds of peaches, \(\frac{7}{10}\) of a pound of raspberries, and 1 \(\frac{1}{4}\) pounds of apricots.
2 \(\frac{1}{2}\) + \(\frac{7}{10}\) + 1 \(\frac{1}{4}\)
Convert from mixed fraction to the improper fraction.
2 \(\frac{1}{2}\) = \(\frac{5}{2}\)
1 \(\frac{1}{4}\) = \(\frac{5}{4}\)
\(\frac{5}{2}\) + \(\frac{5}{4}\)
LCD of 2, 4 = 4
\(\frac{10}{4}\) + \(\frac{5}{4}\) = \(\frac{10+5}{2}\) = \(\frac{15}{4}\)
Question 5.
CHALLENGE Write three fraction addition problems in which the fractions have different denominators and the sum is 1.
ex \(\frac{1}{2}\) + \(\frac{2}{4}\) = 1
a
b
c
Answer:
\(\frac{1}{2}\) + \(\frac{2}{4}\) = 1
\(\frac{3}{8}\) + \(\frac{5}{8}\) = 1
\(\frac{2}{5}\) + \(\frac{3}{5}\) = 1
\(\frac{1}{4}\) + \(\frac{3}{4}\) = 1
Question 6.
CHALLENGE Fill in the missing numerators and denominators to make each comparison true.
a.
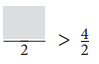
Answer:
\(\frac{4}{2}\) = 2
The denominator of the given fractions are same. So, the numerator should be greater than 4.
So, the missing number is 5.
\(\frac{5}{2}\) > \(\frac{4}{2}\)
b.
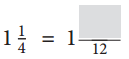
Answer:
Given,
1\(\frac{1}{4}\)
\(\frac{1}{4}\) can be written as \(\frac{3}{12}\)
1\(\frac{1}{4}\) = 1\(\frac{3}{12}\)
c.
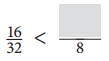
Answer:
\(\frac{16}{32}\) = \(\frac{1}{2}\)
\(\frac{3}{8}\)
\(\frac{1}{2}\) < \(\frac{3}{8}\)
\(\frac{16}{32}\) < \(\frac{3}{8}\)
Bridges in Mathematics Grade 5 Home Connections Unit 2 Module 1 Session 4 Answer Key
More Adding Fractions
Question 1.
Show the fractions on the strips or clocks. Then add them and report the sum.
Answer:
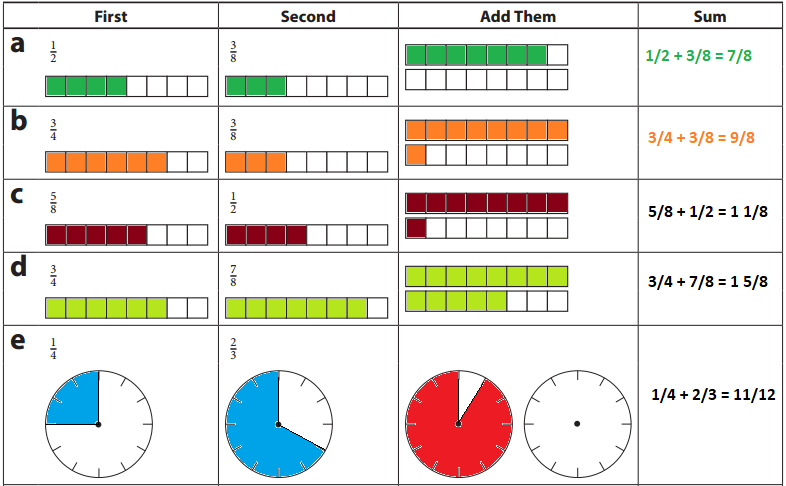
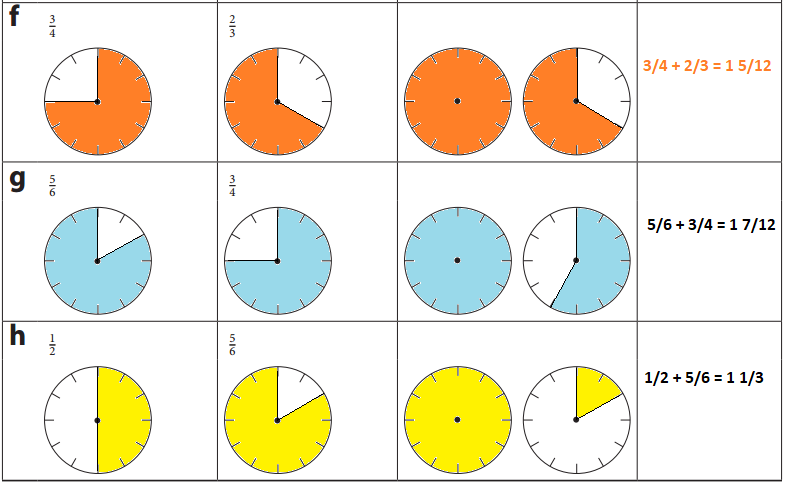
\(\frac{1}{2}\) + \(\frac{3}{8}\) = \(\frac{7}{8}\)
\(\frac{3}{4}\) + \(\frac{3}{8}\) = \(\frac{9}{8}\)
\(\frac{5}{8}\) + \(\frac{1}{2}\) = 1 \(\frac{1}{8}\)
\(\frac{3}{4}\) + \(\frac{7}{8}\) = 1 \(\frac{5}{8}\)
\(\frac{1}{4}\) + \(\frac{2}{3}\) = \(\frac{11}{12}\)
\(\frac{3}{4}\) + \(\frac{2}{3}\)
LCD is 12
\(\frac{9}{12}\) + \(\frac{8}{12}\) = \(\frac{17}{12}\)
\(\frac{1}{2}\) + \(\frac{5}{6}\) = 1 \(\frac{1}{3}\)
Show your work for each problem using numbers, sketches, or words.
Question 2.
Abby and Lauren are preparing for a dance performance. On Monday, they practiced for \(\frac{2}{3}\) of an hour. On Tuesday, they practiced for \(\frac{5}{6}\) of an hour. How long did they practice on Monday and Tuesday together?
Answer:
Given,
Abby and Lauren are preparing for a dance performance.
On Monday, they practiced for \(\frac{2}{3}\) of an hour.
On Tuesday, they practiced for \(\frac{5}{6}\) of an hour.
\(\frac{2}{3}\) + \(\frac{5}{6}\)
LCD of 3, 6 is 6.
\(\frac{4}{6}\) + \(\frac{5}{6}\) = \(\frac{4+5}{6}\) = \(\frac{9}{6}\) = 3 hours
Question 3.
On Wednesday, Abby and Lauren could not practice together, so they practiced separately. Abby practiced for \(\frac{11}{12}\) of an hour and Lauren practiced for \(\frac{2}{3}\) of an hour. How long did they practice on Wednesday?
Answer:
Given,
On Wednesday, Abby and Lauren could not practice together, so they practiced separately.
Abby practiced for \(\frac{11}{12}\) of an hour and Lauren practiced for \(\frac{2}{3}\) of an hour.
\(\frac{11}{12}\) + \(\frac{2}{3}\)
LCD is 12
\(\frac{11}{12}\) + \(\frac{8}{12}\) = \(\frac{11+8}{12}\) = \(\frac{19}{12}\)
Question 4.
CHALLENGE If you are adding two fractions that are both greater than \(\frac{1}{2}\), what must be true about the sum? Give three examples to support your thinking.
The sum must be:
Answer:
\(\frac{1}{2}\) + \(\frac{1}{4}\) = \(\frac{3}{4}\)
\(\frac{3}{4}\) is greater than \(\frac{1}{2}\)
Question 5.
CHALLENGE If you are adding two fractions that are both less than \(\frac{1}{2}\), what must be true about the sum? Give three examples to support your thinking.
The sum must be:
Answer:
\(\frac{1}{3}\) + \(\frac{1}{3}\) = \(\frac{2}{3}\)
\(\frac{2}{3}\) is less than \(\frac{1}{2}\)